Gọi I là trung điểm của EF. Trên tia đối của tia IA lấy điểm K sao cho IK = IA
20
18/08/2024
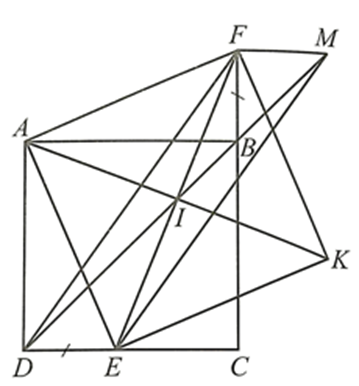
Cho hình vuông ABCD. Lấy điểm E thuộc cạnh CD và điểm F thuộc tia đối của tia BC sao cho BF = DE.
Gọi I là trung điểm của EF. Trên tia đối của tia IA lấy điểm K sao cho IK = IA. Chứng minh tứ giác AEKF là hình vuông.
Trả lời
Do IK = IA nên I là trung điểm của AK.
Tứ giác AEKF có hai đường chéo AK, EF cắt nhau tại trung điểm I của mỗi đường nên AEKF là hình bình hành.
Hình bình hành AEKF có \(\widehat {EAF} = 90^\circ \) nên AEKF là hình chữ nhật.
Hình chữ nhật AEKF có AE = AF nên AEKF là hình vuông.