Cho tam giác ABC có các đường trung tuyến BD, CE cắt nhau tại G. Gọi F, H lần lượt là trung điểm của BG, CG.

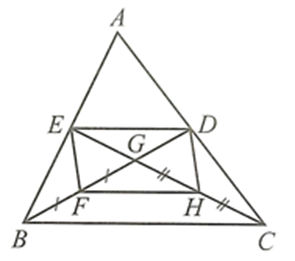
Để hình bình hành EFHD là hình vuông thì EH = DF và EH ⊥ DF.

Suy ra BG = CG, EG = DG và BD ⊥ CE.

Xét ∆BEG và ∆CDG có:

BG = CG, \(\widehat {EGB} = \widehat {DGC}\)(đối đỉnh), EG = DG

Do đó ∆BEG = ∆CDG (c.g.c). Suy ra BE = CD (hai cạnh tương ứng) (1)

Mà BD, CE là các đường trung tuyến của ∆ABC nên E là trung điểm của AB, D là trung điểm của AC

Suy ra AB = 2BE, AC = 2CD (2)

Từ (1) và (2) suy ra AB = AC

Dễ thấy, nếu AB = AC và BD ⊥ CE thì tứ giác EFHD là hình vuông.

Vậy tam giác ABC cân tại A có hai đường trung tuyến BD, CE vuông góc với nhau thì tứ giác EFHD là hình vuông.