Cho hình vuông ABCD có AB = 12 cm. Trên cạnh CD lấy điểm E sao cho DE = 5 cm. Tia phân giác của góc BAE cắt BC tại F. Trên tia đối của tia BC lấy điểm M sao cho BM = DE.
Chứng minh AE = AM = FM.
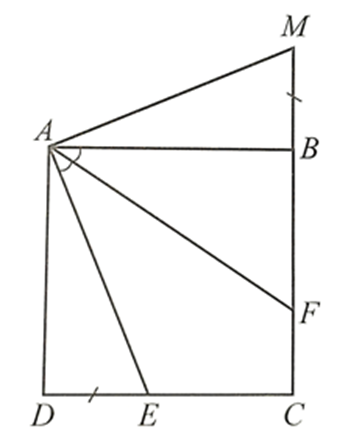
Do ABCD là hình vuông nên AB = AD, \(\widehat {ADC} = \widehat {ABC} = 90^\circ \)
Ta có: \(\widehat {ABM} + \widehat {ABC} = 180^\circ \) (2 góc kề bù) nên \(\widehat {ABM} = 180^\circ - \widehat {ABC} = 180^\circ - 90^\circ = 90^\circ \)
Xét ∆ADE và ∆ABM có:
\(\widehat {ADE} = \widehat {ABM} = 90^\circ \), AD = AB, DE = BM
Do đó ∆ADE = ∆ABM (hai cạnh góc vuông)
Suy ra AE = AM (1) và \(\widehat {DAE} = \widehat {BAM}\).
Do AF là tia phân giác của \(\widehat {BAE}\) nên \(\widehat {EAF} = \widehat {BAF}\).
Suy ra \(\widehat {DAE} + \widehat {EAF} = \widehat {BAM} + \widehat {BAF}\) hay \(\widehat {DAF} = \widehat {MAF}\).
Mà \(\widehat {DAF} = \widehat {MFA}\) (hai góc so le trong do AD // BC), suy ra \(\widehat {MFA} = \widehat {MAF}\).
Do đó, tam giác MAF cân tại M nên AM = FM (2)
Từ (1) và (2) suy ra AE = AM = FM.