Cho hình bình hành ABCD. Ở phía ngoài Chứng minh tan giác HAF = ta giác ADC
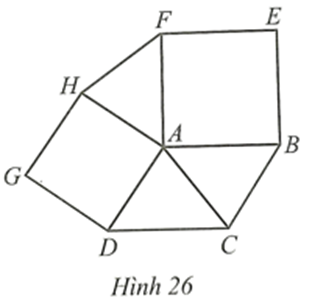
Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH (Hình 26).
Chứng minh:
DHAF = DADC.
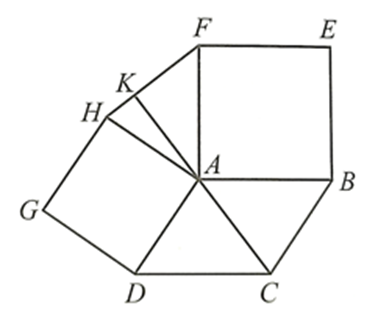
Gọi K là giao điểm của AC và HF.
Do ABEF và ADGH đều là hình vuông nên \(\widehat {BAF} = \widehat {DAH} = 90^\circ \), AF = AB, AH = AD.
Do ABCD là hình bình hành nên AB = DC
Mà AF = AB nên AF = DC.
Ta có: \(\widehat {HAF} + \widehat {FAB} + \widehat {DAB} + \widehat {DAH} = 360^\circ \)
Mà \(\widehat {BAF} = \widehat {DAH} = 90^\circ \) nên \(\widehat {HAF} + \widehat {DAB} = 360^\circ - \left( {90^\circ + 90^\circ } \right) = 180^\circ \) (1)
Hình bình hành ABCD có AB // DC nên \(\widehat {ADC} + \widehat {DAB} = 180^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {HAF} = \widehat {ADC}\).
Xét ∆HAF và ∆ADC có:
AH = AD, \(\widehat {HAF} = \widehat {ADC}\), AF = DC
Suy ra DHAF = DADC (c.g.c).