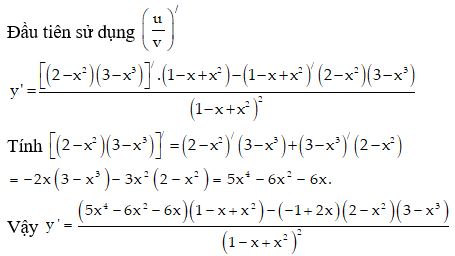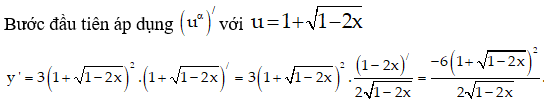20 câu hỏi trắc nghiệm thuộc 100 câu trắc nghiệm Đạo hàm nâng cao (P1)

100 câu trắc nghiệm Đạo hàm nâng cao

100 câu trắc nghiệm Đạo hàm nâng cao (P1)

619 lượt thi
20 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Tính đạo hàm của hàm số sau $y = \frac{1 + x - x^{2}}{1 - x + x^{2}}$

A.

B.

C.

D.

Chọn B.

Câu 2:

Tính đạo hàm của hàm số sau: y = (x² – x + 1)³.(x² + x + 1)²

A: (x² – x + 1)²(x² + x + 1)

B: (x² – x + 1)²(x² + x + 1)[(2x + 3)(x + x²)]

C: (x² – x + 1)²(x² + x + 1)[3(2x - 1) + 2(2x + 1)]

D: Tất cả sai

Chọn D.

Đầu tiên sử dụng quy tắc nhân.

y’ = [(x² – x + 1)]’(x² + x + 1)² + [(x²x + 1)²]/(x² – x + 1)³.

Sau đó sử dụng công thức $(u^{a})'$

y' = 3(x² – x + 1)²(x² – x + 1)’(x² + x + 1) + 2(x² + x + 1)(x² + x + 1)’(x² – x + 1)³

y’ = 3(x² – x + 1)²(2x – 1) (x² + x + 1)² + 2(x² + x + 1)(2x + 1)(x² – x + 1)³

y’ = (x² – x + 1)²(x² + x + 1)[3(2x – 1)(x² + x + 1) + 2(2x + 1)(x² – x + 1)].

Câu 3:

Tính đạo hàm của hàm số sau: $y = {(\frac{2 x + 1}{x - 1})}^{3}$

A.

B.

C.

D.

Chọn A.

Câu 4:

Tính đạo hàm của hàm số sau: $y = \frac{1}{{(x^{2} - x + 1)}^{5}}$

A.

B.

C.

D: Tất cả sai

Chọn D.

Câu 5:

Tính đạo hàm của hàm số sau: $y = \frac{(2 - x^{2}) (3 - x^{3})}{1 - x + x^{2}}$

A.

B.

D: Tất cả sai.

Chọn A.

Câu 6:

Đạo hàm của hàm số sau là đa thức bậc mấy: y = (1 + 2x)(2 + 3x²)(3 – 4x³).

A: 3

B: 4

C: 5

D: 6

Chọn C.

y' = (1 + 2x)’(2 + 3x²)(3 – 4x³) + (1 + 2x)(2 + 3x²)’(3 – 4x³) + (1 + 2x)(2 + 3x²)(3 – 4x³)’

y’ = 2(2 + 3x²)(3 – 4x³) + (1 + 2x)(6x)(3 – 4x³) + (1 + 2x)(2 + 3x²)(-12x²).

Rút gọn ta được đa thức bậc 5.

Câu 7:

Tính đạo hàm của hàm số sau: $y = \sqrt{x - 1} + \frac{1}{\sqrt{x - 1}}$

A.

B.

C.

D.

Chọn C.

Câu 8:

Tính đạo hàm của hàm số sau: $y = {(\sqrt{x} - \frac{1}{\sqrt{x}})}^{5}$

A.

B.

C.

D: Tất cả sai

Chọn C.

Câu 9:

Tính đạo hàm của hàm số sau: $y = \sqrt{x + \sqrt{x + \sqrt{x}}}$

A.

B. $\frac{1}{2 \sqrt{x \sqrt{x \sqrt{x}}}} (1 + \frac{1}{2 \sqrt{x}})$

C.

D. $\frac{1}{2 \sqrt{x \sqrt{x \sqrt{x}}}} (1 + \frac{1}{2 \sqrt{x}}) (1 + x)$

Chọn A.

Câu 10:

Tính đạo hàm của hàm số sau: $y = \frac{4 x + 1}{\sqrt{x^{2} + 2}}$

A.

B.

C.

D.

Chọn C.

Câu 11:

Tính đạo hàm của hàm số sau $y = {(1 + \sqrt{1 - 2 x})}^{3}$

A.

B.

C.

D.

Chọn C.

Câu 12:

Cho hàm số f(x) xác định bởi $f (x) = \{\begin{cases} \frac{\sqrt{x^{2} + 1} - x}{x} (x \neq 0) \\ 0 (x = 0) \end{cases}$ . Giá trị f’(0) bằng:

A. 0

B. 1

C. 1/2.

D. Không tồn tại.

Chọn C.

Câu 13:

Cho hàm số $f (x) = \frac{3 x^{2} + 2 x + 1}{2 \sqrt{3 x^{3} + 2 x^{2} + 1}}$ . Giá trị f’(0) là:

A. 0.

B. 1/2

C. Không tồn tại.

D. 1.

Chọn B.

Câu 14:

Tính đạo hàm của hàm số sau: y = (x² – x + 1)³ .(x² + x + 1)²

A. y’ = (x² – x + 1)²[3(2x – 1)(x² + x + 1) + 2(2x + 1)(x² – x + 1)]

B. y’ = (x² – x + 1)²(x² + x + 1)[3(2x – 1)(x² + x + 1) + (x² – x + 1)]

C. y’ = (x² – x + 1)²(x² + x + 1)[3(2x – 1)(x² + x + 1) + 2(2x + 1)(x² – x + 1)]

D. y’ = (x² – x + 1)²(x² + x + 1)[3(2x – 1)(x² + x + 1) – 2(2x + 1)(x² – x + 1)]

Chọn C.

Đầu tiên sử dụng quy tắc nhân.

y' = [(x² – x + 1)³]’(x² + x + 1)² + [(x² + x + 1)²]’(x² – x + 1)³.

Sau đó sử dụng công thức

y' = 3(x² – x + 1)²(x² – x + 1)’(x² + x + 1) + 2(x² + x + 1)(x² + x + 1)’(x² – x + 1)³

y’ = 3(x² – x + 1)²(2x – 1)(x² + x + 1)² + 2(x² + x + 1)(2x + 1)(x² – x + 1)³

y’ = (x² – x + 1)²(x² + x + 1)[3(2x – 1)(x² + x + 1) + 2(2x + 1)(x² – x + 1)].

Câu 15:

Tính đạo hàm của hàm số $y = \sqrt{\frac{x^{3}}{x - 1}}$ (Áp dụng căn bặc hai của u đạo hàm).

A.

B.

C.

D.

Chọn D.

Câu 16:

Tính đạo hàm của hàm số $y = \sqrt{\sqrt{x^{2} + 1} + 2 x - 1}$

A.

B.

C.

D.

Chọn D.

Câu 17:

Cho hàm số $y = f (x) = \{\begin{cases} x^{2} k h i x \geq 1 \\ 2 x - 1 k h i x < 1 \end{cases}$ . Hãy chọn câu sai:

A. f’(1) = 1.

B. Hàm số có đạo hàm tại x_o=1.

C. Hàm số liên tục tại x_o = 1.

D. $f' (x) = \{\begin{cases} 2 x k h i x \geq 1 \\ 2 k h i x < 1 \end{cases}$

Chọn A.

Câu 18:

Tính đạo hàm của hàm số $f (x) = \{\begin{cases} x^{2} + x + 1 k h i x < 1 \\ \sqrt{x - 1} + 3 k h i x > 1 \end{cases}$

A.

B.

C.

D.

Chọn D.

Câu 19:

Tìm a; b để các hàm số sau có đạo hàm trên R. $f (x) = \{\begin{cases} x^{2} - x + 1 k h i x \leq 1 \\ - x^{2} + a x + b k h i x > 1 \end{cases}$

A. $\{\begin{cases} a = 13 \\ b = - 1 \end{cases}$

B. $\{\begin{cases} a = 3 \\ b = - 11 \end{cases}$

C. $\{\begin{cases} a = 23 \\ b = - 21 \end{cases}$

D. $\{\begin{cases} a = 3 \\ b = - 1 \end{cases}$

Chọn D.

Câu 20:

Tìm x thoả mãn 2xf’(x) – f(x) ≥ 0 với $f (x) = x + \sqrt{x^{2} + 1}$

A.

B.

C.

D.

Chọn A.

Bắt đầu thi ngay

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương