Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA =  . Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy

Bài 5 trang 62 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = $a\sqrt{3}$ . Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Gọi (a) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).

a) Tìm các giao tuyến của mặt phẳng (a) với các mặt của hình chóp.

b) Các giao tuyến ở câu a tạo thành hình gì? Tính diện tích của hình đó.

Trả lời

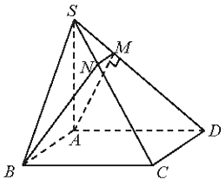
a) Ta có:

(SAB) ⊥ (ABCD);

(SAD) ⊥ (ABCD);

Do đó SA ⊥ (ABCD).

(SAB) $\cap$ (SAD) = SA.

Dễ dàng chứng minh được (SAD) ⊥ (SCD).

Vẽ AM ⊥ SD (M $\in$ SD) $\Rightarrow$ AM ⊥ (SCD)

Do đó (ABM) ⊥ (SCD) hay (ABM) là mặt phẳng (α) qua AB và vuông góc với mặt phẳng (SCD).

Trong mặt phẳng (SCD) kẻ MN // CD (N$\in$ SC).

Suy ra: MN // AB$\Rightarrow$ MN $\subset$ (α).

Vậy các giao tuyến của (α) với các mặt của hình chóp là AB, BN, NM, MA.

b)

Ta có: MN // AB;AB ⊥ AM (vì AB ⊥ (SAD)).

Suy ra ABNM là hình thang vuông tại A và M.

Tam giác SAD vuông tại A có AM là đường cao nên:

$\frac{1}{A{M}^2}=\frac{1}{S{A}^2}+\frac{1}{A{D}^2}=\frac{1}{3a^2}+\frac{1}{a^2}=\frac{4}{3a^2}\Rightarrow AM=\frac{a\sqrt{3}}{2}.$

Vì MN // CD nên $\frac{MN}{CD}=\frac{SM}{SD}$

$\Rightarrow \frac{MN}{CD}=\frac{S{A}^2}{SD}\cdot \frac{1}{SD}=\frac{S{A}^2}{S{D}^2}=\frac{S{A}^2}{S{A}^2+A{D}^2}=\frac{3a^2}{4a^2}$

$\Rightarrow MN=\frac{3}{4}CD=\frac{3}{4}a$

$\Rightarrow S_{ABMN}=\frac{1}{2}.AM.(MN+AB)=\frac{1}{2}.\frac{a\sqrt{3}}{2}.\left(\frac{3}{4}a+a\right)=\frac{7a^2\sqrt{3}}{16}$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Hai mặt phẳng vuông góc

Bài 4: Khoảng cách trong không gian

Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài tập cuối chương 8