Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA ⊥ (ABC). Chứng minh rằng (SBC) ⊥ (SAB)

Bài 3 trang 61 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B và SA ⊥ (ABC).

a) Chứng minh rằng (SBC) ⊥ (SAB).

b) Gọi M là trung điểm của AC. Chứng minh rằng (SBM) ⊥ (SAC).

Trả lời

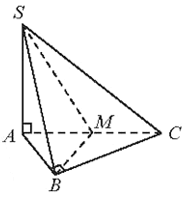
a)Ta có: BC ⊥ AB (giả thiết);

Đồng thời BC ⊥ SA (vì SA ⊥ (ABC)).

$\Rightarrow$ BC ⊥ (SAB)

$\Rightarrow$ (SBC) ⊥ (SAB).

b)Vì tam giác ABC là tam giác vuông cân tại B nên BM ⊥ AC.

Mà BM ⊥ SA (vì SA ⊥ (ABC))

$\Rightarrow$ BM ⊥ (SAC) (1)

BM $\subset$ (SBM) (2)

Từ (1) và (2) suy ra (SBM) ⊥ (SAC).

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng

Bài 3: Hai mặt phẳng vuông góc

Bài 4: Khoảng cách trong không gian

Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài tập cuối chương 8