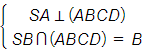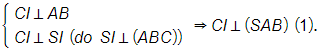Giải SBT Toán 11 (Chân trời sáng tạo) Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Sách bài tập Toán 11 Bài 5: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện

Bài 1 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là hình vuông tâm O cạnh a, SA = $a\sqrt{3}$ và vuông góc với đáy. Xác định và tính góc giữa:

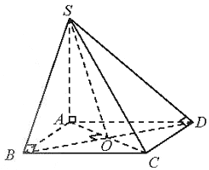
a) SB và (ABCD);

b) SC và (ABCD);

c) SD và (ABCD);

d) SB và (SAC).

Lời giải:

a) Ta có: 

Suy ra AB là hình chiếu của SB trên (ABCD).

Do đó (SB, (ABCD)) = (SB, AB).

Trong tam giác SAB vuông tại A, ta có:

$\tan \widehat{SBA}=\frac{SA}{AB}=\sqrt{3}\Rightarrow \widehat{SBA}=60°.$

Vậy $(SB,(ABCD\left)\right)=\widehat{SBA}=60°.$

b) Tương tự câu a) ta xác định được (SC, (ABCD)) = (SC, AC).

Trong tam giác SAC vuông tại A, ta có:

$\tan \widehat{SCA}=\frac{SA}{AC}=\frac{\sqrt{3}}{\sqrt{2}}\Rightarrow \widehat{SCA}\approx \mathrm{50,8}°.$

Vậy $(SC,(ABCD\left)\right)=\widehat{SCA}\approx \mathrm{50,8}°.$

c) Tương tự câu a) ta xác định được (SD, (ABCD)) = (SD,AD).

Trong tam giác SAD vuông tại A, ta có:

$\tan \widehat{SDA}=\frac{SA}{AD}=\sqrt{3}\Rightarrow \widehat{SDA}=60°.$

Vậy $(SD,(ABCD\left)\right)=\widehat{SDA}=60°.$

d) Ta có: 

$\Rightarrow$ BD ⊥ (SAC) hay BO ⊥ (SAC). (1)

Mà SB $\cap$ (SAC) = S. (2)

Từ (1) và (2) suy ra SO là hình chiếu của SB trên (SAC).

Do đó: (SB, (SAC))=(SB, SO).

Trong tam giác SBO vuông tại O, ta có:

$BO=\frac{1}{2}BD=\frac{a\sqrt{2}}{2},SB=2a.$

$\Rightarrow \sin \widehat{BSO}=\frac{BO}{SB}=\frac{\sqrt{2}}{4}\Rightarrow \widehat{BSO}\approx \mathrm{20,7}°.$

Vậy $(SB,(SAC\left)\right)=\widehat{BSO}\approx \mathrm{20,7}°.$

Bài 2 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 3. Hình chiếu vuông góc của S trên mặt phẳng đáy trùng với trung điểm I của cạnh AB. Biết rằng mặt bên (SAB) là tam giác vuông cân tại S. Xác định và tính góc giữa:

a) SA và (ABC);

b) SC và (SAB).

Lời giải:

a)Vì AI là hình chiếu của SA trên (ABC).

Do đó (SA, (ABC)) = (SA, AI).

Vì tam giác SAI vuông cân tại I $\Rightarrow \widehat{SAI}=45°.$

Vậy $(SA,(ABC\left)\right)=(SA,AI)=\widehat{SAI}=45°$ .

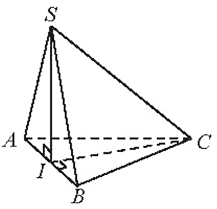
b)Ta có tam giác ABC đều nên CI ⊥ AB, $CI=\frac{3\sqrt{3}}{2}.$

Ta có: 

Mà SC $\cap$ (SAB) = S. (2)

Từ (1) và (2) $\Rightarrow$ SI là hình chiếu của SC trên (SAB).

Do đó (SC, (SAB)) = (SC, SI).

Trong tam giác SAB vuông tại S, $SI=\frac{1}{2}AB=\frac{3}{2}$ .

Trong tam giác SCI vuông tại I, ta có $\tan \widehat{CSI}=\frac{IC}{SI}=\sqrt{3}\Rightarrow \widehat{CSI}=60°.$

Vậy $\left(SC,\left(SAB\right)\right)=\widehat{CSI}=60°.$

Bài 3 trang 73 SBT Toán 11 Tập 2: Cho hình chóp tam giác đều S.ABC, cạnh đáy bằng a, cạnh bên bằng $\frac{a\sqrt{15}}{6}$ . Tính số đo góc phẳng nhị diện [S, BC, A].

Lời giải:

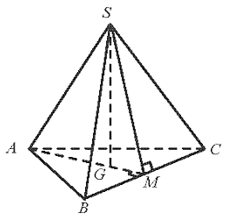
Gọi M là trung điểm BC, G là trọng tâm tam giác ABC.

Ta có SG ⊥ (ABC), SM ⊥ BC, AM ⊥ BC.

Suy ra $\widehat{SMG}$ là góc phẳng nhị diện [S, BC, A].

Ta tính được

$AM=\frac{a\sqrt{3}}{2}\Rightarrow GM=\frac{AM}{3}=\frac{a\sqrt{3}}{6},$

$SM=\sqrt{S{B}^2-B{M}^2}=\frac{a\sqrt{6}}{6},$

$SG=\sqrt{S{M}^2-G{M}^2}=\frac{a\sqrt{3}}{6}.$

$\Rightarrow$ GM = SG.

Ta có tam giác SMG vuông cân tại G, suy ra số đo góc phẳng nhị diện [S, BC, A] = $\widehat{SMG}=45°.$

Bài 4 trang 73 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Tam giác ABC vuông tại A, $\widehat{AB\text{}C}=30°$, AC = a, $SA=\frac{a\sqrt{3}}{2}$. Tính số đo góc phẳng nhị diện [S, BC, A].

Lời giải:

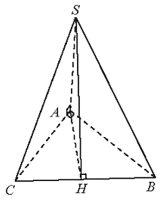
Vẽ AH ⊥ BC (H ϵ BC), ta có SH ⊥ BC.

Suy ra $\widehat{SHA}$ là góc phẳng nhị diện [S, BC, A].

Ta có AH = AC.sin60° = $\frac{a\sqrt{3}}{2}$= SA

Do đó $\widehat{SHA}$ = 45°.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác: