Cho hình chữ nhật ABCD có hai cạnh kề không bằng nhau. Tia phân giác của các góc A và B cắt nhau tại E. Tia phân giác của các góc C và D cắt nhau tại F. Gọi G là giao điểm của AE và DF, H là giao điểm của BE và CF. Chứng minh:
GH // CD;
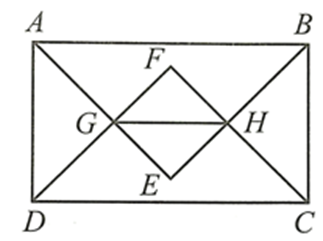
Do ABCD là hình chữ nhật nên \(\widehat {DAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDA} = 90^\circ \)
Mà AE, BE, CF, DF lần lượt là các tia phân giác của các \(\widehat {BAD},\widehat {ABC},\widehat {BCD},\widehat {ADC}\)
Suy ra \(\widehat {DAE} = \widehat {EAB} = \widehat {ABE} = \widehat {EBC} = \widehat {BCF} = \widehat {FCD} = \widehat {CDF} = \widehat {FDA} = \frac{{90^\circ }}{2} = 45^\circ {\rm{.\;}}\)
Xét ∆ADG có: \(\widehat {ADG} + \widehat {AGD} + \widehat {GAD} = 180^\circ \)
Suy ra \(\widehat {AGD} = 180^\circ - \left( {\widehat {ADG} + \widehat {GAD}} \right) = 180^\circ - \left( {45^\circ + 45^\circ } \right) = 90^\circ \)
Do đó ∆ADG vuông cân tại G
Chứng minh tương tự các tam giác EAB, FCD, HBC đều là tam giác vuông cân.
Xét ∆GAD và ∆HBC có:
\(\widehat {GAD} = \widehat {GDA} = \widehat {HBC} = \widehat {HCB} = 45^\circ \), cạnh AD = BC (do ABCD là hình chữ nhật)
Do đó ∆GAD = ∆HBC (g.c.g).
Suy ra GD = HC (hai cạnh tương ứng).
Mà FD = FC, suy ra FG = FH.
∆GFH có: \(\widehat {GFH} = 90^\circ \) và FG = FH
Do đó, tam giác FGH vuông cân tại F. Suy ra \(\widehat {FGH} = 45^\circ \).
Ta có: \(\widehat {FGH} = \widehat {CDF} = 45^\circ \) và \(\widehat {FGH},\widehat {CDF}\) nằm ở vị trí đồng vị nên GH // CD.