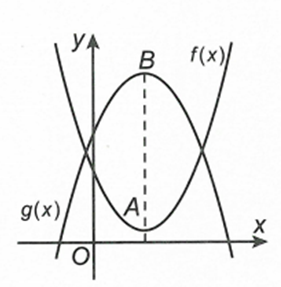
Cho hai hàm đa thức $y=f\left(x\right)$ , $y=g\left(x\right)$ có đồ thị là hai đường cong như hình vẽ. Biết rằng đồ thị hàm số $y=f\left(x\right)$  có đúng một điểm cực trị là , đồ thị hàm số $y=g\left(x\right)$  có đúng một điểm cực trị là (với $x_A=x_B$ ) và $AB=\frac{7}{2}$ . Có bao nhiêu giá trị nguyên của$m\in \left(-10;10\right)$ để hàm số $y=\left|\left|f\left(x\right)-g\left(x\right)\right|+m\right|$  có đúng bảy điểm cực trị?

Hướng dẫn giải

Gọi $x_1$ , $x_2$ với $x_1<x_2$  là hoành độ giao điểm của đồ thị $y=f\left(x\right)$  và  $y=g\left(x\right)$(dựa vào đồ thị đã cho, hai đồ thị chỉ có hai giao điểm đã kể trên, tức là

$f\left(x\right)-g\left(x\right)=0\iff \left[\begin{array}{l}x=x_1\\ x=x_2\end{array}\right.$.

Xét $h\left(x\right)=\left|f\left(x\right)-g\left(x\right)\right|+m$ .

Ta có: $h^{\text{'}}\left(x\right)=\left[f^{\text{'}}\left(x\right)-g^{\text{'}}\left(x\right)\right].\frac{f\left(x\right)-g\left(x\right)}{\left|f\left(x\right)-g\left(x\right)\right|}$ .

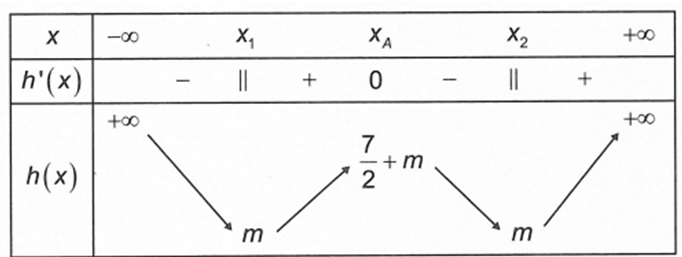
Cho $h^{\text{'}}\left(x\right)=0\iff x=x_A=x_B$  . Ta có bảng biến thiên của  như sau

            Dựa vào bảng biến thiên của $h\left(x\right)$ , yêu cầu bài toán trở thành $m<0<m+\frac{7}{2}\iff -\frac{7}{2}<m<0$ .

            Do m nguyên và  $m\in \left(-10;10\right)$nên $m\in \left\{-3;-2;-1\right\}$ .

            Chọn C.