Cho dãy số (un) có tổng n số hạng đầu là Sn = n(-1-5n)/ với n ∈ ℕ*. a) Tính u1, u2 và u3
262
18/08/2023
Bài 55 trang 57 SBT Toán 11 Tập 1: Cho dãy số (un) có tổng n số hạng đầu là Sn=n(−1−5n)2 với n ∈ ℕ*.
a) Tính u1, u2 và u3.
b) Tìm công thức của số hạng tổng quát un.
c) Chứng minh rằng dãy số (un) là một cấp số cộng.
Trả lời
a) Ta có: u1=S1=1.(−1−5.1)2=−3 .
Vì u1+u2=S2=2.(−1−5.2)2=−11 nên u2 = S2 – u1 = – 11 – (– 3) = – 8.
Vì S2+u3=S3=3(−1−5.3)2=−24 nên u3 = S3 – S2 = – 24 – (– 11) = – 13.
b) Ta có: un = Sn – Sn – 1 =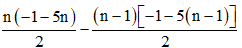
=−n−5n2−(n−1)(−1−5n+5)2=−n−5n2−(−n−5n2+5n+1+5n−5)2
=−10n+42=2−5n.
Vậy un = 2 – 5n.
c) Ta có: 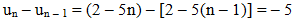 , với mọi n ≥ 2.
, với mọi n ≥ 2.
Vậy dãy số (un) là một cấp số cộng.
Xem thêm lời giải bài tập SBT Toán 11 Cánh diều hay, chi tiết khác:
Bài 2: Cấp số cộng
Bài 3: Cấp số nhân
Bài tập cuối chương 2
Bài 1: Giới hạn của dãy số
Bài 2: Giới hạn của hàm số
Bài 3: Hàm số liên tục

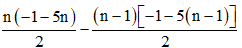
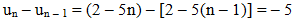 , với mọi n ≥ 2.
, với mọi n ≥ 2.