Cho các dãy số (an), (bn), (cn), (dn) được xác định như sau: +) a1 = 0; a2 = 1; a3 = 2; a4 = 3; a5 = 4

Hoạt động khám phá 3 trang 46 Toán 11 Tập 1: Cho các dãy số (a_n), (b_n), (c_n), (d_n) được xác định như sau:

+) a₁ = 0; a₂ = 1; a₃ = 2; a₄ = 3; a₅ = 4.

+) b_n = 2n.

+) 

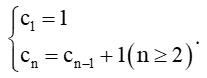
+) d_n là chu vi của đường tròn có bán kính n.

Tính bốn số hạng đầu tiên của các dãy số trên.

Trả lời

+) Bốn số hạng đầu của dãy (a_n­) là: a₁ = 0; a₂ = 1; a₃ = 2; a₄ = 3.

+) Bốn số hạng đầu của dãy (b_n­) là:

b₁ = 2.1 = 2;

b₂ = 2.2 = 4;

b₃ = 2.3 = 6;

b₄ = 2.4 = 8.

+) Bốn số hạng đầu của dãy (C_n­) là:

c₁ = 1;

c₂ = c₁ + 1 = 1 + 1 = 2;

c₃ = c₂ + 1 = 2 + 1 = 3;

c₄ = c₃ + 1 = 3 + 1 = 4.

+) d_n là chu vi của đường tròn có bán kính n được xác định bởi công thức: d_n = 2πn.

Khi đó bốn số hạng đầu của dãy (d_n­) là:

d₁ = 2π.1 = 2π;

d₂ = 2π.2 = 4π;

d₃ = 2π.3 = 6π;

d₄ = 2π.4 = 8π.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2