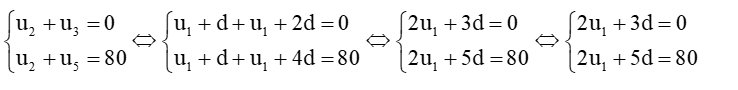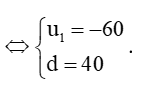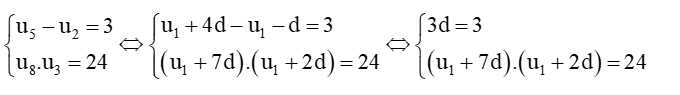Giải SGK Toán 11 (Chân trời sáng tạo) Bài 2: Cấp số cộng

Giải Toán 11 Bài 2: Cấp số cộng

Hoạt động khởi động trang 52 Toán 11 Tập 1: Một rạp hát có 20 hàng ghế. Tính từ sân khấu, số lượng ghế của các hàng tăng dần như trong hình minh họa dưới đây.

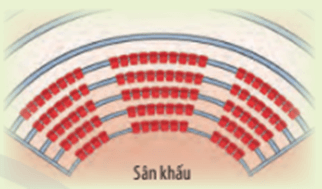
Bạn hãy đếm và nêu nhận xét về số ghế của năm hàng đầu tiên.

Làm thế nào để biết được số ghế của một hàng bất kì và tính được tổng số ghế trong rạp hát đó?

Lời giải:

Tiến hành đếm, ta có được kết quả sau:

Hàng 1: có 14 ghế;

Hàng 2: có 17 ghế;

Hàng 3: có 20 ghế;

Hàng 4: có 23 ghế;

Hàng 5: có 26 ghế.

Dựa vào số ghế của 5 hàng ghế đầu ta thấy hàng sau hơn hàng trước 3 ghế.

Sau bài học này ta biết số ghế của mỗi hàng ghế lập thành một cấp số cộng, có công thức tổng quát là: u_n = u₁ + (n – 1)d; trong đó u₁ = 14 là số ghế của hàng đầu tiên, d = 3 là công sai.

1. Cấp số cộng

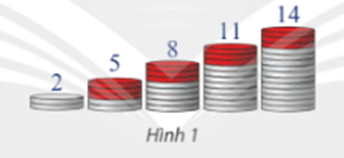
Hoạt động khám phá 1 trang 52 Toán 11 Tập 1: Tìm điểm giống nhau của các dãy số sau:

a) 2; 5; 8; 11; 14 (xem Hình 1).

b) 2; 4; 6; 8.

c) 5; 10; 15; 20; 25.

d) – 5; – 2; 1; 4; 7; 10.

Lời giải:

Nhận xét: Điểm giống nhau của các dãy số là:

Dãy số trên đều là các dãy số tăng.

Kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số d không đổi.

Thực hành 1 trang 53 Toán 11 Tập 1: Chứng minh mỗi dãy số sau là cấp số cộng. Xác định công sai của mỗi cấp số cộng đó.

a) 3; 7; 11; 15; 19; 23.

b) Dãy số (u_n) với u_n = 9n – 9.

c) Dãy số (v_n) với v_n = an + b, trong đó a và b là các hằng số.

Lời giải:

a) Dãy số 3; 7; 11; 15; 19; 23 là cấp số cộng với công sai d = 4.

b) Ta có: u₁ = 9.1 – 9 = 0.

u_n+1 = 9(n + 1) – 9 = 9n – 9 + 9 = u_n + 9, ∀n ∈ ℕ^*.

Vậy dãy số (u_n) là cấp số cộng với số hạng đầu u₁ = 0 và công sai d = – 3.

c) Ta có: v₁ = a.1 + b = a + b.

v_n+1 = a(n + 1) + b = an + a + b = an + b + a = v_n + a, ∀n ∈ ℕ^*.

Vậy dãy số (v_n) là cấp số cộng với số hạng đầu v₁ = a + b và công sai là d = a.

Thực hành 2 trang 53 Toán 11 Tập 1: Số đo ba góc của một tam giác vuông lập thành một cấp số cộng. Tìm số đo ba góc đó.

Lời giải:

Giả sử tam giác vuông thỏa mãn điều kiện bài toán là tam giác ABC vuông tại A.

Đặt $\hat{B}=\alpha ,\hat{C}=\beta ,\hat{A}=90°\left(\alpha <\beta <90°\right)$.

Ta có: α, β, 90° là một cấp số cộng nên ta có: $\beta =\frac{\alpha +90°}{2}$

Mặt khác, ta có: α + β + 90° = 180°

$\iff \alpha +\frac{\alpha +90°}{2}+90°=180°$

$\iff 3\alpha =90°$

$\iff \alpha =30°$

$\Rightarrow \beta =\frac{30°+90°}{2}=60°$.

Vậy $\hat{B}=30°,\hat{C}=60°,\hat{A}=90°$.

Vận dụng 1 trang 53 Toán 11 Tập 1: Mặt cắt của một tổ on có hình lưới tạo bởi các ô hình lục giác đều. Từ một ô đầu tiên, bước thứ nhất, các ong thợ tạo ra vòng 1 gồm 6 ô lục giác; bước thứ hai, các ong thợ sẽ tạo ra vòng 2 có 12 ô bao quanh vòng 1; bước thứ ba, các ong thợ sẽ tạo ra 18 ô bao quang vòng 2, cứ thế tiếp tục (Hình 2). Số ô trên các vòng theo thứ tự có tạo thành cấp số cộng không? Nếu có, tìm công sai của cấp số cộng này.

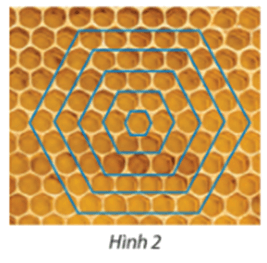
Lời giải:

Vòng 1: Có 6 ô;

Vòng 2: Có 12 ô;

Vòng 3: Có 18 ô;

...

Ta có dãy số: 6; 12; 18; ...

Từ số hạng thứ 2 trở đi số hạng sau hơn số hạng trước 6 đơn vị nên đây là một cấp số cộng có số hạng đầu là 6 và công sai là 6.

2. Số hạng tổng quát của cấp số cộng

Hoạt động khám phá 2 trang 54 Toán 11 Tập 1: Cho cấp số cộng (u_n). Hãy cho biết các hiệu số sau đây gấp bao nhiêu lần công sai d của (u_n) : u₂ – u₁; u₃ – u₁; u₄ – u₁; ...; u_n – u₁.

Lời giải:

Ta có:

u₂ – u₁ = d;

u₃ – u₁ = 2d;

u₄ – u₁ = 3d;

...

u_n – u₁ = (n – 1)d.

Thực hành 3 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của các cấp số cộng sau:

a) Cấp số cộng (a_n) có a₁ = 5 và d = – 5;

b) Cấp số cộng (b_n) có b₁ = 2 và b₁₀ = 20.

Lời giải:

a) Cấp số cộng (a_n) có a₁ = 5 và d = – 5

Số hạng tổng quát là: a_n = a₁ + (n – 1).d = 5 + (n – 1).(– 5) = 5 + – 5n + 5 = – 5n + 10.

b) Cấp số cộng (b_n) có b₁ = 2 và b₁₀ = 20.

Số hạng tổng quát là: b_n = b₁ + (n – 1)d

Khi đó b₁₀ = 2 + (10 – 1).d = 2 + 9d = 20

⇒ d = 2

Vậy số hạng tổng quát là: b_n = 2 + (n – 1).2 = 2n.

Vận dụng 2 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của cấp số cộng (c_n) có c₄ = 80 và c₆ = 40.

Lời giải:

Ta có: c₄ = c₁ + 3d = 80 và c₆ = c₁ + 5d = 40. Khi đó ta có hệ phương trình:

.

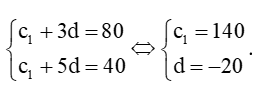
Khi đó số hạng tổng quát của cấp số cộng trên là:

c_n = 140 + (n – 1).(– 20) = – 20n +160.

Vậy số hạng tổng quát của cấp số cộng (c_n) là: c_n = – 20n + 160.

3. Tổng của n số hạng đầu tiên của cấp số cộng

Hoạt động khám phá 3 trang 54 Toán 11 Tập 1: Cho cấp số cộng (u_n) có công sai d.

a) Tính các tổng u_n + u₁; u₂ + u_n-1; u₃ + u_n-2; ...; u_k + u_n-k+1 theo u₁, n và d.

b) Chứng tỏ rằng 2(u₁ + u₂ + u₃ + ... + u_n) = n(u₁ + u_n).

Lời giải:

a) Ta có: u_n = u₁ + (n – 1)d, u_n-1 = u₁ + (n – 1 – 1)d = u₁ + (n – 2)d

Khi đó:

u₁ + u_n = u₁ + u₁ + (n – 1)d = 2u₁ + (n – 1)d;

u₂ + u_n-1 = u₁ + d + u₁ + (n – 2)d = 2u₁ + (n – 1)d;

u₃ + u_n-2 = u₁ + 2d + u₁ + (n – 3)d = 2u₁ + (n – 1)d;

...

u_k + u_n-k+1 = u₁ + (k – 1)d + u₁ + (n – k + 1 – 1)d = 2u₁ + (n – 1)d;

Vậy u₁ + u_n = u₂ + u_n-1 = u₃ + u_n-2 = ... = u_k + u_n-k+1.

b) Ta có: 2(u₁ + u₂ + u₃ + ... + u_n)

= 2[(u₁ + u_n) + (u₂ + u_n-1) + (u₃ + u_n-2) + ... + (u_k + u_n-k+1)]

= 2[(u₁ + u_n) + (u₁ + u_n) + ... + (u₁ + u_n)]

= $2.\frac{n}{2}\left(u_1+u_n\right)$ = n(u₁ + u_n) .

Thực hành 4 trang 55 Toán 11 Tập 1:

a) Tính tổng 50 số tự nhiên chẵn đầu tiên.

b) Cho cấp số cộng (u_n) có u₃ + u₂₈ = 100. Tính tổng 30 số hạng đầu tiên của cấp số cộng đó.

c) Cho cấp số cộng (v_n) có S₆ = 110. Tính S₂₀.

Lời giải:

a) 50 số tự nhiên chẵn lập thành một cấp số cộng, có u₁ = 0, công sai d = 2.

Khi đó tổng của 50 số này là:

$S_{50}=\frac{50(0+50)}{2}=1250$.

b) Ta có: u₃ + u₂₈ = u₁ + 2d + u₁ + 27d = 2u₁ + 29d = 100

Tổng của 30 số hạng đầu tiên của cấp số cộng đó là:

$S_{30}=\frac{30\left(u_1+u_{30}\right)}{2}=\frac{30.\left(u_1+u_1+29d\right)}{2}=\frac{30\left(2u_1+29d\right)}{2}=\frac{30.100}{2}=1500$.

c) Ta có: $S_6=\frac{6\left(u_1+u_6\right)}{2}=\frac{6.\left(u_1+u_1+5d\right)}{2}=\frac{6\left(2u_1+5d\right)}{2}=18\iff 2u_1+5d=6$

Tổng của 10 số hạng đầu tiên của cấp số cộng đó là:

$S_{10}=\frac{10\left(u_1+u_{10}\right)}{2}=\frac{10.\left(u_1+u_1+9d\right)}{2}=\frac{10\left(2u_1+9d\right)}{2}=110\iff 2u_1+9d=22$.

Khi đó ta có hệ phương trình: .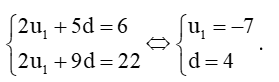

Tổng 20 số hạng đầu tiên của cấp số cộng là:

$S_{10}=\frac{10\left(u_1+u_{10}\right)}{2}=\frac{10.\left(u_1+u_1+9d\right)}{2}=\frac{10\left(2u_1+9d\right)}{2}=110\iff 2u_1+9d=22$.

Vận dụng 3 trang 55 Toán 11 Tập 1: Một rạp hát có 20 hàng ghế xếp theo hình quạt. Hàng thứ nhất có 17 ghế, hàng thứ hai có 20 ghế, hàng thứ ba có 23 ghế, ... cứ thế tiếp tục cho đến hàng cuối cùng (Hình 4).

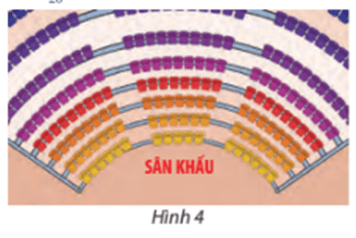
Lời giải:

Số ghế của mỗi hàng lập thành một cấp số cộng, có số hạng đầu là u₁ = 7, công sai d = 3. Khi đó số hạng tổng quát của cấp số cộng là: u_n = u₁ + (n – 1)d = 7 + (n – 1).3.

a) Số ghế có ở hàng cuối cùng (hàng số 20) là: u₂₀ = 17 + (20 – 1).3 = 74.

b) Tổng số ghế có trong rạp là tổng của 20 số hạng đầu trong cấp số cộng và bằng:

$S_{20}=\frac{20\left(17+74\right)}{2}=910$.

Vậy tổng số ghế trong rạp là 910 ghế.

Bài tập

Bài 1 trang 56 Toán 11 Tập 1: Chứng minh dãy số hữu hạn sau là cấp số cộng: 1; – 3; – 7; – 11; – 15.

Lời giải:

Dãy số 1; – 3; – 7; – 11; – 15 có số hạng đầu là u₁ = 1, từ số hạng thứ hai trở đi ta thấy số hạng sau hơn số hạng trước – 4 đơn vị nên đây là một cấp số cộng có công sai d = – 4.

Bài 2 trang 56 Toán 11 Tập 1: Cho (u_n­) là cấp số cộng với số hạng đầu u₁ = 4 và công sai d = – 10. Viết công thức số hạng tổng quát u_n.

Lời giải:

Công thức số hạng tổng quát của dãy số (u_n) có số hạng đầu u₁ = 4 và công sai d = – 10 là:

u_n = 4 + (n – 1).10 = 10n – 6.

Bài 3 trang 56 Toán 11 Tập 1: Cho cấp số cộng (u_n­) có số hạng đầu u₁ = – 3 và công sai d = 2.

a) Tìm u₁₂;

b) Số 195 là số hạng thứ bao nhiêu của cấp số cộng đó?

Lời giải:

Số hạng tổng quát của cấp số cộng (u_n) với số hạng đầu u₁ = – 3 và công sai d = 2 là:

u_n = – 3 + (n – 1).2 = 2n – 5.

a) Ta có u₁₂ = 2.12 – 5 = 19.

b) Xét u_n = 195

⇔ 2n – 5 = 195

⇔ n = 100

Vậy số 195 là số hạng thứ 100 của cấp số cộng.

Bài 4 trang 56 Toán 11 Tập 1: Trong các dãy số sau đây, dãy số nào là cấp số cộng? Tìm số hạng đầu và công sai của nó.

a) u_n = 3 – 4n;

b) u_n = $\frac{n}{2}-4$;

c) u_n = 5ⁿ;

d) u_n = $\frac{9-5n}{3}$.

Lời giải:

a) Ta có:

u₁ = 3 – 4.1 = – 1;

u_n+1 = 3 – 4(n + 1) = 3 – 4n – 4 = u_n – 4, ∀n ∈ ℕ^*.

Vậy (u_n) là một cấp số cộng có số hạng đầu là – 1 và công sai d = – 4.

b) Ta có:

u₁ = $\frac{1}{2}-4=\frac{-7}{2}$;

u_n+1 = $\frac{n+1}{2}-4=\frac{n}{2}-4+\frac{1}{2}=u_n+\frac{1}{2},\forall n\in {\mathbb{N}}^{*}$.

Vậy (u_n) là một cấp số cộng có số hạng đầu là $-\frac{7}{2}$ và công sai $d=\frac{1}{2}$.

c) Dãy số (u_n) không phải cấp số cộng vì:

u₁ = 5¹ = 5; u₂ = 5² = 25; u₂ = 5³ = 125 và $u_2\ne \frac{1}{2}\left(u_1+u_3\right)$.

d) Ta có:

u₁ = $\frac{9-5.1}{3}=\frac{4}{3}$

u_n+1 = $\frac{9-5\left(n+1\right)}{3}=\frac{9-5n-5}{3}=\frac{9-5n}{3}-\frac{5}{3}=u_n-\frac{5}{3},\forall n\in {\mathbb{N}}^{*}$.

Vậy (u_n) là một cấp số cộng có số hạng đầu là $\frac{4}{3}$ và công sai $d=-\frac{5}{3}$.

Bài 5 trang 56 Toán 11 Tập 1: Tìm số hạng đầu và công sai của cấp số cộng (u_n), biết:

a) ;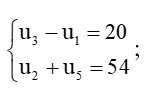

b) ;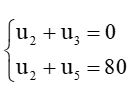

c) .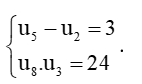

Lời giải:

a) .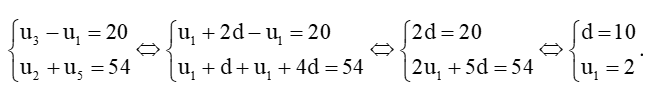

Vậy cấp số cộng (u_n) có số hạng đầu u₁ = 2 và công sai d = 10.

b) 

Vậy cấp số cộng (u_n) có số hạng đầu u₁ = – 60 và công sai d = 40.

c) 

$\iff$.

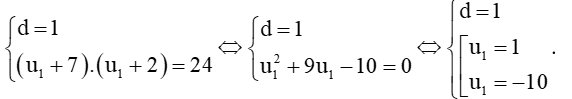
Vậy cấp số cộng (u_n) có số hạng đầu u₁ = 1 và công sai d = 1 hoặc số hạng đầu u₁ = – 10 và công sai d = 1.

Bài 6 trang 56 Toán 11 Tập 1: Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm, 41 cm, ..., 31 cm.

a) Cái thang đó có bao nhiêu bậc?

b) Tính chiều dài thanh gỗ mà người đó cần mua, giả sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể.

Lời giải:

a) Dãy số 45; 43; 41; ...; 31 là một cấp số cộng có số hạng đầu u₁ = 45 và công sai d = 2. Khi đó số hạng tổng quát của cấp số cộng trên là:

u_n = 45 + (n – 1)(– 2) = 47 – 2n, ∀n ∈ ℕ^*.

Thanh cuối cùng có độ dài là 31 cm nên để tìm thang có bao nhiêu bậc tương ứng với tìm thanh ngang cuối cùng là số hạng thứ bao nhiêu trong cấp số cộng trên.

Ta có u_n = 47 – 2n = 31

⇔ n = 8

Vậy cái thang có 8 bậc.

b) Chiều dài thanh gỗ cần mua là tổng của 8 số hạng đầu tiên của cấp số cộng và bằng $S_8=\frac{8\left(45+31\right)}{2}=304\left(cm\right)$.

Bài 7 trang 56 Toán 11 Tập 1: Khi một vận động viên nhảy dù nhảy xa khỏi máy bay, giả sử quãng đường người ấy rơi tự do (tính theo feet) trong mỗi giây liên tiếp theo thứ tự trước khi bung dủ lần lượt là: 16; 48; 80; 112; 144; ... (các quãng đường này tạo thành cấp số cộng).

a) Tính công sai của cấp số cộng trên.

b) Tính tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên.

Lời giải:

a) Các quãng đường tạo thành cấp số cộng có công sai d = 48 – 16 = 32.

b) Cấp số cộng có số hạng đầu tiên là u₁ = 16 và công sai d = 32, khi đó công thức số hạng tổng quát là: u_n = 16 + (n – 1).32 = 32n – 16.

Sau 10 giây buông dù quãng đường người đó rơi tự do là:

u₁₀ = 32.10 – 16 = 304 (feet).

Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên cũng chính là tổng của 10 số hạng đầu tiên trong cấp số cộng và bằng:

$S_{10}=\frac{10\left(16+304\right)}{2}=1600$.

Vậy tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1 600 feet.

Bài 8 trang 56 Toán 11 Tập 1: Ở một loài thực vật lưỡng bội, tính trạng chiều cao cây do hai gene không alen là A và B cùng quy định kiểu tương tác cộng gộp. Trong kiểu gene nếu cứ thêm một alen trội A hay B thì chiều cao cây tăng thêm 5 cm. Khi trưởng thành, cây thấp nhất của loài này với kiểu gene aabb có chiều cao 100cm. Hỏi cây cao nhất với kiểu gene AABB có chiều cao bao nhiêu?

Lời giải:

Chiều cao của các cây lập thành một cấp số cộng u_n

Cây thấp nhất có kiểu gene aabb nên u₁ = 100.

Nếu cứ thêm một alen trội A hay B thì chiều cao cây tăng thêm 5 cm do đó công sai của cấp số cộng là d = 5.

Vậy cây cao nhất với kiểu gene AABB có chiều cao là 100 + 5.4 = 120 (cm).

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số