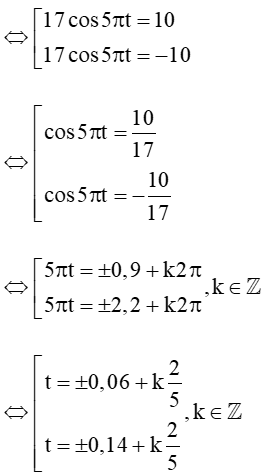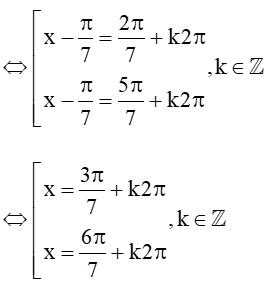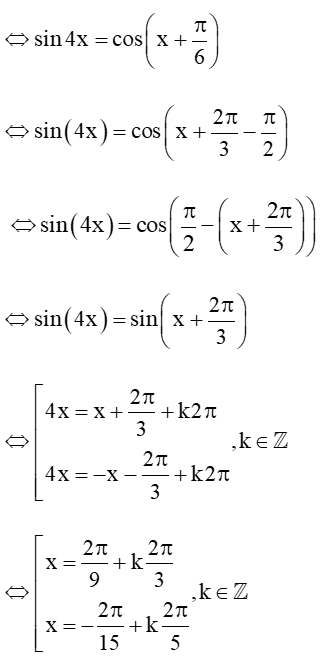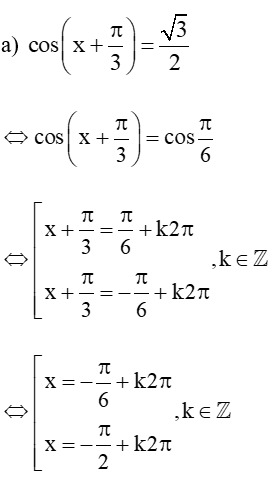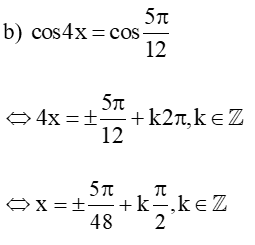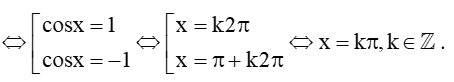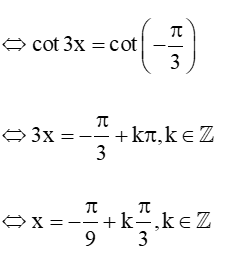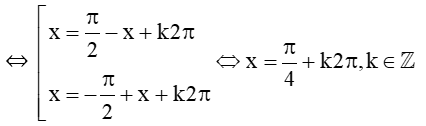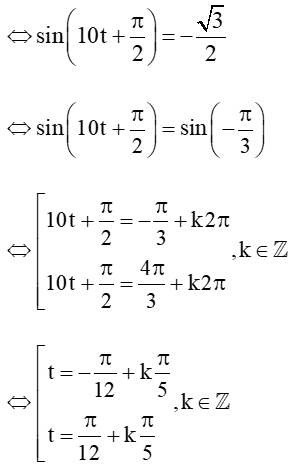Giải SGK Toán 11 (Chân trời sáng tạo) Bài 5: Phương trình lượng giác

Giải Toán 11 Bài 5: Phương trình lượng giác

Hoạt động khởi động trang 34 Toán 11 Tập 1: Trong hình bên, khi bàn đạp xe đạp quay, bóng M của đầu trục quay dao động trên mặt đất quanh điểm O theo phương trình s = 17cos5πt với s (cm) là tọa độ của điểm M trên trục Ox và t (giây) là thời gian bàn đạp quay. Làm cách nào để xác định được các thời điểm mà tại đó độ dài bóng OM bằng 10cm?

Lời giải:

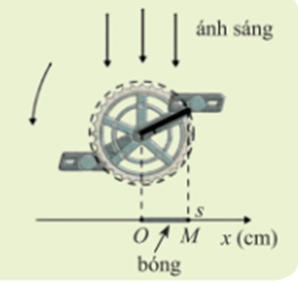
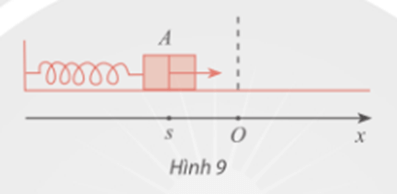
Để xác định được các thời điểm mà tại đó độ dài bóng OM bằng 10cm thì s = 10

⇔ 17cos5πt = 10

Ta cần giải phương trình cos5πt = $\frac{10}{17}$

Bài học này sẽ giúp chúng ta giải quyết phương trình trên.

1. Phương trình tương đương

Hoạt động khám phá 1 trang 34 Toán 11 Tập 1: Xác định và so sánh tập nghiệm của các phương trình sau:

a) x – 1 = 0;

b) x² – 1 = 0;

c) $\sqrt{2x^2-1}=x$.

Lời giải:

a) x – 1 = 0 ⇔ x = 1.

Vậy tập nghiệm của phương trình là S₁ = {1}.

b) x² – 1 = 0 ⇔ x = 1 hoặc x = – 1

Vậy tập nghiệm của phương trình là S₂ = { – 1; 1}.

c) $\sqrt{2x^2-1}=x$

$\Rightarrow 2x^2-1=x^2$

$\Rightarrow x^2=1$

Thay x = 1 và x = – 1 vào phương trình ban đầu ta thấy x = 1 là thỏa mãn.

Vậy tập nghiệm của phương trình là S₃ = {1}.

Ta có nhận xét:

S₁ = S₃ ⊂ S₂.

Thực hành 1 trang 35 Toán 11 Tập 1: Chỉ ra lỗi sai trong phép biến đổi phương trình dưới đây:

$x^2=2x\iff \frac{x^2}{x}=2\iff x=2$

Lời giải:

Lỗi sai: Phương trình x² = 2x và phương trình $\frac{x^2}{x}=2$ không tương đương vì:

Phương trình x² = 2x có tập nghiệm S₁ = {0; 2}.

Phương trình $\frac{x^2}{x}=2$ có tập nghiệm S₂ = {2}.

2. Phương trình sinx = m

Hoạt động khám phá 2 trang 35 Toán 11 Tập 1: a) Có giá trị nào của x để sinx = 1,5 không?

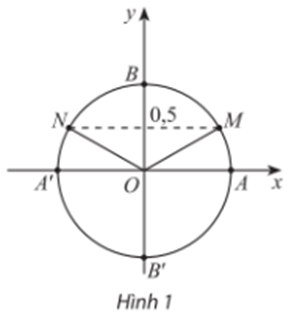
b) Trong Hình 1, những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có sinx = 0,5? Xác định số đo của các góc lượng giác đó.

Lời giải:

a) Vì – 1 ≤ x ≤ 1 mà 1,5 > 1 nên không tồn tại giá trị của x để sinx = 1,5.

b) Trên Hình 1, những điểm trên đường tròn biểu diễn góc lượng giác x có sinx = 0,5 là điểm M và N.

Điểm M biểu diễn cho các góc lượng giác có số đo là $\frac{\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

Điểm N biểu diễn cho các góc lượng giác có số đo là $\frac{5\pi }{6}+k2\pi ,k\in \mathbb{Z}$.

Thực hành 2 trang 36 Toán 11 Tập 1: Giải các phương trình sau:

a) sinx = $\frac{\sqrt{3}}{2}$;

b) sin(x + 30°) = sin(x + 60°).

Lời giải:

a) sinx = $\frac{\sqrt{3}}{2}$

Vì sin$\frac{\pi }{3}$ = $\frac{\sqrt{3}}{2}$ nên phương trình sinx = $\frac{\sqrt{3}}{2}$= sin$\frac{\pi }{3}$ có các nghiệm là:

$\text{x}=\frac{\pi }{3}+k2\pi$ và $x=\frac{2\pi }{3}+k2\pi$, k ∈ ℤ.

Vậy tập nghiệm của phương trình đã cho là: S = $\left(\frac{\pi }{3}+k2\pi ,\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}\right)$.

b) sin(x + 30°) = sin(x + 60°)

⇔ x + 30° = x + 60° + k360° hoặc x + 30° = 360° – x – 60° + k360° (k ∈ ℤ)

⇔ 30° = 60° + k360° (vô lí) hoặc x = 150° + k180° (k ∈ ℤ).

Vậy tập nghiệm của phương trình đã cho là: S = {150° + k180°, k ∈ ℤ}.

3. Phương trình cosx = m

Hoạt động khám phá 3 trang 36 Toán 11 Tập 1: Trong Hình 3, những điểm nào trên đường tròn lượng giác biểu diễn diễn góc lượng giác x có cosx = $-\frac{1}{2}$? Xác định số đo của các góc lượng giác đó.

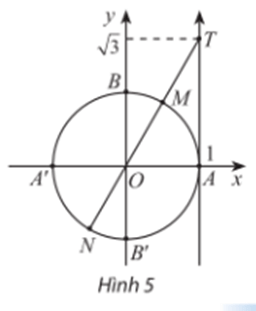
Lời giải:

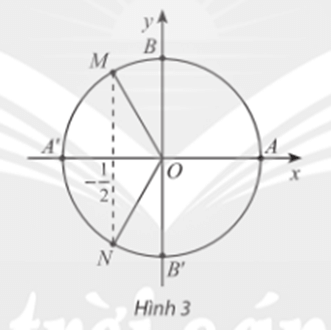
Trên đường tròn lượng giác điểm M và N biểu diễn diễn góc lượng giác x có cosx = $-\frac{1}{2}$.

Điểm M là điểm biểu diễn cho các góc lượng giác có số đo là: $\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Điểm N là điểm biểu diễn cho các góc lượng giác có số đo là: $-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Thực hành 3 trang 37 Toán 11 Tập 1: Giải các phương trình sau:

a) cosx = – 3;

b) cosx = cos15°;

c) $\text{cos}\left(x+\frac{\pi }{12}\right)=\text{cos}\frac{3\pi }{12}$.

Lời giải:

a) Vì – 3 < – 1 nên phương trình cosx = – 3 vô nghiệm.

b) cosx = cos15°

⇔ x = 15° + k360° hoặc x = – 15° + k360° .

Vậy tập nghiệm của phương trình là S = {15° + k360°; – 15° + k360°, k ∈ ℤ}.

c) $\text{cos}\left(x+\frac{\pi }{12}\right)=\text{cos}\frac{3\pi }{12}$

$\iff x+\frac{\pi }{12}=\frac{3\pi }{12}+k2\pi$ hoặc $x+\frac{\pi }{12}=-\frac{3\pi }{12}+k2\pi ,k\in \mathbb{Z}$

$\iff x=\frac{\pi }{6}+k2\pi$ hoặc $x=-\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$

Vậy tập nghiệm của phương trình là S = $\left(\frac{\pi }{6}+k2\pi ;-\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}\right)$.

4. Phương trình tanx = m

Hoạt động khám phá 4 trang 37 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho T là điểm trên trục tang có tọa độ là (1; $\sqrt{3}$) (Hình 5). Những điểm nào trên đường tròn lượng giác biểu diễn góc lượng giác x có tanx = $\sqrt{3}$? Xác định số đo của các góc lượng giác đó.

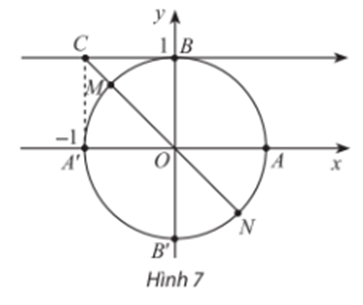
Lời giải:

Ta thấy M và N là hai điểm biểu diễn các góc lượng giác thỏa mãn tanx = $\sqrt{3}$.

Điểm M là điểm biểu diễn các góc lượng giác có số đo $\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Điểm N là điểm biểu diễn các góc lượng giác có số đo $-\frac{2\pi }{3}+k\pi ,k\in \mathbb{Z}$.

Thực hành 4 trang 38 Toán 11 Tập 1: Giải các phương trình sau:

a) tanx = 0;

b) tan(30° – 3x) = tan75°.

Lời giải:

a) Điều kiện xác định là: $x\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

Vì tan0 = 0 nên phương trình tanx = 0 có các nghiệm x = kπ, k ∈ ℤ.

Vậy tập nghiệm của phương trình là: S = {kπ, k ∈ ℤ}.

b) tan(30° – 3x) = tan75°

⇔ tan(3x – 30°) = tan(– 75°)

⇔ 3x – 30° = – 75° + k360°, k ∈ ℤ

⇔ 3x = – 45° + k360°, k ∈ ℤ

⇔ x = – 15° + k120°, k ∈ ℤ

Vậy tập nghiệm của phương trình là: S = { – 15° + k120°, k ∈ ℤ}.

5. Phương trình cotx = m

Hoạt động khám phá 5 trang 38 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho C là điểm trên trục côtang có tọa độ là (– 1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có cotx = – 1? Xác định số đo của các góc lượng giác đó.

Lời giải:

Trên đường tròn lượng giác hai điểm M và N biểu diễn các góc lượng giác có số đo góc x thỏa mãn cotx = – 1.

Điểm M biểu diễn các góc lượng giác có số đo góc $\frac{3\pi }{4}+k2\pi ,k\in \mathbb{Z}$.

Điểm N biểu diễn các góc lượng giác có số đo góc $-\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$.

Thực hành 5 trang 39 Toán 11 Tập 1: Giải các phương trình sau:

a) cotx = 1;

b) cot(3x + 30°) = cot75°.

Lời giải:

a) Vì cot$\frac{\pi }{4}$= 1 nên phương trình cotx = 1 có các nghiệm là $x=\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$.

Vậy tập nghiệm của phương trình là: S = $\left(\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}\right)$.

b) cot(3x + 30°) = cot75°

⇔ 3x + 30° = 75° + k180°, k ∈ ℤ

⇔ 3x = 45° + k180°, k ∈ ℤ

⇔ x = 15° + k60°, k ∈ ℤ

Vậy tập nghiệm của phương trình là: S = {15° + k60°, k ∈ ℤ}.

Thực hành 6 trang 40 Toán 11 Tập 1: Sử dụng máy tính cầm tay để giải các phương trình sau:

a) cosx = 0,4;

b) tanx = $\sqrt{3}$.

Lời giải:

a) Sử dụng máy tính cầm tay ta có: cos1,16 ≈ 0,4 nên cosx = cos1,16 do đó các nghiệm của phương trình là x = 1,16 + k2π và x = – 1,16 + k2π với k ∈ ℤ.

Vậy tập nghiệm của phương trình là S = {1,16 + k2π; – 1,16 + k2π, k ∈ ℤ}.

b) Sử dụng máy tính cầm tay ta có: tan$\frac{\pi }{3}$ = $\sqrt{3}$ nên tanx = tan$\frac{\pi }{3}$ do đó các nghiệm của phương trình là x = $\frac{\pi }{3}$ + k$\pi$ với k ∈ ℤ.

Vậy tập nghiệm của phương trình là S = $\left(\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}\right)$.

Vận dụng trang 40 Toán 11 Tập 1: Quay lại bài toán khởi động, phương trình chuyển động của bóng đầu trục bàn đạp là x = 17cos5πt (cm) với t được đo bằng giây. Xác định các thời điểm t mà tại đó độ dài bóng |x| bằng 10 cm. Làm tròn kết quả đến hàng phần mười.

Lời giải:

Xét phương trình |17cos5πt| = 10

Độ dài bóng |x| bằng 10 cm tại các thời điểm t = $\pm$0,06 +k$\frac{2}{5}$, t = $\pm$0,14 + k$\frac{2}{5}$ (k$\in$Z).

Bài tập

Bài 1 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) sin2x = $\frac{1}{2}$;

b) sin$\left(x-\frac{\pi }{7}\right)$ = sin$\frac{2\pi }{7}$;

c) sin4x - cos$\left(x+\frac{\pi }{6}\right)$ = 0.

Lời giải:

a) Vì sin$\frac{\pi }{6}$ = $\frac{1}{2}$ nên ta có phương trình sin2x = sin$\frac{\pi }{6}$

Vậy tập nghiệm của phương trình là: S = $\left(\frac{\pi }{12}+k\pi ,\frac{5\pi }{12}+k\pi ,k\in \mathbb{Z}\right)$.

b) sin$\left(x-\frac{\pi }{7}\right)$= sin$\frac{2\pi }{7}$

Vậy tập nghiệm của phương trình là: S = $\left(\frac{3\pi }{7}+k2\pi ;\frac{6\pi }{7}+k2\pi ,k\in \mathbb{Z}\right)$.

c) sin4x - cos$\left(x+\frac{\pi }{6}\right)$ = 0

Vậy tập nghiệm của phương trình là: S = $\left(\frac{2\pi }{9}+k\frac{2\pi }{3};-\frac{2\pi }{15}+k\frac{2\pi }{5},k\in \mathbb{Z}\right)$.

Bài 2 trang 40 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cos$\left(x+\frac{\pi }{3}\right)=\frac{\sqrt{3}}{2}$;

b) cos4x = cos$\frac{5\pi }{12}$;

c) cos²x = 1.

Lời giải:

Vậy tập nghiệm của phương trình là: S = $\left(-\frac{\pi }{6}+k2\pi ;-\frac{\pi }{2}+k2\pi ,k\in \mathbb{Z}\right)$.

Vậy tập nghiệm của phương trình là: S = $\left(\pm \frac{5\pi }{48}+k\frac{\pi }{2},k\in \mathbb{Z}\right)$.

c) cos²x = 1

Vậy tập nghiệm của phương trình là: S = {k$\pi$, k$\in$Z}.

Bài 3 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) tanx = tan55°;

b) tan$\left(2x+\frac{\pi }{4}\right)$=0.

Lời giải:

a) tanx = tan55° (điều kiện xác định x ≠ 90° + k180°).

⇔ x = 55° + k180°, k ∈ ℤ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình S = {55° + k180°, k ∈ ℤ}.

b) tan$\left(2x+\frac{\pi }{4}\right)$=0 (điều kiện xác định $2x+\frac{\pi }{4}\ne \frac{\pi }{2}+k2\pi \iff x\ne \frac{\pi }{8}+k\pi ,k\in \mathbb{Z}$)

$\iff 2x+\frac{\pi }{4}=k\pi ,k\in \mathbb{Z}$

$\iff x=-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}$ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình là S = $\left(-\frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}\right)$.

Bài 4 trang 41 Toán 11 Tập 1: Giải các phương trình lượng giác sau:

a) cot$\left(\frac{1}{2}x+\frac{\pi }{4}\right)$= -1;

b) cot3x = $-\frac{\sqrt{3}}{3}$.

Lời giải:

a) cot$\left(\frac{1}{2}x+\frac{\pi }{4}\right)$ = -1 (điểu kiện xác định x # $\frac{\pi }{2}$ + k2$\pi$, k$\in$Z)

$\iff \frac{1}{2}x+\frac{\pi }{4}=-\frac{\pi }{4}+k\pi ,k\in \mathbb{Z}$

$\iff x=-\pi +k2\pi ,k\in \mathbb{Z}$ (thỏa mãn điều kiện)

Vậy tập nghiệm của phương trình là S = $\left(-\pi +k2\pi ,k\in \mathbb{Z}\right)$.

b) cot3x = $-\frac{\sqrt{3}}{3}$ (điểu kiện xác định x # k$\frac{\pi }{3}$, k$\in$Z)

Vậy tập nghiệm của phương trình là S = $\left(-\frac{\pi }{9}+k\frac{\pi }{3},k\in \mathbb{Z}\right)$.

Bài 5 trang 41 Toán 11 Tập 1: Tại các giá trị nào của x thì đồ thị hàm số y = cosx và y = sinx giao nhau?

Lời giải:

Xét phương trình hoành độ giao điểm: sinx = cosx

⇔ cosx = cos$\left(\frac{\pi }{2}-x\right)$

Vậy tập nghiệm của bất phương trình là: S = $\left(\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}\right)$.

Bài 6 trang 41 Toán 11 Tập 1: Trong Hình 9, khi được kéo ra khỏi vị trí cân bằng ở điểm O và buông tay, lực đàn hồi của lò xo khiến vật A gắn ở đầu của lò xo dao động quanh O. Tọa độ s (cm) của A trên trục Ox vào thời điểm t (giây) sau khi buông tay được xác định bởi công thức s = 10sin$\left(10t+\frac{\pi }{2}\right)$. Vào các thời điểm nào thì s = -5$\sqrt{3}$ cm?

(Theo https://www.britannica.com/science/simple-harmonic-motion )

Lời giải:

Xét phương trình: 10sin$\left(10t+\frac{\pi }{2}\right)$ = -5$\sqrt{3}$

Vậy vào các thời điểm $t=-\frac{\pi }{12}+k\frac{\pi }{5}\left(k\ge 1,k\in \mathbb{Z}\right)$ và $t=\frac{\pi }{12}+k\frac{\pi }{5}\left(k\ge 0,k\in \mathbb{Z}\right)$ thì s = -5$\sqrt{3}$ cm.

Bài 7 trang 41 Toán 11 Tập 1: Trong Hình 10, ngọn đèn hải đăng H cách bờ biển yy’ một khoảng HO = 1km. Đèn xoay ngược chiều kim đồng hồ với tốc độ $\frac{\pi }{10}$ rad/s và chiếu hai luồng ánh sáng về hai phía đối diện nhau. Khi đèn xoay, điểm M mà luồng ánh sáng của hải đăng rọi vào bờ biển chuyển động dọc theo bờ.

(Theo https://www.mnhs.org/splitrock/learn/technology)

a) Ban đầu luồng sáng trùng với đường thẳng HO. Viết hàm số biểu thị tọa độ y_M của điểm M trên trục Oy theo thời gian t.

b) Ngôi nhà N nằm trên bờ biển với tọa độ y_S = – 1 (km). Xác định các thời điểm t mà đèn hải đăng chiếu vào ngôi nhà.

Lời giải:

a) Sau t giây điểm M quét được một góc lượng giác có số đo là: $\alpha =\frac{\pi }{10}t$ rad.

Xét tam giác HOM vuông tại O có:

MO = tanα.1 = tan$\left(\frac{\pi }{10}t\right)$.

Vậy tọa độ y_M = tan$\left(\frac{\pi }{10}t\right)$.

b) Xét tan$\left(\frac{\pi }{10}t\right)$ = -1

$\iff$ tan$\left(\frac{\pi }{10}t\right)$ = tan$\left(-\frac{\pi }{4}\right)$

$\iff$ $\frac{\pi }{10}t$ = $-\frac{\pi }{4}$ + k$\pi$, k$\in$Z

$\iff$ t = -2,5 + 10k, k$\in$Z

Vì t ≥ 0 nên tại các thời điểm t = -2,5 + 10k, k$\in$Z, k$\ge$1 thì đèn hải đăng chiếu vào ngôi nhà.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị giác

Bài tập cuối chương 1

Bài 1: Dãy số

Bài 2: Cấp số cộng