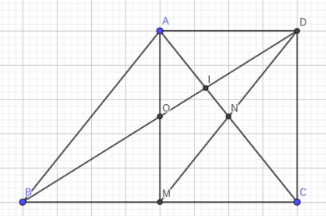
Cho Δ A B C cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N

Đề bài: Cho $\Delta ABC$ cân tại A, AM là đường cao. Gọi N là trung điểm của AC. D là điểm đối xứng của M qua N.

a) CMR : tứ giác ADCM là hình chữ nhật$DI =\frac{2}{3} OB$

b) CMR : tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM

c) BD cắt AC tại I. CMR : $DI=\frac{2}{3}OB$

Trả lời

Hướng dẫn giải:

a.Ta có: N là trung điểm AC
M,D đối xứng qua N→ N là trung điểm MD

$\Rightarrow AC\cap DM=N$ là trung điểm mỗi đường
Vì $\text{AM}\perp \text{BC}$

$\Rightarrow AM\perp MC\Rightarrow AMCD$ là hình chữ nhật
 b.Vì $\text{ΔABC}$ cân tại $A,AM\perp BC\Rightarrow M$ là trung điểm $BC\Rightarrow MB=MC$

 AMCD là hình chữ nhật ⇒ AD // CM, AD = CM
⇒ AD // BM, AD = BM

⇒ ABMD là hình bình hành

$\Rightarrow AM\cap BD$ tại trung điểm mỗi đường
Gọi $AM\cap BD=O$

⇒ O là trung điểm AM, BD
⇒ BD đi qua trung điểm O của AM
c) Vì O, N là trung điểm AM,DM và $AN\cap DO=I$

⇒ I là trọng tâm $\text{ΔMAD}$

$\Rightarrow DI=\frac{2}{3}DO$

Vì O là trung điểm BD → OB = OD

$\Rightarrow DI=\frac{2}{3}OB$