Cho hình bình hành ABCD có góc A = 120 độ. Tia phân giác của góc D qua trung điểm I của AB

Đề bài. Cho hình bình hành ABCD có $\widehat{A}={120}^{\circ }$. Tia phân giác của $\widehat{D}$ qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:

a) AB = 2AD.

b) DI = 2AH.

c) AC vuông góc với AD.

Trả lời

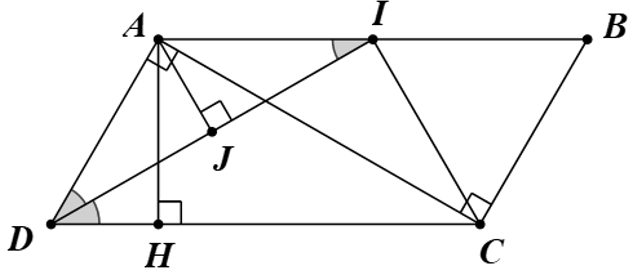a) Hình bình hành ABCD có $\widehat{BAD},\widehat{ADC}$ ở vị trí trong cùng phía.

Suy ra $\widehat{ADC}={180}^{\circ }\mathrm{ }-\widehat{BAD}={60}^{\circ }$

Khi đó $\widehat{ADI}=\widehat{IDC}=\frac{\widehat{ADC}}{2}={30}^{\circ }$ (do DI là tia phân giác của $\widehat{ADC}$).

Mà $\widehat{AID}=\widehat{IDC}$(cặp góc so le trong).

Vì vậy $\widehat{AID}=\widehat{ADI}$

Suy ra tam giác ADI cân tại A.

Do đó AD = AI.

Mà AB = 2AI (I là trung điểm của AB).

Vậy AB = 2AD (điều phải chứng minh).

b) Gọi J là trung điểm của DI.

Tam giác ADI có AJ là đường trung tuyến.

Suy ra AJ vừa là đường phân giác, vừa là đường cao của tam giác ADI.

Khi đó $\widehat{JAI}=\widehat{DAJ}=\frac{\widehat{DAI}}{2}={60}^{\circ }$

Xét ∆AJD và ∆DHA, có:

$\widehat{AJD}=\widehat{DHA}={90}^{\circ }$

AD là cạnh chung;

$\widehat{DAJ}=\widehat{ADH}={60}^{\circ }$

Do đó ∆AJD = ∆DHA (cạnh huyền – góc nhọn).

Suy ra DJ = AH (cặp cạnh tương ứng).

Mà DI = 2DJ (J là trung điểm của DI).

Vậy DI = 2AH (điều phải chứng minh).

c) Ta có BI = BC $(\frac{1}{2}AB)$

Suy ra tam giác IBC cân tại B.

Mà $\widehat{IBC}=\widehat{ADC}={60}^{\circ }$

Do đó tam giác IBC đều.

Vì vậy IC = IB = IA.

Khi đó tam giác ABC vuông tại C hay $\widehat{ACB}={90}^{\circ }$

Suy ra $\widehat{DAC}=\widehat{ACB}={90}^{\circ }$

Vậy AD ⊥ AC (điều phải chứng minh).