Cho tam giác ABC vuông tại A, đường cao AH. Biết 3.AB = 2.AC. Tính sin góc ACB, tan góc ACB

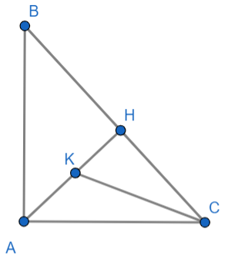
Đề bài. Cho tam giác ABC vuông tại A, đường cao AH.

a) Biết 3AB = 2AC. Tính $sin\widehat{ACB},tan\widehat{ACB}$.

b) Vẽ đường phân giác CK của tam giác AHC. Biết AH = 2,4 cm; BH = 1,8 cm. Tính CH, AC, CK, $cos\widehat{HCK}$.

Trả lời

a) $sin\widehat{ACB}=\frac{AB}{BC}=\frac{AB}{\sqrt{A{B}^2+A{C}^2}}=\frac{AB}{\sqrt{A{B}^2+\frac{9}{4}A{B}^2}}=\frac{\sqrt{13}}{2}AB$

$tan\widehat{ACB}=\frac{AB}{AC}=\frac{AB}{\frac{3}{2}AB}=\frac{2}{3}$

b) Tam giác ABC vuông tại A, AH là đường cao

AH² = BH.CH

⇒ $CH=\frac{A{H}^2}{BH}=\frac{2,4^2}{1,8}=3,2(cm)$

$AC=\sqrt{A{H}^2+H{C}^2}\mathrm{ }=4(cm)$

Tam giác AHC có CK là đường phân giác nên$\frac{HK}{AK}=\frac{HC}{AC}=\frac{3,2}{4}\Rightarrow HK=\frac{4}{5}AK=\frac{4}{9}AH$

HK = $\frac{4}{9}.2,4=1,067cm$

$cos\widehat{HCK}=\frac{HC}{KC}=\frac{HC}{\sqrt{H{C}^2+K{H}^2}}=\frac{3,2}{\sqrt{3,2^2+1,{067}^2}}=0,948$.