Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC đến (O) (B, C là các tiếp điểm)

Đề bài. Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC đến (O) (B, C là các tiếp điểm).

a) Chứng minh: OA vuông góc với BC tại H.

b) Vẽ đường thẳng vuông góc với OB tại O cắt cạnh AC tại E. Chứng minh: ∆OAE là tam giác cân.

c) Trên tia đối của tia BC lấy điểm Q. Vẽ hai tiếp tuyến QM, QN đến (O) (M, N là tiếp tuyến). Chứng minh: 3 điểm A, M, N thẳng hàng.

Trả lời

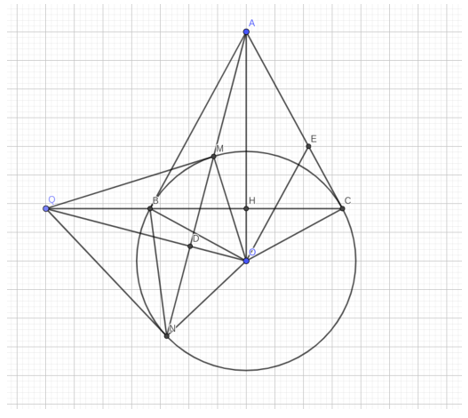a. Vì AB, AC là tiếp tuyến của (O)
⇒ AO ⊥ BC = H

b. Ta có: OE ⊥ OB

⇒ OE // AB vì AB là tiếp tuyến của (O)

⇒ OB ⊥ AB

⇒ $\widehat{CAO}=\widehat{OAB}=\widehat{AOE}$

⇒ΔOAE cân tại E

c.Ta có : AB,AC là tiếp tuyến của (O)

⇒ OB ⊥ AB mà BC⊥AB = H

⇒ OH.OA = OB² = R²

Tương tự QM, QN là tiếp tuyến của (O)

Gọi QO ∩ MN = D

⇒ OD.OQ = OM² = R² vì OM ⊥ QM

⇒ OH.OA = OD.OQ

⇒ $\frac{OH}{OD}=\frac{OQ}{OA}$

⇒ΔODA ∽ ΔOHQ(c.g.c)

$\Rightarrow \widehat{ADO}=\widehat{QHO}\Rightarrow \widehat{ADO}={90}^{\circ }$

⇒ AD ⊥ OQ

Mà MN ⊥ OQ = D
⇒ A, M, D, N thẳng hàng