Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình 25)
1.3k
08/06/2023
Câu hỏi khởi động trang 49 Toán lớp 10 Tập 1: Bác Dũng muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 32 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông (Hình 25). Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 120 cm2.
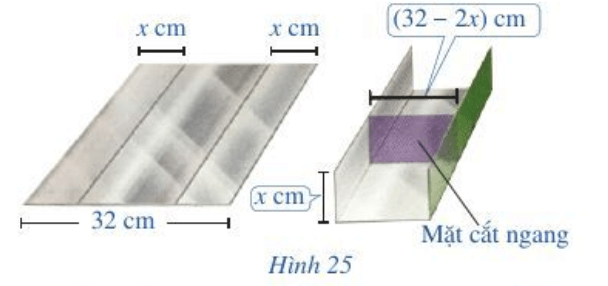
Rãnh dẫn nước phải có độ cao ít nhất là bao nhiêu xăng-ti-mét?
Trả lời
Sau khi học xong bài này ta giải được bài toán này như sau:
Tiến hành uốn tấm tôn ta được một rãnh dẫn nước có mặt cắt ngang với kích thước x (cm) và 32 – x (cm)
Khi đó diện tích mặt cắt ngang là (32 – 2x)x (cm2).
Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 120 cm2 nên ta có:
(32 – 2x)x ≥ 120 ⇔ – 2x2 + 32x – 120 ≥ 0.
Xét tam thức bậc hai – 2x2 + 32x – 120 có:
∆’ = 162 – (-2).(-120) = 16 > 0
Suy ra phương trình có hai nghiệm x1 = 6, x2 = 10.
Ta lại có hệ số a = – 2 < 0, bảng xét dấu:
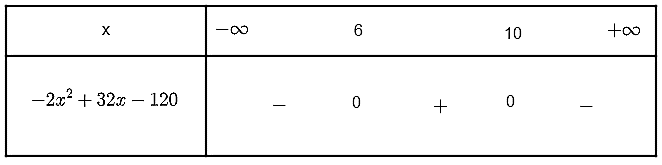
Suy ra – 2x2 + 32x – 120 ≥ 0 với mọi x ∈ [6; 10].
Vậy rãnh dẫn nước phải có độ cao ít nhất là 6 cm.
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
Bài 3: Dấu của tam thức bậc hai
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài tập cuối chương 3
Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác


