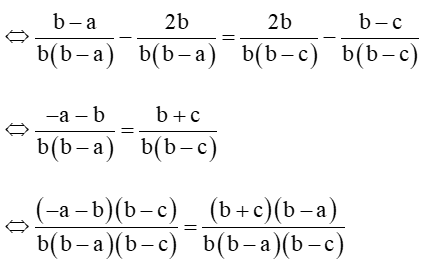Ba số 2/(b-a), 1/b, 2/(b-c) theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số a, b, c theo thứ tự lập thành cấp số nhân

Bài 4 trang 60 Toán 11 Tập 1: Ba số $\frac{2}{b-a},\frac{1}{b},\frac{2}{b-c}$ theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số a, b, c theo thứ tự lập thành cấp số nhân.

Trả lời

Ta có: $\frac{2}{b-a},\frac{1}{b},\frac{2}{b-c}$ là một cấp số cộng nên ta có:

$\frac{1}{b}-\frac{2}{b-a}=\frac{2}{b-c}-\frac{1}{b}$

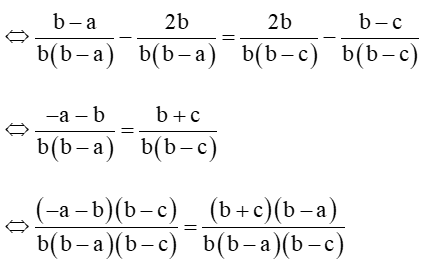
$\iff$ (-a-b)(b-c) = (b+c)(b-a)

⇔ – ab + ac – b² + bc = b² – ab + bc – ac

⇔ 2b² – 2ac = 0

⇔ b² = ac.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Dãy số

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số