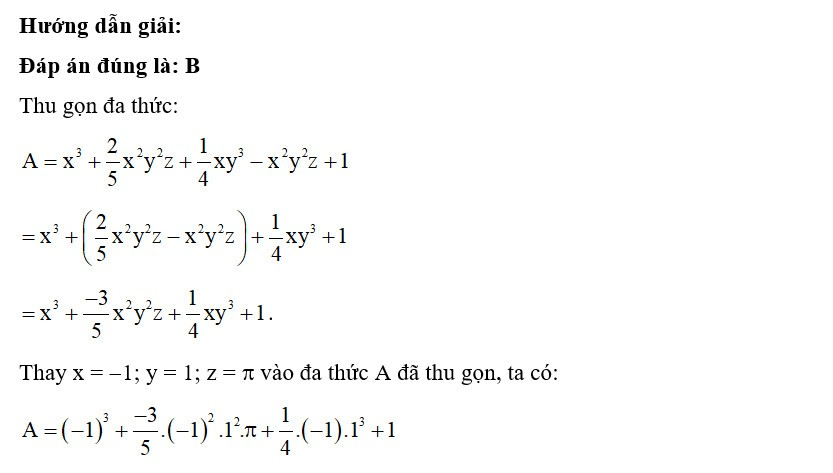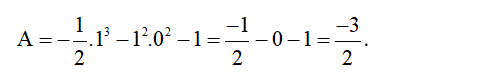10 câu hỏi trắc nghiệm thuộc Dạng 3: Tính giá trị của đa thức khi biết giá trị của biến

Trắc nghiệm Toán 8 Bài 2. Đa thức

Dạng 3: Tính giá trị của đa thức khi biết giá trị của biến

118 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Giá trị của đa thức A = -3x²y² + 2y + 2 tại x = −1; y = 1 là

A. 1;

B. 2;

C. 7;

D.9.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Thay x = 1; y = 1 vào đa thức A, ta có: A = -3.(−1)².1² + 2.1 + 2 = ‒3 + 2 + 2 = 1.

Câu 2:

Giá trị của đa thức B = 2 + 2x³y + 3x²z tại $x = \frac{1}{2}; y = 1; z = ‐ 1$ là

A. $\frac{3}{4}$ ;

B. $\frac{3}{2}$ ;

C. $\frac{9}{4}$ ;

D. $\frac{5}{2}$ .

Xem đáp án

Giá trị của đa thức B = 2 + 2x3y + 3x2z (ảnh 1)

Câu 3:

Giá trị của đa thức B = 2x.3y² + 0,5x² - 1,2y² - 5xy² + 1,5x² tại x = 0,5; y = 1 là

A. -0,2;

B. 0,45;

C. 2,3;

D. 0,25.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Thu gọn đa thức B:

B = 2x.3y² + 0,5x² - 1,2y² - 5xy² + 1,5x²

= (2.3.xy²- 5xy²) + (0,5x² + 1,5x²) - 1,2y²

= xy² + 2x² - 1,2y².

Thay x = 0,5; y = 1 vào đa thức B đã thu gọn, ta có:

B = 0,5.1² + 2.0,5² - 1,2.1² = 0,5 + 2.0,25 ‒ 1,2 = 0,5 + 0,5 ‒ 1,2 = -0,2.

Câu 4:

Giá trị gần đúng nhất của đa thức $A = x^{3} + \frac{2}{5} x^{2} y^{2} z + \frac{1}{4} x y^{3} - x^{2} y^{2} z + 1$ tại x = -1; y = 1; z = p có giá trị là

A. $\frac{3}{5} π - \frac{9}{4}$ ;

B. $\frac{‐ 3}{5} π - \frac{1}{4}$ ;

C. $\frac{‐ 3}{5} π + \frac{1}{4}$ ;

D. $\frac{3}{5} π - \frac{1}{4}$ .

Xem đáp án

Giá trị gần đúng nhất của đa thức (ảnh 1)

Câu 5:

Cho đa thức M thỏa mãn 12x²y⁴ + M = 13x²y⁴ + xy² - 1. Giá trị của đa thức M tại x = 2; y = 1 là

A. - 1;

B. 1;

C. 5;

D. -5.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Ta có: 12x²y⁴ + M = 13x²y⁴ + xy² - 1

Suy ra M = 13x²y⁴ + xy² - 1 - 12x²y⁴

= (13x²y⁴ - 12x²y⁴) + xy² - 1

= x²y⁴ + xy² - 1.

Thay x = 2; y = 1 vào M đã thu gọn, ta có:

M = 2².1⁴ + 2.1² - 1 = 4 + 2 – 1 = 5.

Câu 6:

Cho đa thức M thỏa mãn: (2xy²)².z - 2M = 2x²y⁴z + 2y⁴ - 4. Giá trị của đa thức M tại x = -1; y = 1; z = 2 là

A. 4;

B. 5;

C. 6;

D. 3.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta có: (2xy²)².z - 2M = 2x²y⁴z + 2y⁴ - 4

4x²y⁴z - 2M = 2x²y⁴z + 2y⁴ - 4

Suy ra 2M = 4x²y⁴z - (2x²y⁴z + 2y⁴ - 4)

= (4x²y⁴z - 2x²y⁴z) ‒ 2y⁴ + 4

= 2x²y⁴z ‒ 2y⁴ + 4

= 2(x²y⁴z ‒ y⁴ + 2)

Do đó M = x²y⁴z ‒ y⁴ + 2.

Thay x = -1; y = 1; z = 2 vào M đã thu gọn, ta có:

M = (-1)².1².2 ‒ 1⁴ + 2 = 2 ‒ 1 + 2 = 3.

Câu 7:

Giá trị của đa thức $A = ‐ \frac{1}{2} x^{3} - 5 y^{2} z^{2} + {(2 y z)}^{2} - 1$ tại x = 1; y = |-1|; z = |x - 1| là

A. $\frac{‐ 1}{2}$ ;

B. 1;

C. $\frac{‐ 5}{2}$ ;

D. $\frac{‐ 3}{2}$ .

Xem đáp án

Câu 8:

Cho đa thức B = (-2 + a).x + (-a).y + xy² + ax, với a là hằng số. Giá trị của B khi x = -2; y = 1 là

A. -5a + 2;

B. -5a - 6;

C. 3a - 6;

D. -3a + 3.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Thu gọn đa thức B:

B = (-2 + a).x + (-a).y + xy² + ax

= [(-2 + a).x+ ax] - ay + xy²

= (-2 + a + a).x - ay + xy²

= 2(a - 1).x - ay + xy².

Thay x = -2; y = 1 vào đa thức B đã thu gọn, ta có:

B = 2(a - 1).(-2) - a.1 + (-2).1²

= -4.(a - 1) - a - 2

= -4a + 4 - a - 2

= (-4a - a) + (4 - 2)

= -5a + 2.

Câu 9:

Cho x = 5; 2x + y² = 19, y < 0. Giá trị của đa thức A = 4x² + 3y² + 4xy - 2x² - y² - 1 là

A. 3;

B. -1;

C. 7;

D. 5.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C

Thay x = 5 vào đẳng thức 2x + y² = 19 ta có:

2.5 + y² = 19

10 + y² = 19

y² = 9.

Mà y < 0 nên y = ‒3

Thu gọn đa thức A:

A = 4x² + 3y² + 4xy - 2x² - y² - 1

= (4x² - 2x²) + (3y² - y²) + 4xy - 1

= 2x² + 2y²+ 4xy - 1

Thay x = 5; y = -3 vào đa thức A, ta có:

A = 2.5² + 2.(-3)² + 4.5.(-3) - 1

= 2.25 + 2.9 - 60 - 1

= 50 + 18 - 61

= 7.

Câu 10:

Cho x + y = 2 và đa thức:

B = x + y + 3(x + y) + 3².(x + y) + … + 3¹⁰⁰. (x + y).

Khi đó, giá trị đa thức B là

A. 2;

B. 3¹⁰¹ - 1;

C. 1;

D. 3¹⁰⁰ - 1.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

B = x + y + 3(x + y) + 3².(x + y) + … + 3¹⁰⁰. (x + y)

= (1 + 3 + 3² + … + 3¹⁰⁰).(x + y).

Đặt C = 1 + 3 + 3² + … + 3¹⁰⁰. Khi đó B = C.(x + y).

Ta có 3C = 3 + 3² + 3³ + … + 3¹⁰⁰ + 3¹⁰¹.

Trừ vế với vế của 3C cho C ta có:

2C = 3¹⁰¹ - 1.

Suy ra $C = \frac{3^{101} - 1}{2}$ .

Thay x + y = 2 và $C = \frac{3^{101} - 1}{2}$ vào đa thức B, ta có: $B = \frac{3^{101} - 1}{2} . 2 = 3^{101} - 1$ .

Bắt đầu thi ngay

Trắc nghiệm Toán 8 Bài 2. Đa thức

Dạng 3: Tính giá trị của đa thức khi biết giá trị của biến

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương