Trắc nghiệm Toán 7 KNTT Bài 14. Trường hợp bằng nhau thứ hai và thứ ba của tam giác có đáp án
Dạng 2: Chứng minh các cạnh bằng nhau và các góc bằng nhau, tính độ dài cạnh và số đo góc có đáp án
-
185 lượt thi
-
10 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Điền vào chỗ còn thiếu trong các bước chứng minh sau:
“Xét DABC và DADE có:
.............,
BC = DE.
^ABC=^ADE;
Vậy ΔABC = ∆ADE (g.c.g)”
Xem đáp án
Đáp án đúng là: B
Ta có: ΔABC = ∆ADE theo trường hợp góc – cạnh – góc nên hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh bằng nhau của hai tam giác.
Mà BC = DE và ^ABC=^ADE nên cặp góc kề tương ứng còn lại là ^ACB=^AED.
Vậy ta chọn phương án B.
Câu 2:
Cho DABC và DDEF có ˆA=ˆD,ˆB=ˆE. Để DABC = DDEF theo trường hợp góc – cạnh – góc thì phải thêm điều kiện nào sau đây:
Xem đáp án
Đáp án đúng là: A
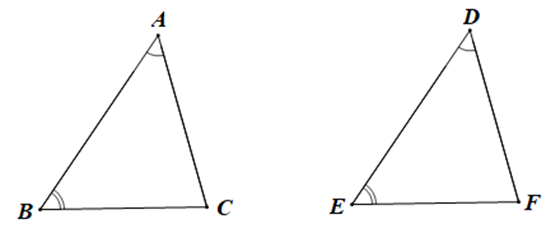
Để DABC = DDEF theo trường hợp góc – cạnh – góc mà ˆA=ˆD,ˆB=ˆE nên điều kiện còn thiếu là điều kiện về cạnh, sao cho hai cặp góc bằng nhau là hai cặp góc kề với cặp cạnh này, đó là AB = DE.
Vậy ta chọn phương án A.
Câu 3:
Cho hình vẽ dưới đây:
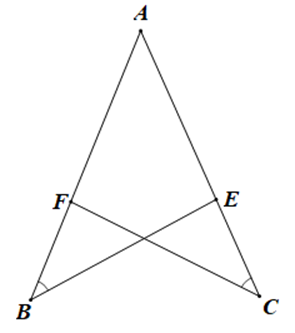
Biết ^ABE=^ACF. Cần thêm điều kiện nào sau đây để DABE = DACF theo trường hợp góc – cạnh – góc:
Xem đáp án
Đáp án đúng là: B
Để ABE = DACF theo trường hợp góc – cạnh – góc với ^ABE=^ACF và ˆA chung thì cần thêm điều kiện về cạnh, sao cho hai cặp góc bằng nhau ở trên là hai góc kề của cặp cạnh đó.
Do đó điều điện cần thêm là AB = AC.
Vậy ta chọn phương án B.
Câu 4:
Cho hình vẽ dưới đây:
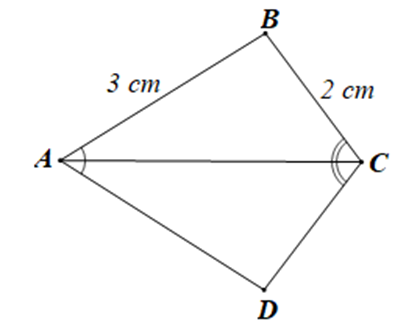
Độ dài đoạn thẳng CD bằng:
Xem đáp án
Đáp án đúng là: B
Xét tam giác ABC và tam giác ADC có:
^BAC=^DAC (giả thiết),
AC là cạnh chung,
^BCA=^DCA (giả thiết)
Do đó DABC = DADC (g.c.g)
Suy ra BC = DC (hai cạnh tương ứng)
Mà BC = 2 cm, do đó DC = 2 cm.
Vậy ta chọn phương án B.
Câu 5:
Xem đáp án
Đáp án đúng là: B
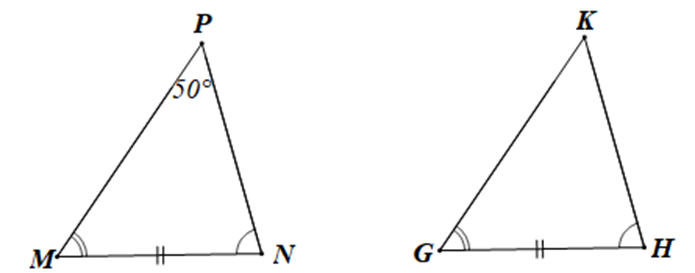
Xét tam giác MNP và tam giác GHK có:
ˆM=ˆG (giả thiết),
MN = GH (giả thiết),
ˆN=ˆH (giả thiết),
Do đó DˆP=ˆKMNP = DGHK (g.c.g)
Suy ra (hai góc tương ứng)
Mà ˆP=50∘ (giả thiết), do đó ˆK=50∘.
Vậy ta chọn phương án B.
Câu 6:
Cho tam giác DEG và tam giác HKI có ˆD=ˆK,ˆE=ˆI, DE = KI. Biết ˆD+ˆE=100∘, số đo góc H là:
Xem đáp án
Đáp án đúng là: B
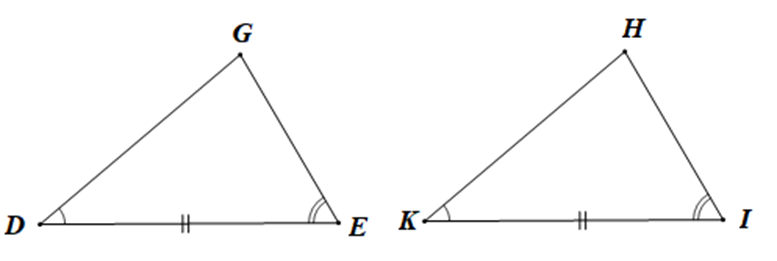
Xét DDEG và DHKI có:
ˆD=ˆK (giả thiết),
DE = KI (giả thiết),
ˆE=ˆI(giả thiết),
Do đó DDEG và DKIH (g.c.g)
Suy ra ˆG=ˆH (hai góc tương ứng)
Ta lại có: ˆD+ˆE+ˆG=180∘ (tổng ba góc trong tam giác DEG)
Suy ra ˆG=180∘−(ˆD+ˆE)=180∘−100∘=80∘
Vậy ˆH=80∘.
Câu 7:
Cho tam giác ADK nhọn. Qua A kẻ đường thẳng song song với DK, qua D kẻ đường thẳng song song với AK, hai đường thẳng này cắt nhau tại B. Khẳng định nào sau đây là sai:
Xem đáp án
Đáp án đúng là: C
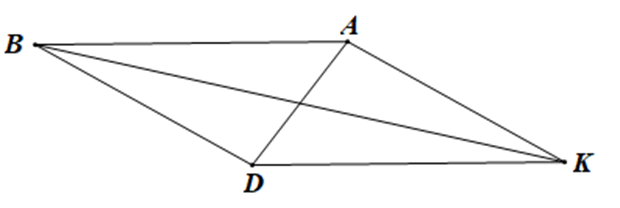
Vì AB // DK nên ^BAD=^KDA(hai góc so le trong)
Vì DB // AK nên ^KAD=^BDA (hai góc so le trong)
Xét DABD và DDKA có:
^BAD=^KDA(chứng minh trên),
AD là cạnh chung,
^BDA=^KAD (chứng minh trên)
Do đó DABD = DDKA (g.c.g)
Suy ra ^ABD=^DKA (hai góc tương ứng)
Chứng minh tương tự ta cũng có: DABK = DDKB (g.c.g)
Suy ra ^BAK=^KDB (hai góc tương ứng)
Vậy ta chọn phương án C.
Câu 8:
Cho hình vẽ dưới đây:
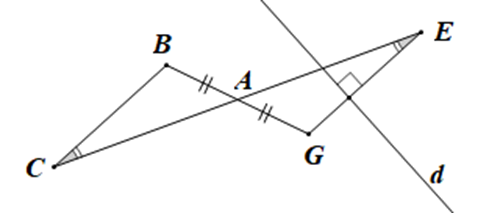
Xét các khẳng định:
(1) BC = EG;
(2) d ^ BC.
Chọn câu đúng:
Xem đáp án
Đáp án đúng là: C
Ta có: ^ACB=^AEG mà hai góc này ở vị trí so le trong nên CB // EG (dấu hiệu nhận biết)
Do đó ^ABC=^AGE (hai góc so le trong)
Xét DABC và DAGE có:
^ABC=^AGE (chứng minh trên),
AB = AG (giả thiết),
^BAC=^GAE (hai góc đối đỉnh)
Do đó DABC = DAGE (g.c.g)
Suy ra BC = GE (hai cạnh tương ứng)
Ta lại có CB // GE (chứng minh trên) mà d ^ GE (giả thiết)
Do đó d ^ CB.
Vậy ta chọn phương án C.
Câu 9:
Cho góc xOy khác góc bẹt. Trên tia phân giác của góc xOy lấy điểm M tuỳ ý, qua M vẽ đường thẳng vuông góc với OM, cắt Ox ở H và cắt Oy ở G. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án đúng là: D
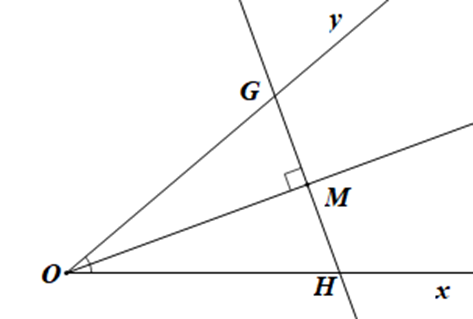
Xét DOMG và DOMH có:
^GOM=^HOM (OM là tia phân giác của ^xOy),
OM là cạnh chung,
^OMG=^OMH(=90∘),
Do đó DOMG = DOMH (g.c.g)
Suy ra:
+) OG = OH, MG = MH (các cặp cạnh tương ứng)
+) ^MGO=^MHO (hai góc tương ứng)
Vậy ta chọn phương án D.
Câu 10:
Cho tứ giác ABCD, AB // DC, AB = DC, O là giao điểm của AC và BC. Khẳng định nào sau đây là đúng:
Xem đáp án
Đáp án đúng là: C
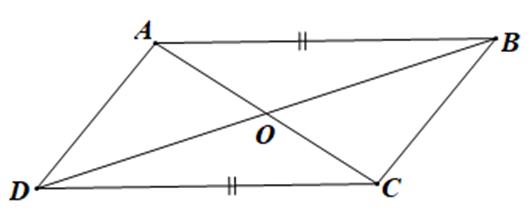
Vì AB // CD (giả thiết) nên ^BAC=^DCA và ^ABD=^CDB (các cặp góc so le trong)
Xét DOAB và DOCD có:
^BAO=^DCO (do ^BAC=^DCA),
AB = CD (giả thiết),
^ABO=^CDO (do ^ABD=^CDB)
Do đó DOAB = DOCD (g.c.g)
Suy ra OA = OC và OB = OD (các cặp cạnh tương ứng)
Xét DAOD và DCOB có:
OA = OC (chứng minh trên),
^AOD=^COB (hai góc đối đỉnh),
OD = OB (chứng minh trên)
Do đó DAOD = DCOB (g.c.g)
Suy ra AD = CB (hai cạnh tương ứng)
Vậy ta chọn phương án C.