Trắc nghiệm Toán 11 Bài 4: Hai mặt phẳng vuông góc có đáp án (Mới nhất)
Trắc nghiệm Toán 11 Bài 4: Hai mặt phẳng vuông góc có đáp án (Mới nhất)
-
266 lượt thi
-
35 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 3:
 Xem đáp án
Xem đáp án
Câu 7:
Cho hai mặt phẳng và vuông góc với nhau và gọi
I. Nếu và thì
II. Nếu thì
III. Nếu thì hoặc
IV. Nếu thì và
Các mệnh đề đúng là :
 Xem đáp án
Xem đáp án
Chọn D.
Câu 8:
 Xem đáp án
Xem đáp án
Câu 9:
 Xem đáp án
Xem đáp án
Câu 11:
Cho hai mặt phẳng (P) và (Q) song song với nhau và một điểm M không thuộc (P) và (Q). Qua M có bao nhiêu mặt phẳng vuông góc với (P) và (Q)?
 Xem đáp án
Xem đáp án
Qua M dựng đường thẳng d vuông cóc với (P) và (Q). Khi đó có vô số mặt phẳng xoay quanh d thỏa yêu cầu bài toán.
Câu 16:
 Xem đáp án
Xem đáp án
Chọn C.
Câu 18:
 Xem đáp án
Xem đáp án
Chọn A
Giả sử AB là đoạn vuông góc chung của a và b thì mà
Câu 19:
 Xem đáp án
Xem đáp án
Chọn C
Do nênCâu 20:
 Xem đáp án
Xem đáp án
Câu A sai vì a, b có thể trùng nhau.
Câu C sai vì khi a, b cắt nhau, mặt phẳng (a, b) không vuông góc với a
Câu D sai vì khi a, b chéo nhau và vuông góc với nhau, ta gọi là mặt phẳng chứa a , song song với b và là mặt phẳng chứa b và song song với a thì
Câu 21:
 Xem đáp án
Xem đáp án
Chọn đáp án D
Mệnh đề A sai vì có thể xảy ra trường hợp hai mặt phẳng vuông góc với nhau nhưng đường thẳng thuộc mặt phẳng này song song với mặt phẳng kia.
Mệnh đề B sai vì xảy ra trường hợp hai mặt phẳng song song.
Mệnh đề C sai vì xảy ra trường hợp hai mặt phẳng vuông góc.
Câu 22:
 Xem đáp án
Xem đáp án
Mệnh đề sai vì còn trường hợp chéo nhau hoặc trùng nhau.
Mênh đề C sai vì còn trường hợp hai đường thẳng chéo nhau.
Mênh đề D sai vì còn trường hợp hai mặt phẳng vuông góc với nhau.
Câu 23:
 Xem đáp án
Xem đáp án
Chọn D
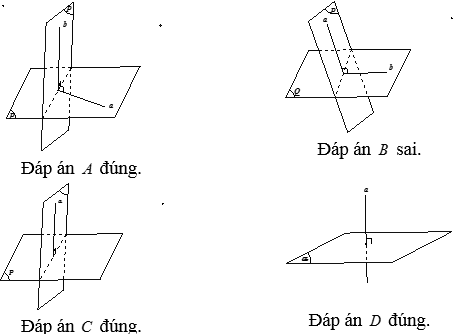
* Có vô số đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước, chúng nằm trong mặt phẳng đi qua điểm đó và vuông góc với một đường thẳng cho trước => “Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước”: SAI
* Có vô số mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước, trong trường hợp: đường thẳng cho trước vuông góc với mặt phẳng cho trước => "Có duy nhất một mặt phẳng đi qua một đường thẳng cho trước và vuông góc với một mặt phẳng cho trước”: SAI
* Có vố số mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước => ”Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước”: SAI
Câu 24:
Cho hình chóp S.ABC có đường cao SH. Xét các mệnh đề sau:
(I) SA = SB = SC
(II) H trùng với tâm đường tròn ngoại tiếp tam giác ABC .
(III) Tam giác ABC là tam giác đều.
(IV) H là trực tâm tam giác ABC .
Các yếu tố nào chưa đủ để kết luận S.ABC là hình chóp đều? Xem đáp án
Xem đáp án
Câu 25:
 Xem đáp án
Xem đáp án
Chọn A
Câu 26:
 Xem đáp án
Xem đáp án
Chọn D.
A. Vì lăng trụ đều nên các cạnh bằng nhau. Do đó đáy là đa giác đều.
B. Vì lăng trụ đều là lăng trụ đứng nên các mặt bên vuông góc với đáy.
C. Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên vuông góc với đáy.
D. Vì lăng trụ đều là lăng trụ đứng nên các cạnh bên bằng nhau và cùng vuông góc với đáy. Do đó các mặt bên là những hình vuông.
Câu 28:
 Xem đáp án
Xem đáp án
Chọn B
A sai vì đáy có thể là hình bình hành.
B đúng
C sai vì đáy có thể là hình bình hành
D sai vì đáy có thể là hình bình hành.
Câu 30:
 Xem đáp án
Xem đáp án
Chọn C
Câu 31:
 Xem đáp án
Xem đáp án
Chọn A
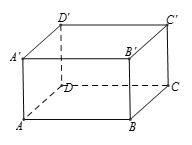
Ta có suy ra Hình hộp ABCD.A'B'C'D' là hình lập phương.
Câu 33:
 Xem đáp án
Xem đáp án
Chọn A
Câu 34:
 Xem đáp án
Xem đáp án
Chọn D
Giả sử lăng trụ ABC.A'B'C' có các mặt bên (AA'B'B), (AA'C'C) là hình chữ nhật, khi đó ta có . Vậy ABC.A'B'C' là lăng trụ đứng.
Theo định nghĩa hình chóp đều và hình lăng trụ đều ta có đáp án B, C đúng.
Đáp án D sai.
Câu 35:
 Xem đáp án
Xem đáp án
Chọn A
Áp dụng hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.