38 câu hỏi trắc nghiệm thuộc Dạng 1: Góc giữa hai mặt phẳng có đáp án

Câu 1:

Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (ABC) và (ABD) là $\hat{C B D}$

B. Góc giữa hai mặt phẳng (ACD) và (BCD) là $\hat{A I B}$

C. $(B C D) ⊥ (A I B)$

D. $(A C D) ⊥ (A I B)$

Xem đáp án

Chọn A

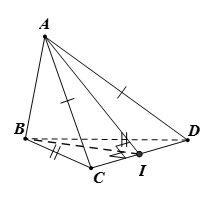
Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai? (ảnh 1)

Tam giác BCD cân tại B có I trung điểm đáy CD => $C D ⊥ B I$ (1)

Tam giác ACD cân tại A có I trung điểm đáy CD => $C D ⊥ A I$ (2)

(1) và (2) =>

C D ⊥ (A B I)

Vậy A: sai

Câu 2:

Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc

\hat{A} = 60^{0}

, cạnh

S C = \frac{a \sqrt{6}}{2}

và SC vuông góc với mặt phẳng (ABCD). Trong tam giác SAC kẻ

I K ⊥ S A

tại K . Tính số đo góc

\hat{BKD}

A. 60°

B. 45°

C. 90°

D. 30°

Xem đáp án

Chọn C

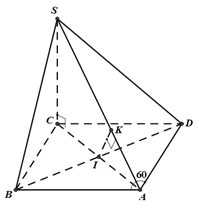
Cho hình chóp tứ giác S.ABCD, có đáy ABCD là hình thoi tâm I cạnh bằng A và góc A= 60 độ, cạnh SC = a căn bậc hai 6/2 và SC vuông góc với mặt phẳng (ABCD). (ảnh 1)

Ta có $C H = \frac{C S . C A}{\sqrt{C S^{2} + C A^{2}}} = a; (C A = 2 A I = a \sqrt{3}); I K = \frac{1}{2} C H = \frac{1}{2} a = I B = I D$

với H là hình chiếu của C lên SA, K là hình chiếu của I lên SA.

Câu 3:

Cho tứ diện đều ABCD. Góc giữa (ABC) và (ABD) bằng a . Chọn khẳng định đúng trong các khẳng định sau?

A. $\cos α = \frac{1}{3}$

B. $\cos α = \frac{1}{4}$

C. $α = 60^{0}$

D. $\cos α = \frac{1}{5}$

Xem đáp án

Chọn A

Đặt AB = a. Gọi I là trung điểm của AB

Tam giác ABC đều cạnh a nên $C I ⊥ A B$ và $C I = \frac{a \sqrt{3}}{2}$

Tam giác ABD đều nên $D I ⊥ A B$ và $D I = \frac{a \sqrt{3}}{2}$

Do đó, $((A B C), (A B D)) = (C I, D I) = \hat{C I D} = α$

Tam giác CID có

\cos α = \frac{I C^{2} + I D^{2} - C D^{2}}{2. I C . I D} = \frac{\frac{3 a^{2}}{4} + \frac{3 a^{2}}{4} - a^{2}}{2. \frac{a \sqrt{3}}{2} . \frac{a \sqrt{3}}{2}} = \frac{\frac{a^{2}}{2}}{\frac{3 a^{2}}{2}} = \frac{1}{3}

Câu 4:

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và một mặt đáy.

A. $\frac{1}{2}$

B. $\frac{1}{3}$

C. $\frac{1}{\sqrt{3}}$

D. $\frac{1}{\sqrt{2}}$

Xem đáp án

Chọn C

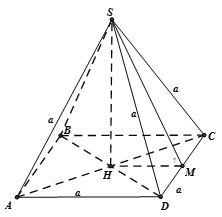
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a . Tính cosin của góc giữa một mặt bên và một mặt đáy. (ảnh 1)

Giả sử gọi hình chóp tứ giác đều có tất cả các cạnh đều bằng a là S.ABCD có đường cao SH

Ta có: $(S C D) \cap (A B C D) = C D$ . Gọi M là trung điểm CD

Dễ chứng minh được $S M ⊥ C D$ và $H M ⊥ C D$

$\Rightarrow ((S C D), (A B C D)) = (S M, H M) = \hat{S M H} = α$

Từ giả thiết suy ra tam giác SCD là tam giác đều cạnh a có SM là đường trung tuyến .

$\Rightarrow S M = \frac{a \sqrt{3}}{2} \Rightarrow \cos α = \frac{H M}{S M} = \frac{\frac{a}{2}}{\frac{a \sqrt{3}}{2}} = \frac{1}{\sqrt{3}}$

Câu 5:

Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH

(H \in B C)

. Gọi O là hình chiếu vuông góc của A lên (SBC). Khẳng định nào sau đây sai ?

A. $S C ⊥ (A B C)$

B. $O \in S H$

C. $(S A H) ⊥ (S B C)$

D. $(\hat{(S B C), (A B C)}) = \hat{S B A}$

Xem đáp án

Chọn D

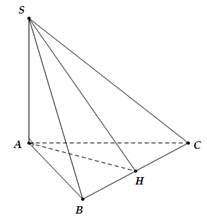
Cho hình chóp S.ABC có hai mặt bên (SAB) và (SAC) vuông góc với mặt phẳng (ABC), tam giác ABC vuông cân ở A và có đường cao AH H thuộc BC (ảnh 1)

Ta có $\begin{array}{l} (S A B) ⊥ (A B C) \\ (S A C) ⊥ (A B C) \\ (S A B) \cap (S A C) = S A \end{array}\} \Rightarrow S A ⊥ (A B C) \Rightarrow S A ⊥ B C$

$\begin{array}{l} B C ⊥ A H \\ B C ⊥ S A \end{array}\} \Rightarrow B C ⊥ (S A H) \Rightarrow B C ⊥ S H$

Mặt khác,

A H ⊥ B C

nên

((S B C), (A B C)) = (S H, A H) = \hat{S H A}

Câu 6:

Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc $\hat{B A D} = 60^{0}$ . Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) và $S O = \frac{3 a}{4}$ . Gọi E là trung điểm BC và F là trung điểm BE . Góc giữa hai mặt phẳng (SOF) và (SBC) là

A. 90°

B. 60°

C. 30°

D. 45°

Xem đáp án

Chọn A

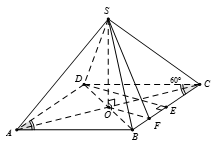
Cho hình chóp S.ABCD có đáy là hình thoi tâm O cạnh a và có góc BAD = 60 độ . Đường thẳng SO vuông góc với mặt phẳng đáy (ABCD) (ảnh 1)

Tam giác BCD đều nên $D E ⊥ B C$ . Mặt khác $O F // D E \Rightarrow B C ⊥ O F$ (1).

Do $S O ⊥ (A B C D) \Rightarrow B C ⊥ S O$ (2).

Từ (1) và (2), suy ra $B C ⊥ (S O F) \Rightarrow (S B C) ⊥ (S O F) .$

Vậy, góc giữa (SOF) và (SBC) bằng $90^{o} .$

Câu 7:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng

A. 30°

B. 90°

C. 60°

D. 45°

Xem đáp án

Chọn B

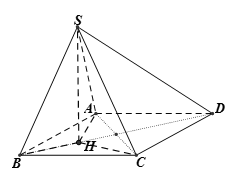
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và có SA = SB = SC = a . Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng (ảnh 1)

Gọi H là chân đường vuông góc của S xuống mặt phẳng đáy (ABCD) ( $S H ⊥ (A B C D)$ )

$S A = S B = S C = a$ => các hình chiếu: $H A = H B = H C$ => H là tâm đường tròn (ABC)

Mà tam giác ABC cân tại B (vì BA = BC = a ) => tâm H phải nằm trên BH => $S H \subset (S B D)$

Vậy có

\begin{array}{l} S H ⊥ (A B C D) \\ S H \subset (S B D) \end{array}\} \Rightarrow (S B D) ⊥ (A B C D)

nên góc

[(S B D), (A B C D)] = 90^{o}

Câu 8:

Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . Góc giữa hai mặt phẳng (MBD) và (ABCD) bằng:

A. 90°

B. 60°

C. 45°

D. 30°

Xem đáp án

Chọn C

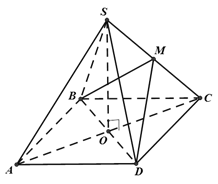
Cho hình chóp tứ giác đều S.ABCD , có đáy ABCD là hình vuông tâm O. Các cạnh bên và các cạnh đáy đều bằng a . Gọi M là trung điểm SC . (ảnh 1)

Gọi M' là trung điểm OC. Có:

$S_{Δ M B D} = \frac{1}{2} M O . B D = \frac{1}{2} . \frac{a}{2} . a \sqrt{2} = \frac{a^{2} \sqrt{2}}{4} S_{Δ B M^{'} D} = \frac{1}{2} M^{'} O . B D = \frac{1}{2} . \frac{1}{4} . a \sqrt{2} . a \sqrt{2} = \frac{a^{2}}{4}$

Do đó $\cos α = \frac{S_{Δ B M^{'} D}}{S_{Δ B M D}} = \frac{\sqrt{2}}{2} \Rightarrow α = 45^{0}$

Câu 9:

Cho tam giác ABCC vuông tại A . Cạnh AB = a nằm trong mặt phẳng (P) , cạnh

A C = a \sqrt{2}

, AC tạo với (P) một góc 60^o . Chọn khẳng định đúng trong các khẳng định sau?

A. (ABC) tạo với (P) góc 45^o

B. BC tạo với (P) góc 30^o

C. BC tạo với (P) góc 45^o

D. BC tạo với (P) góc

60^{o}

Xem đáp án

Chọn C

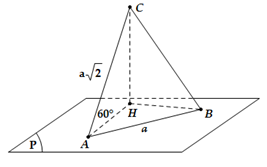
Cho tam giác ABCC vuông tại A . Cạnh AB = a nằm trong mặt phẳng (P) , cạnh AC = a căn bậc hai 2, AC tạo với (P) một góc 60 độ (ảnh 1)

Gọi H là hình chiếu vuông góc của C lên mặt phẳng (P)

Khi đó, $(A C, (P)) = (A C, A H) = \hat{C A H} = 60^{0}$ và $(B C, (P)) = (B C, A H) = \hat{C B H} = α$

Tam giác AHC vuông tại H nên $\sin \hat{C A H} = \frac{C H}{A C} \Rightarrow C H = A C . \sin \hat{C A H} = a \sqrt{2} . \sin 60^{0} = \frac{a \sqrt{6}}{2}$

Tam giác CHB vuông tại H nên

\sin α = \frac{C H}{B C} = \frac{\frac{a \sqrt{6}}{2}}{\sqrt{a^{2} + {(a \sqrt{2})}^{2}}} = \frac{a \sqrt{2}}{2} \Rightarrow α = 45^{0}

Câu 10:

Cho hình chóp S.ABC có

S A ⊥ (A B C)

và đáy ABC vuông ở A. Khẳng định nào sau đây sai ?

A.

(S A B) ⊥ (A B C)

B.

(S A B) ⊥ (S A C)

C. Vẽ

A H ⊥ B C, H \in B C \Rightarrow

góc AHS là góc giữa hai mặt phẳng (SBC) và (ABC)

D. Góc giữa hai mặt phẳng (SBC) và (SAC) là góc

\hat{S C B}

Xem đáp án

Chọn D

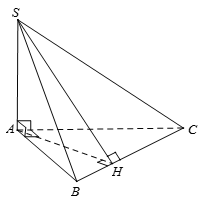
Cho hình chóp S.ABC có SA vuông góc (ABC) và đáy ABC vuông ở A. Khẳng định nào sau đây sai ? (ảnh 1)

Ta có $S A ⊥ (A B C) \Rightarrow (S A B) ⊥ (A B C)$ nên đáp án A đúng.

$A B ⊥ A C, A B ⊥ S A \Rightarrow A B ⊥ (S A C) \Rightarrow (S A B) ⊥ (S A C)$ . Nên đáp án B đúng

A H ⊥ B C; B C ⊥ S A \Rightarrow B C ⊥ (S A H) \Rightarrow S H ⊥ B C \Rightarrow (\hat{(S B C), (A B C)}) = \hat{S H A}

. Nên đáp án C đúng.

Ta có: $(S B C) \cap (S A C) = S C$ nên đáp án D sai.

Câu 11:

Cho tứ diện ABCD có AC = AD và BC = BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai ?

A. Góc giữa hai mặt phẳng (ACD) và (BCD) là góc $\hat{A I B}$

B. $(B C D) ⊥ (A I B)$

C. Góc giữa hai mặt phẳng (ABC) và (ABD) là góc $\hat{C B D}$

D. $(A C D) ⊥ (A I B)$

Xem đáp án

Chọn C

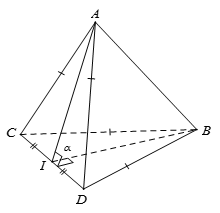
Ta có: $\{\begin{matrix} (A B C) \cap (A B D) = A B \\ B C ⊥ A B \\ B D ⊥ A B \end{matrix}$

$\Rightarrow \hat{((A B D), (A B C))} \neq \hat{C B D}$

Nên đáp án C sai

Câu 12:

Cho hình chóp S.ABC có

S A ⊥ (A B C)

và

A B ⊥ B C

, gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?

A. Góc SBA

B. Góc SCA

C. Góc SCB

D. Góc SIA

Xem đáp án

Chọn A

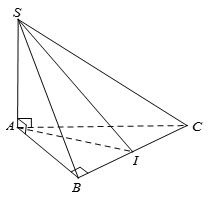
Cho hình chóp S.ABC có SA vuông góc mp ABC và AB vuông góc BC, gọi I là trung điểm BC. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây? (ảnh 1)

Ta có: $B C ⊥ S A, B C ⊥ A B \Rightarrow B C ⊥ S B \Rightarrow \{\begin{matrix} (S B C) \cap (A B C) = B C \\ A B ⊥ B C, A B \subset (A B C) \\ S B ⊥ B C, S B \subset (S B C) \end{matrix} \Rightarrow \hat{((S B C), (A B C))} = \hat{S B A}$

Câu 13:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và $S A ⊥ (A B C D)$ , gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc

\hat{A B S}

B. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc

\hat{S O A}

C. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc

\hat{S D A}

D.

(S A C) ⊥ (S B D)

Xem đáp án

Chọn C

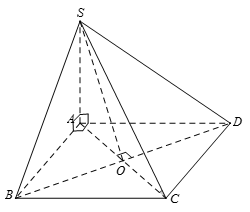
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc mp ABCD, gọi O là tâm hình vuông ABCD. Khẳng định nào sau đây sai? (ảnh 1)

Ta có:

$\{\begin{matrix} (S A D) \cap (A B C D) = A D \\ A B ⊥ A D, A B \subset (A B C D) \\ S A ⊥ A D, S A \subset (S A D) \end{matrix} \Rightarrow \hat{((S A D), (A B C D))} = \hat{S A B}$

Câu 14:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết

S O ⊥ (A B C D)

,

S O = a \sqrt{3}

và đường tròn ngoại tiếp ABCD có bán kính bằng a. Gọi

α

là góc hợp bởi mặt bên (SCD) với đáy. Khi đó

\tan α = ?

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{3}}{\sqrt{2}}$

C. $\frac{\sqrt{6}}{6}$

D. $\sqrt{6}$

Xem đáp án

Chọn D

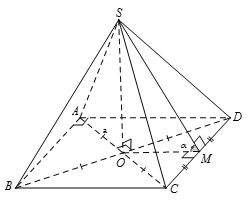
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O. Biết SO vuông góc mp ABCD, SO a căn bậc hai 3 và đường tròn ngoại tiếp ABCD (ảnh 1)

Gọi M là trung điểm của CD

Khi đó $\{\begin{matrix} C D ⊥ O M \\ C D ⊥ S O \end{matrix}$

$\Rightarrow C D ⊥ S M \Rightarrow \hat{((S C D), (A B C D))} = \hat{S M O} = α$

Ta có: $R = O A = a \Rightarrow A C = 2 a \Rightarrow A B = A D = a \sqrt{2}$

$\Rightarrow O M = \frac{a \sqrt{2}}{2} \Rightarrow \tan α = \frac{S O}{O M} = \sqrt{6}$

Câu 15:

Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng

α

Chọn khẳng định đúng trong các khẳng định sau?

A. $α = 6 0^{0}$

B. $\cos α = \frac{1}{3 \sqrt{5}}$

C. $\cos α = \frac{1}{4 \sqrt{5}}$

D. $\cos α = \frac{1}{2 \sqrt{5}}$

Xem đáp án

Chọn B

Cho hình chóp tam giác đều S.ABC với SA = 2AB. Góc giữa (SAB) và (ABC) bằng anpha Chọn khẳng định đúng trong các khẳng định sau? (ảnh 1)

Gọi O là tâm của tam giác đều ABC

Gọi $C O \cap A B = H$ suy ra H là trung điểm AB(vì tam giác ABC đều)

$\Rightarrow O H ⊥ A B$ và $O H = \frac{1}{3} C H = \frac{1}{3} . \frac{A B \sqrt{3}}{2} = \frac{A B \sqrt{3}}{6}$

Tìm góc giữa (SAB) và (ABC)

$\{\begin{matrix} (S A B) \cap (A B C) = A B \\ O H ⊥ A B \\ S O ⊥ A B (S O ⊥ (A B C)) \end{matrix}$

$\Rightarrow S H ⊥ A B$ (1)

Ta có

$\{\begin{matrix} (S A B) \cap (A B C) = A B \\ O H ⊥ A B, O H \subset (A B C) \\ S H ⊥ A B, S H \subset (S A B) \end{matrix} \Rightarrow (\hat{(S A B); (A B C)}) = (\hat{S H; O H}) = \hat{S H O} = α$

Từ (1) suy ra $S H = \sqrt{S A^{2} - A H^{2}} = \sqrt{{(2 A B)}^{2} - {(\frac{A B}{2})}^{2}} = \frac{\sqrt{15}}{2} A B$

Từ đó ta có : $\cos α = \frac{O H}{S H} = \frac{\frac{\sqrt{3}}{6} A B}{\frac{\sqrt{15}}{2} A B} = \frac{1}{3 \sqrt{5}}$

Câu 16:

Cho tam giác cân ABC có đường cao

A H = a \sqrt{3}

,

B C = 3 a

chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A'BC vuông tại A'. Gọi

φ

là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau?

A.

Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 6)

B.

Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 7)

C.

Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 8)

D.

Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 9)

Xem đáp án

Chọn D

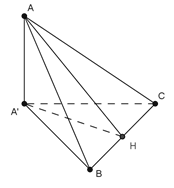
Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 1)

Ta có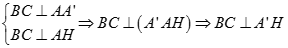

Do đó:

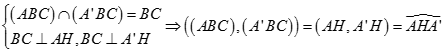
Cho tam giác cân ABC có đường cao AH = a căn bậc hai 3, BC = 3a chứa trong mặt phẳng (P). Gọi A' là hình chiếu vuông góc của A lên mặt phẳng (P). (ảnh 3)

Mặt khác, tam giác A'BC vuông tại A' nên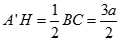

Ta có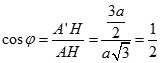

Câu 17:

Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H , K lần lượt là trung điểm của AB, CD. Ta có tan của góc tạo bởi hai mặt phẳng (SAB) và (SCD) bằng :

A. $\frac{\sqrt{2}}{3}$

B. $\frac{2 \sqrt{3}}{3}$

C. $\frac{\sqrt{3}}{3}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Chọn B

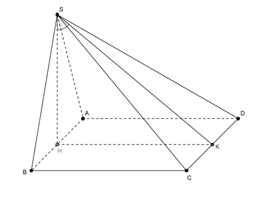
Trong không gian cho tam giác đều SAB và hình vuông ABCD cạnh a nằm trên hai mặt phẳng vuông góc. Gọi H , K lần lượt là trung điểm của AB, CD. (ảnh 1)

Ta có: $S \in (S A B) \cap (S C D)$

Gọi $d = (S A B) \cap (S C D)$ với $d \in S; d ∥ A B ∥ C D$

Do đó: $d = (S A B) \cap (S C D)$

Mặt khác: $(S A B) ⊥ (A B C D)$ ; mà $H K ⊥ A B (h v) \Rightarrow H K ⊥ (S A B)$

Vì là trung điểm của AB $\Rightarrow S H ⊥ A B \Rightarrow S H ⊥ d$ (vì d // AB)

$\Rightarrow d ⊥ S K$ (theo định lí ba đường vuông góc)

Do đó: $\hat{K S H} = α$ là góc giữa (SAB) và (SCD)

Mà SH là đường cao trong $Δ S A B$ đều cạnh $a \Rightarrow S H = \frac{a \sqrt{3}}{2}$

Xét vuông tại có: $\tan α = \frac{H K}{S H} = \frac{a}{\frac{a \sqrt{3}}{2}} = \frac{2 \sqrt{3}}{3}$

Câu 18:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng

\frac{2 a}{\sqrt{5}}

. Biết

S A ⊥ (A B C D)

và SA = 2a . Gọi

α

là góc giữa hai mặt phẳng (ABCD) và (SBD). Khẳng định nào sau đây sai?

A. $(S A B) ⊥ (S A D)$

B. $(S A C) ⊥ (A B C D)$

C. $\tan α = \sqrt{5}$

D. $α = \hat{S O A}$

Xem đáp án

Chọn D

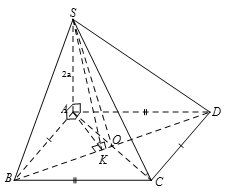
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và khoảng cách từ A đến BD bằng 2a/ căn bậc hai 5 . Biết SA vuông góc mp ABCD và SA = 2a . (ảnh 1)

Gọi AK là khoảng cách từ A đến BD

Khi đó $A K = \frac{2 a}{\sqrt{5}}$ và $B D ⊥ A K, B D ⊥ S A$

$\hat{((S B D), (A B C D))} = \hat{S K A} = α \Rightarrow \tan α = \frac{S A}{A K} = \sqrt{5} .$

Câu 19:

Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ?

A. Các mặt bên của hình lăng trụ là các hình chữ nhật.

B. Góc giữa hai mặt phẳng (AA'C'C) và (BB'D'D) có số đo bằng 60^o

C. Hai mặt bên (AA'C) và (BB'D) vuông góc với hai đáy.

D. Hai hai mặt bên (AA'B'B) và (AA'D'D) bằng nhau.

Xem đáp án

Chọn B

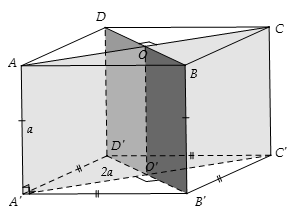
Cho hình lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, AC = 2a. Các cạnh bên vuông góc với đáy và AA' = a. Khẳng định nào sau đây sai ? (ảnh 1)

Ta có: các cạnh bên vuông góc với đáy, đáy là hình thoi nên các mặt bên của hình lăng trụ là các hình chữ nhật.

Hai mặt bên (AA'C) và (BB'D) vuông góc với hai đáy.

Hai hai mặt bên (AA'B'B) và (AA'D'D) bằng nhau.

suy ra đáp án A,C,D đúng.

Mặt khác hai đáy ABCD và A'B'C'D' là các hình thoi nên $(A A^{'} C^{'} C) ⊥ (B B^{'} D^{'} D)$ . Suy ra đáp án B sai.

Câu 20:

Cho hình lập phương $A B C D . A_{1} B_{1} C_{1} D_{1}$ . Gọi $α$ là góc giữa hai mặt phẳng (A₁D₁CB) và (ABCD). Chọn khẳng định đúng trong các khẳng định sau?

A. $α = 45^{0}$

B. $α = 30^{0}$

C. $α = 60^{0}$

D. $α = 90^{0}$

Xem đáp án

Chọn A

$α$ là góc giữa hai mặt phẳng (A₁D₁CB) và (ABCD) là $α = \hat{M N P}$

Ta có $\tan α = \frac{M P}{N P} = 1 \Rightarrow α = 45^{0}$

Câu 21:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và $S A ⊥ (A B C D)$ . Khẳng định nào sau đây sai ?

A. Góc giữa hai mặt phẳng (SBC) và (ABCD) là góc

\hat{A B S}

B.

(S A C) ⊥ (S B D)

C. Góc giữa hai mặt phẳng (SBD) và (ABCD) là góc

\hat{S O A}

D. Góc giữa hai mặt phẳng (SAD) và (ABCD) là góc

\hat{S D A}

Xem đáp án

Chọn D

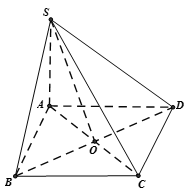
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có tâm O và SA vuông góc mp ABCD. Khẳng định nào sau đây sai ? (ảnh 1)

Ta có: $(S B C) \cap (A B C D) = C D$

$\{\begin{cases} A B ⊥ B C, A B \subset (A B C D) \\ S B ⊥ B C, S B \subset (S B C) \end{cases}$

$\Rightarrow (\hat{(S B C); (A B C D)}) = \hat{A B S}$ . Vậy A đúng

Ta có: $\{\begin{cases} B D ⊥ A C \\ B D ⊥ S A \end{cases} \Rightarrow B D ⊥ (S A C)$

Mà $B D \subset (S B D) \Rightarrow (S A C) ⊥ (S B D)$ . Vậy B đúng

Ta có: $(S B D) \cap (A B C D) = B D$

$\{\begin{cases} A O ⊥ B D, A B \subset (A B C D) \\ S O ⊥ B D, S O \subset (S B D) \end{cases}$

$\Rightarrow (\hat{(S B D); (A B C D)}) = \hat{S O A}$ . Vậy C đúng

Ta có: $(S A D) \cap (A B C D) = B D$

$\{\begin{cases} A B ⊥ A D, A B \subset (A B C D) \\ S A ⊥ A D, S A \subset (S A D) \end{cases}$

\Rightarrow (\hat{(S A D); (A B C D)}) = \hat{S A B} = 90^{0}

. Vậy D sai.

Câu 22:

Tính cosin của góc giữa hai mặt của một tứ diện đều.

A. $\frac{1}{3} .$

B. $\frac{1}{2} .$

C. $\frac{\sqrt{2}}{3} .$

D. $\frac{\sqrt{3}}{2} .$

Xem đáp án

Chọn A

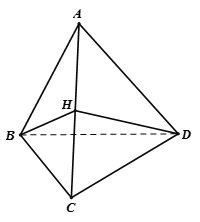
Tính cosin của góc giữa hai mặt của một tứ diện đều. A. 1/3 B. 1/2 C. căn bậc hai 2/3 D. căn bậc hai 3/2 (ảnh 1)

Gọi H là trung điểm của AC khi đó $B H ⊥ A C; D H ⊥ A C$

Góc giữa hai mặt của tứ diện bằng $\hat{B H D}$

Ta có $B H = D H = \frac{a \sqrt{3}}{2}$

Trong tam giác BHD có :

Tính cosin của góc giữa hai mặt của một tứ diện đều. A. 1/3 B. 1/2 C. căn bậc hai 2/3 D. căn bậc hai 3/2 (ảnh 2)

Câu 23:

Cho hình chóp tứ giác đều S.ABCD có SA = SB. Góc giữa (SAB) và (SAD) bằng

α

. Chọn khẳng định đúng trong các khẳng định sau?

A. $\cos α = - \frac{1}{3}$

B. $\cos α = \frac{2}{5}$

C. $α = 60^{0}$

D. $\cos α = \frac{2}{3}$

Xem đáp án

Chọn A

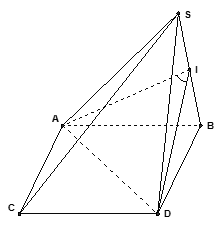
Cho hình chóp tứ giác đều S.ABCD có SA = SB. Góc giữa (SAB) và (SAD) bằng anpha. Chọn khẳng định đúng trong các khẳng định sau? (ảnh 1)

Gọi độ dài cạnh của hình chóp đều S.ABCD là a . Gọi I là trung điểm của SB ta có $D I ⊥ S B$ (vì tam giác SBD đều) và $A I ⊥ S B$ (vì tam giác SAB đều). Vậy, góc giữa hai mặt phẳng (SAB) và (SAD) chính là góc .

Ta có : $A D = a \sqrt{2}$ (đường chéo hình vuông), $A I = D I = \frac{a \sqrt{3}}{2}$ (đường cao tam giác đều)

Áp dụng định lý cosin cho góc I trong tam giác AID ta có :

$c o s (\hat{A I D}) = \frac{A I^{2} + D I^{2} - A D^{2}}{2 A D . D I} = \frac{{(\frac{a \sqrt{3}}{2})}^{2} + {(\frac{a \sqrt{3}}{2})}^{2} - {(a \sqrt{2})}^{2}}{2. (\frac{a \sqrt{3}}{2}) . (\frac{a \sqrt{3}}{2})} = - \frac{1}{3}$

Vậy $\cos α = - \frac{1}{3}$

Câu 24:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a, AD = DC = a. Cạnh bên SA vuông góc với đáy và

S A = a \sqrt{2}

. Chọn khẳng định sai trong các khẳng định sau?

A.

(S B C) ⊥ (S A C)

B. Giao tuyến của (SAB) và (SCD) song song với AB

C. (SDC) tạo với (BCD) một góc 60^o

D. (SBC) tạo với đáy một góc 45^o

Xem đáp án

Chọn C

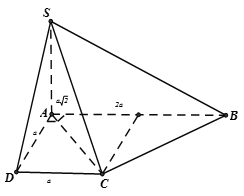
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. AB = 2a, AD = DC = a. Cạnh bên SA vuông góc với đáy và SA = a căn bậc hai 2. (ảnh 1)

Ta có: $\{\begin{cases} B C ⊥ S A \\ B C ⊥ A B \end{cases} \Rightarrow B C ⊥ (S A B)$

Mà $B C \subset (S B C) \Rightarrow (S B C) ⊥ (S A C)$ (A đúng)

$\{\begin{cases} (S A D) \cap (S A B) = S \\ A B / / C D \\ A B \subset (S A B) \\ C D \subset (S C D) \end{cases} \Rightarrow (S A D) \cap (S A B) = S x / / A B$

B đúng

$(S C D) \cap (B C D) = C D$

Ta có: $\{\begin{cases} A D ⊥ C D, A D \subset (B C D) \\ S D ⊥ C D, S D \subset (S C D) \end{cases}$

Suy ra góc giữa (SDC) và (BCD) là $\hat{S D A}$

$\tan \hat{S D A} = \frac{S A}{A D} = \sqrt{2} \Rightarrow \hat{S D A} = 54^{0} 44'$ (C sai)

Câu 25:

Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA' = a, AD = 2a. Gọi

α

là góc giữa đường chéo A'C và đáy ABCD. Tính

α

.

A. $α \approx 20 ° 45^{'}$

B. $α \approx 24 ° 5^{'}$

C. $α \approx 30 ° 18^{'}$

D. $α \approx 25 ° 48^{'}$

Xem đáp án

Chọn B

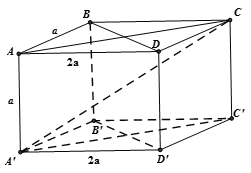
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AA' = a, AD = 2a. Gọi anpha là góc giữa đường chéo A'C và đáy ABCD. Tính anpha. (ảnh 1)

Từ giả thiết ta suy ra: $A A^{'} ⊥ (A B C D) \Rightarrow A C$ là hình chiếu vuông góc của A'C lên mặt phẳng (ABCD)

$\Rightarrow (A^{'} C, (A B C D)) = (A^{'} C, A C) = \hat{A^{'} C A} = α$

Áp dụng định lý Pytago trong tam giác ABC vuông tại B ta có:

$A C^{2} = A B^{2} + B C^{2} = a^{2} + 4 a^{2} = 5 a^{2} \Rightarrow A C = a \sqrt{5}$

Áp dụng hệ thức lượng trong tam giác AA'C vuông tại A ta có:

$\tan α = \frac{A A^{'}}{A C} = \frac{a}{a \sqrt{5}} = \frac{1}{\sqrt{5}}$ $\Rightarrow α \approx 24 ° 5^{'}$

Câu 26:

Cho hình lập phương ABCD.A'B'C'D' . Xét mặt phẳng (A'BD). Trong các mệnh đề sau mệnh đề nào đúng?

A. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng

α

mà

\tan α = \frac{1}{\sqrt{2}}

B. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng

α

mà

\sin α = \frac{1}{\sqrt{3}}

C. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các cạnh của hình lập phương phụ thuộc vào kích thước của hình lập phương.

D. Góc giữa mặt phẳng (A'BD) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.

Xem đáp án

Chọn D

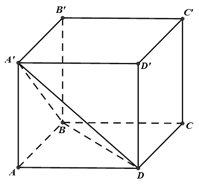
Cho hình lập phương ABCD.A'B'C'D' . Xét mặt phẳng (A'BD). Trong các mệnh đề sau mệnh đề nào đúng? (ảnh 1)

ABCD.A'B'C'D' là hình lặp phương nên hình chiếu của tam giác A'BD lên các mặt chứa các cạnh của hình lặp phương là các tam giác bằng nhau. Gọi S₁ là diện tích các tam giác này

Lại có $S_{1} = S_{A B' D} . c o s α$

Câu 27:

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy.

A. 30^o

B. 45^o

C. 60^o

D. 75^o

Xem đáp án

Chọn C

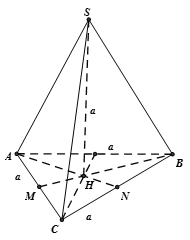
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và đường cao SH bằng cạnh đáy. Tính số đo góc hợp bởi cạnh bên và mặt đáy. (ảnh 1)

+ Vì $S H ⊥ (A B C)$ và $A N \subset (A B C) \Rightarrow S H ⊥ A N$ hay $\Rightarrow S H ⊥ A H \Rightarrow A H$ là hình chiếu vuông góc của SA lên $(A B C)$

$(S A, (A B C)) = (S A, A H) = \hat{S A H}$

+ Gọi M, N lần lượt là trung điểm của AC, BC

Vì ABC là tam giác đều cạnh nên dễ tính được : $A N = \frac{a \sqrt{3}}{2}$

Từ giả thiết suy ra H là trọng tậm $Δ A B C$ $\Rightarrow A H = \frac{2}{3} A N = \frac{2}{3} . \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{3}$

+ Áp dụng hệ thức lượng trong tam giác SHA vuông tại H ta có:

$\tan \hat{S A H} = \frac{S H}{A H} = \frac{a}{\frac{a \sqrt{3}}{3}} = \sqrt{3}$

Câu 28:

Cho hình chóp tứ giác đều có cạnh đáy bằng

a \sqrt{2}

và chiều cao bằng

\frac{a \sqrt{2}}{2}

. Tính số đo của góc giữa mặt bên và mặt đáy.

A. 30^o

B. 45^o

C. 60^o

D. 75^o

Xem đáp án

Chọn B

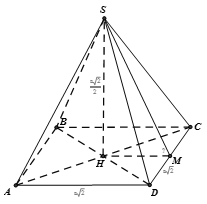
Cho hình chóp tứ giác đều có cạnh đáy bằng a căn bậc hai 2 và chiều cao bằng a căn bậc hai hai/2. Tính số đo của góc giữa mặt bên và mặt đáy. (ảnh 1)

Giả sử hình chóp đã cho là S.ABCD có đường cao SH

Ta có: $(A B C D) \cap (S C D) = C D$

Gọi M là trung điểm của CD => dễ chứng minh được $S M ⊥ C D$ và $H M ⊥ C D$

$\Rightarrow ((A B C D), (S C D)) = (H M, S M) = \hat{S M H}$

Mặt khác: $H M = \frac{1}{2} A D = \frac{a \sqrt{2}}{2}$

Áp dụng hệ thức lượng trong tam giác SHM vuông tại H, ta có :

$\tan \hat{S M H} = \frac{S H}{H M} = \frac{a \sqrt{2}}{2} . \frac{2}{a \sqrt{2}} = 1 \Rightarrow \hat{S M H} = 45 °$

Câu 29:

Tính cosin của góc giữa hai mặt của một tứ diện đều.

A. $\frac{\sqrt{3}}{2}$

B. $\frac{\sqrt{2}}{3}$

C. $\frac{1}{2}$

D. $\frac{1}{3}$

Xem đáp án

Chọn D

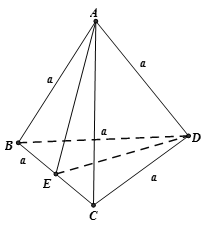
Tính cosin của góc giữa hai mặt của một tứ diện đều. A. căn bậc hai 3/2 B. căn bậc hai 2/3 C. 1/2 D. 1/3 (ảnh 1)

Giả sử tứ diện đều đã cho là ABCD có cạnh a .

Ta có: $(A B C) \cap (B C D) = B C$

Gọi E là trung điểm BC. Khi đó dễ dàng chứng minh được $A E ⊥ B C$ và $D E ⊥ B C$

$\Rightarrow ((A B C), (B C D)) = (A E, D E) = \hat{A E D}$

Ta dễ tính được: $A E = D E = \frac{a \sqrt{3}}{2}$

Áp dụng hệ quả của định lý cô sin trong tam giác AED ta có:

$\cos \hat{A E D} = \frac{A E^{2} + D E^{2} - A D^{2}}{2. A E . D E} = \frac{\frac{3 a^{2}}{4} + \frac{3 a^{2}}{4} - a^{2}}{2. \frac{a \sqrt{3}}{2} . \frac{a \sqrt{3}}{2}} = \frac{\frac{a^{2}}{2}}{\frac{3 a^{2}}{2}} = \frac{1}{3}$

Câu 30:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và

S A = a \sqrt{3}

. Gọi

φ

là góc giữa hai mặt phẳng (SBC) và (SCD). Chọn khẳng định đúng trong các khẳng định sau?

A. $\cos \frac{φ}{2} = \frac{\sqrt{10}}{4}$

B. $\cos \frac{φ}{2} = \frac{1}{4}$

C. $\sin \frac{φ}{2} = \frac{\sqrt{10}}{4}$

D. $\sin \frac{φ}{2} = \frac{1}{4}$

Xem đáp án

Chọn C

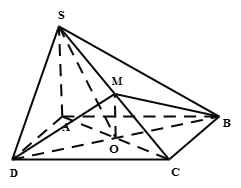
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a căn bậc hai 3. (ảnh 1)

Ta có SB = SD = 2a

Vì $Δ S C D = Δ S C B (c.c.c)$ nên chân đường cao hạ từ B và D đến SC của hai tam giác đó trùng nhau và độ dài đường cao bằng nhau $\Rightarrow B H = D H$

Do đó $\hat{((S B C), (S C D))} = \hat{D H B} = φ$

Ta có

$\begin{array}{l} O B = O D = \frac{B D}{2} = \frac{a \sqrt{2}}{2} \\ \frac{1}{B H^{2}} = \frac{1}{S B^{2}} + \frac{1}{B C^{2}} = \frac{1}{4 a^{2}} + \frac{1}{a^{2}} = \frac{5}{4 a^{2}} \Rightarrow B H = D H = \frac{2 \sqrt{5}}{5} a \end{array}$

Lại có BH = DH và O là trung điểm BD nên $H O ⊥ B D$ hay $Δ H O B$ vuông tại O

$O H = \sqrt{B H^{2} - O B^{2}} = \sqrt{{(\frac{2 \sqrt{5} a}{5})}^{2} - {(\frac{a \sqrt{2}}{2})}^{2}} = \frac{\sqrt{30}}{10} a$

Ta có $\sin \frac{φ}{2} = \frac{O H}{B H} = \frac{\frac{\sqrt{30}}{10}}{\frac{2 \sqrt{5}}{5}} = \frac{\sqrt{6}}{4}; \sin \frac{φ}{2} = \frac{O B}{B H} = \frac{\frac{\sqrt{2}}{2}}{\frac{2 \sqrt{5}}{5}} = \frac{\sqrt{10}}{4}$

Câu 31:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu?

A. 30^o

B. 45^o

C. 90^o

D. 60^o

Xem đáp án

Chọn D

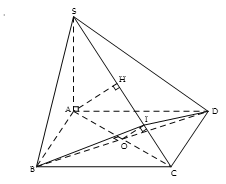
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với đáy và SA = a. Góc giữa hai mặt phẳng (SBC) và (SCD) bằng bao nhiêu? (ảnh 1)

Ta có: $S C ⊥ B D$ (vì $B D ⊥ A C, B D ⊥ S A$ )

Trong mặt phẳng (SAC), kẻ $O I ⊥ S C$ thì ta có $S C ⊥ (B I D)$

Khi đó $(\hat{(S B C), (S C D)}) = \hat{B I D}$

Trong tam giác SAC , kẻ đường cao AH thì $A H = \frac{a \sqrt{2}}{\sqrt{3}}$

Mà O là trung điểm AC và OI // AH nên $O I = \frac{a}{\sqrt{6}}$

Tam giác IOD vuông tại O có $t a n \hat{O I D} = \sqrt{3} \Rightarrow \hat{O I D} = 60^{0}$

Vậy hai mặt phẳng (SBC) và (SCD) hợp với nhau một góc 60^o

Câu 32:

Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho

A M = \frac{3 a}{4}

. Tang của góc hợp bởi hai mặt phẳng (MBC) và (ABC) là:

A. $\frac{\sqrt{2}}{2}$

B. 2

C. $\frac{1}{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Chọn D

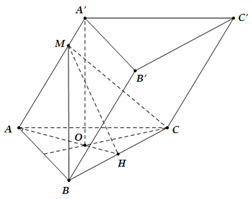
Lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy bằng a. Gọi M là điểm trên cạnh AA' sao cho AM = 3a/4. (ảnh 1)

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC . Khi đó, $A^{'} O ⊥ (A B C)$

Trong mặt phẳng (ABC) , dựng $A H ⊥ B C$ . Vì tam giác ABCD đều nên $A H = \frac{a \sqrt{3}}{2}$

Ta có $\begin{array}{l} B C ⊥ A H \\ B C ⊥ A^{'} O \end{array}\} \Rightarrow B C ⊥ (A^{'} H A) \Rightarrow B C ⊥ M H$

Do đó, $((M B C), (A B C)) = (M H, A H) = \hat{M H A} = α$

Tam giác MAH vuông tại A nên

\tan α = \frac{A M}{A H} = \frac{\frac{3 a}{4}}{\frac{a \sqrt{3}}{2}} = \frac{\sqrt{3}}{2}

Câu 33:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a.

S A ⊥ (A B C D)

, SA = x . Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60^o.

A. $x = \frac{3 a}{2}$

B. $x = \frac{a}{2}$

C. x = a

D. x = 2a

Xem đáp án

Chọn C

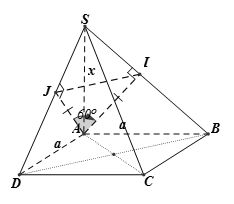
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. , SA = x . Xác định x để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc 60 độ (ảnh 1)

* Trong (SAB) dựng $A I ⊥ S B$ ta chứng minh được $A I ⊥ (S B C)$ (1)

Trong (SAD) dựng $A J ⊥ S D$ ta chứng minh được $A J ⊥ (S C D)$ (2)

Từ (1) và (2) => góc $((S B C), (S C D)) = (A I, A J) = \hat{I A J}$ o

* Ta chứng minh được AI = AJ. Do đó, nếu góc $\hat{I A J} = 60^{o}$ thì $Δ A I J$ đều $\Rightarrow A I = A J = I J$

vuông tại có là đường cao $\Rightarrow A I . S B = S A . A B \Rightarrow A I = \frac{S A . A B}{S B}$ (3)

Và có $S A^{2} = S I . S B \Rightarrow S I = \frac{S A^{2}}{S B}$ (4)

Ta chứng minh được $I J // B D \Rightarrow \frac{I J}{B D} = \frac{S I}{S B} \Rightarrow I J = \frac{S I . B D}{S B} = \frac{S A^{2} . B D}{S B^{2}}$ (5)

Thế (3) và (5) vào $A I = I J \Rightarrow A B = \frac{S A . B D}{S B} \Leftrightarrow A B . S B = S A . B D \Leftrightarrow a . \sqrt{x^{2} + a^{2}} = x . a \sqrt{2} \Leftrightarrow x^{2} + a^{2} = 2 x^{2} \Leftrightarrow x = a$

Câu 34:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết

S O ⊥ (A B C D), S O = a \sqrt{3}

và đường tròn nội tiếp ABCD có bán kính bằng a. Tính góc hợp bởi mỗi mặt bên với đáy.

A. 30^o

B. 45^o

C. 60^o

D. 75^o

Xem đáp án

Chọn C

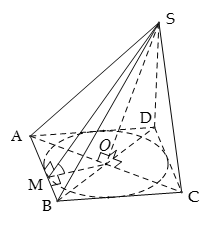
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết SO vuông góc mp ABCD, SO = a căn bậc hai 3 (ảnh 1)

Ta có $S O ⊥ (A B C D)$ và OM, ON, OP, OQ lần lượt vuông góc với AB, BC, CD, DA

Theo định lí ba đường vuông góc ta có $S M ⊥ A B, S N ⊥ B C, S P ⊥ C D, S Q ⊥ D A$

Từ đó suy ra $\hat{S M O} = \hat{S N O} = \hat{S P O} = \hat{S Q O}$

Xét tam giác SMO vuông tại O ta có $\tan \hat{S M O} = \sqrt{3} \Rightarrow \hat{S M O} = 60^{0}$

Vậy mỗi mặt bên hợp với đáy các góc bằng nhau và bằng 60^o

Câu 35:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, $S A ⊥ (A B C) .$ Gọi E, F lần lượt là trung điểm của các cạnh AB và AC. Góc giữa hai mặt phẳng (SEF) và (SBC) là :

A. $\hat{CSF}$

B. $\hat{BSF}$

C. $\hat{BSE}$

D. $\hat{CSE}$

Xem đáp án

Chọn C

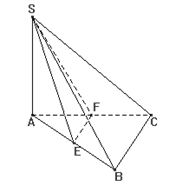
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc mp ABC Gọi E, F lần lượt là trung điểm của các cạnh AB và AC (ảnh 1)

Ta có:

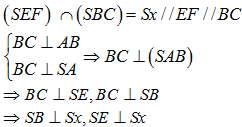
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc mp ABC Gọi E, F lần lượt là trung điểm của các cạnh AB và AC (ảnh 2)

=> Góc giữa hai mặt phẳng (SEF) và (SBC) là : $\hat{BSE}$

Câu 36:

Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B, C lần lượt lấy D, E nằm trên cùng một phía đối với (P) sao cho

B D = a \frac{\sqrt{3}}{2}, C E = a \sqrt{3}

. Góc giữa (P) và (ADE) bằng bao nhiêu?

A. 30^o

B. 60^o

C. 90^o

D. 45^o

Xem đáp án

Chọn B

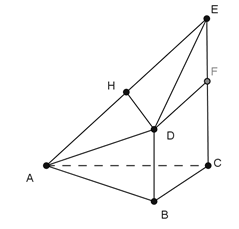
Cho tam giác đều ABC có cạnh bằng a và nằm trong mặt phẳng (P). Trên các đường thẳng vuông góc với (P) tại B, C lần lượt lấy D, E nằm trên cùng một phía đối với (P) sao cho BD = a căn bậc hai 3/2 (ảnh 1)

Gọi $φ = ((A B C), (A D E))$

Ta có: $S_{A B C} = \frac{a^{2} \sqrt{3}}{4}$

Mặt khác, ta có:

$A D = \sqrt{A B^{2} + B D^{2}} = \sqrt{a^{2} + \frac{3 a^{2}}{4}} = \frac{a \sqrt{7}}{2} A E = \sqrt{A C^{2} + C E^{2}} = \sqrt{a^{2} + 3 a^{2}} = 2 a$

Gọi F là trung điểm EC, ta có DF = BC = a

Do đó $D E = \sqrt{D F^{2} + F E^{2}} = \sqrt{a^{2} + \frac{3 a^{2}}{4}} = \frac{a \sqrt{7}}{2}$

Suy ra tam giác ADE cân tại D

Gọi H là trung điểm AE, ta có $D H = \sqrt{A D^{2} - A H^{2}} = \sqrt{\frac{7 a^{2}}{4} - a^{2}} = \frac{a \sqrt{3}}{2}$

Suy ra $S_{A D E} = \frac{1}{2} D H . A E = \frac{1}{2} . \frac{a \sqrt{3}}{2} .2 a = \frac{a^{2} \sqrt{3}}{2}$

Vậy $\cos φ = \frac{S_{A B C}}{S_{A D E}} = \frac{\frac{a^{2} \sqrt{3}}{4}}{\frac{a^{2} \sqrt{3}}{2}} = \frac{1}{2} \Rightarrow φ = 60^{o}$

Câu 37:

Cho góc tam diện Sxyz với

\hat{x S y} = 120^{0}, \hat{y S z} = 60^{0}, \hat{z S x} = 90^{0}

. Trên các tia Sx, Sy, Sz lần lượt lấy các điểm A, B, C sao cho SA = SB = SC = a. Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:

A. 15^o

B. 90^o

C. 45^o

D. 60^o

Xem đáp án

Chọn B

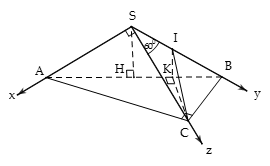
Cho góc tam diện Sxyz với góc xSy = 120 độ, góc ySz = 60 độ, góc zSx = 90 độ. Trên các tia Sx, Sy, Sz lần lượt lấy các điểm (ảnh 1)

Áp dụng định lí Côsin trong tam giác SAB, ta có $A B = a \sqrt{3}$

Tam giác SAC vuông cân tại S nên $A C = a \sqrt{2}$ ; tam giác SBC đều nên BC = a

Vì $A C^{2} + B C^{2} = A B^{2}$ nên tam giác ABCvuông tại C

Gọi H là trung điểm AB thì ta có

$\{\begin{cases} H A = H B = H C \\ S A = S B = S C \end{cases} \Rightarrow S H ⊥ (A B C)$

Mà $S H \subset (S A B)$ nên $(S A B) ⊥ (A B C)$

Vậy $(\hat{(S A B), (A B C)}) = 90^{0}$

Câu 38:

Cho tam giác đều ABC cạnh a. Gọi d_B, d_C lần lượt là đường thẳng đi qua B, C và vuông góc với (ABC). (P) là mặt phẳng qua A và hợp với (ABC) góc 60^o. (P) cắt d_B, d_C lần lượt tại D và E. biết

A D = a \frac{\sqrt{6}}{2}, A E = a \sqrt{3} .

đặt

\hat{D A E} = φ

. Chọn khẳng định đúng trong các khẳng định sau?

A. $\sin φ = \frac{2}{\sqrt{6}}$

B. $φ = 60^{0}$

C. $\sin φ = \frac{3}{\sqrt{6}}$

D. $φ = 30^{0}$

Xem đáp án

Chọn A

Cho tam giác đều ABC cạnh a. Gọi dB, dC lần lượt là đường thẳng đi qua B, C và vuông góc với (ABC). (P) là mặt phẳng qua A và hợp với (ABC) góc 60 độ (ảnh 1)

Ta có: $S_{A B C} = S_{A D E} . \cos α$ với $α = ((A B C), (A D E)) = 60^{0}$

Do đó $S_{A D E} = \frac{S_{A B C}}{\cos α} = \frac{\frac{a^{2} \sqrt{3}}{4}}{\cos 60^{0}} = \frac{a^{2} \sqrt{3}}{2}$

Mặt khác, $S_{A D E} = \frac{1}{2} A D . A E . \sin φ \Leftrightarrow \frac{a^{2} \sqrt{3}}{2} = \frac{1}{2} . \frac{a \sqrt{6}}{2} . a \sqrt{3} . \sin φ \Rightarrow \sin φ = \frac{2}{\sqrt{6}}$

Trắc nghiệm Toán 11 Bài 4: Hai mặt phẳng vuông góc có đáp án (Mới nhất)

Dạng 1: Góc giữa hai mặt phẳng có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương