12 câu hỏi trắc nghiệm thuộc Dạng 4: Các cách tính diện tích tam giác có đáp án

Câu 1:

Cho tam giác ABC có \(a = 4\sqrt 3 \); b = 4 và \(\widehat C = 60^\circ \). Tính diện tích tam giác ABC.

Xem đáp án

Hướng dẫn giải:

Ta áp dụng công thức \(S = \frac{1}{2}ab\sin C\), ta có diện tích tam giác ABC:

\(S = \frac{1}{2}.4\sqrt 3 .4.\sin 60^\circ = 12\).

Câu 2:

Tính diện tích tam giác ABC biết các cạnh a = 4, b = 5, c = 3.

Xem đáp án

Hướng dẫn giải:

Cách 1. Ta có \(p = \frac{1}{2}.\left( {3 + 4 + 5} \right) = 6\).

Áp dụng công thức Heron, ta có:

\(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {6\left( {6 - 4} \right)\left( {6 - 5} \right)\left( {6 - 3} \right)} = 6\).

Cách 2. Nhận thấy \({b^2} = {a^2} + {c^2}\) ( vì \({5^2} = {3^2} + {4^2}\))

Suy ra tam giác ABC vuông tại B, do đó diện tích tam giác ABC là:

\(S = \frac{1}{2}a.c = \frac{1}{2}.3.4 = 6\).

Câu 3:

Cho tam giác ABC có b = 10, c = 15 và \(\widehat A = 30^\circ \). Diện tích tam giác ABC là:

A. \(\frac{{75}}{2}\);

B. \(\frac{{65}}{2}\);

C. \(\frac{{55}}{2}\);

D. \(\frac{{85}}{2}\).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta áp dụng công thức \(S = \frac{1}{2}bc\sin A\), ta có:

\(S = \frac{1}{2}.10.15.\sin 30^\circ = \frac{{75}}{2}\).

Câu 4:

Cho tam giác ABC có AB = 5 , \(\widehat A = 30^\circ \), \(\widehat B = 75^\circ \). Tính diện tích tam giác ABC.

A. \(\frac{5}{2}\);

B. 4;

C. \(\frac{{25}}{4}\);

D. 5.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Trong tam giác ABC có: \(\widehat C = 180^\circ - \left( {\widehat A + \widehat B} \right) = 180^\circ - \left( {30^\circ + 75^\circ } \right) = 75^\circ \).

Suy ra tam giác ABC cân tại A, suy ra AB = AC = 5.

Do đó diện tích tam giác ABC là: \(S = \frac{1}{2}.AB.AC.\sin A = \frac{1}{2}.5.5.\sin 30^\circ = \frac{{25}}{4}\).

Câu 5:

Tam giác ABC có a = 10, b = 21, c = 17. Diện tích tam giác ABC bằng:

A. 24;

B. 84;

C. 42;

D. 48.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là B.

Ta có \(p = \frac{1}{2}\left( {a + b + c} \right) = \frac{1}{2}\left( {10 + 21 + 17} \right) = 24\).

Do đó diện tích tam giác ABC là:

S = \(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \sqrt {24\left( {24 - 10} \right)\left( {24 - 21} \right)\left( {24 - 17} \right)} \)= 84.

Câu 6:

Diện tích của một lá cờ hình tam giác cân (như hình dưới) có độ dài cạnh bên là 80 cm và góc ở đỉnh là 50° gần với giá trị nào nhất?

A. 3 451 cm²;

B. 2 451 cm²;

C. 4 451 cm²;

D. 5 451 cm².

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: Diện tích lá cờ hình tam giác cân là:

S = \(\frac{1}{2}\). 80. 80.sin 50° ≈ 2451,34 (cm²).

Câu 7:

Tam giác đều nội tiếp đường tròn bán kính R = 8 cm có diện tích là:

A. 12\(\sqrt 3 \);

B. 24\(\sqrt 3 \);

C. 48\(\sqrt 3 \);

D. 6\(\sqrt 3 \).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Giả sử tam giác ABC đều nội tiếp đường tròn bán kính R = 8 cm.

Do tam giác ABC đều nên ta có \(\widehat A = 60^\circ \).

Sử dụng công thức định lý sin: \(\frac{a}{{\sin A}} = 2R\)

⇒ a = 2R . sinA = 2 . 8 . sin60° = \(8\sqrt 3 \)

Do tam giác ABC đều nên ta có a = b và \(\widehat C = 60^\circ \), áp dụng công thức \(S = \frac{1}{2}ab\sin C\) ta có diện tích tam giác là S = \(\frac{1}{2}.8\sqrt 3 .8\sqrt 3 .\sin 60^\circ = 48\sqrt 3 \).

Câu 8:

Cho tam giác ABC có a = 5, b = 7, cos C = 0,6. Tính diện tích tam giác ABC.

A. 14;

B. 15;

C. 16;

D. 17.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Theo định lí côsin ta có: \({c^2} = {a^2} + {b^2} - 2ab\cos C = {5^2} + {7^2} - 2.5.7.0,6 = 32\)

Do đó: c = 4\(\sqrt 2 \).

Nửa chu vi tam giác ABC là: p = \(\frac{1}{2}\)(a + b + c) = 6 + 2\(\sqrt 2 \).

Vậy diện tích tam giác ABC là:

S = \(\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)= 14.

Câu 9:

Hình bình hành ABCD có AB = a, BC = 2a và \(\widehat {ABC} = 60^\circ \). Khi đó hình bình hành có diện tích bằng:

A. \(\frac{{{a^2}\sqrt 3 }}{2}\);

B. \({a^2}\sqrt 3 \);

C. \(\frac{{{a^2}\sqrt 3 }}{3}\);

D. \(\frac{{{a^2}\sqrt 3 }}{6}\).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

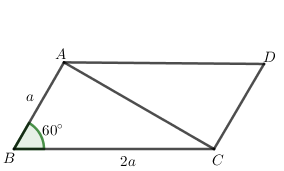
Diện tích tam giác ABC là: S = \(\frac{1}{2}\)AB.AC sinABC = \(\frac{1}{2}.a.2a.\sin 60^\circ \) = \(\frac{{{a^2}\sqrt 3 }}{2}\).

Do đó diện tích hình bình hành ABCD là: \({S_{ABCD}}\)= 2S = \({a^2}\sqrt 3 \).

Câu 10:

Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:

A. 60°;

B. 90°;

C. 120°;

D. 150°.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Diện tích tam giác ABC là: S = \(\frac{1}{2}\)BC.AC sinC = \(\frac{1}{2}\)absinC.

Mà sinC ≥ 1. Nên để tam giác ABC có diện tích lớn nhất thì sinC = 1

\( \Leftrightarrow \widehat C = 90^\circ \).

Câu 11:

Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu cạnh AB tăng lên 3 lần, cạnh AC tăng lên 4 lần và giữ nguyên độ lớn của góc A thì khi đó diện tích của tam giác mới được tạo nên bằng:

A. 7S;

B. 12S;

C. S;

D. 5S.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: Diện tích tam giác ABC là: S = \(\frac{1}{2}\).AB. AC.sinA = \(\frac{1}{2}\).bc.sinA.

Nếu cạnh AB tăng lên 3 lần, cạnh AC tăng lên 4 lần và giữ nguyên độ lớn của góc A thì khi đó diện tích của tam giác mới là:

\({S_1}\)= \(\frac{1}{2}\).3AB. 4AC.sinA = 12.\(\frac{1}{2}\).bc.sinA = 12S.

Câu 12:

Tam giác ABC có AB = \(2\sqrt 2 \), AC = \(2\sqrt 3 \) và độ dài đường cao AH = 2. Khi đó diện tích tam giác ABC bằng:

A. 3 + 3\(\sqrt 3 \);

B. 2 + 3\(\sqrt 2 \);

C. 3 + 2\(\sqrt 2 \);

D. 2 + 2\(\sqrt 2 \).

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

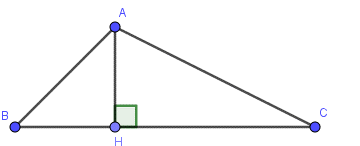
Áp dụng định lý Pythagore ta có:

BH = \(\sqrt {A{B^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {2^2}} = 2\)

Tương tự: CH = \(\sqrt {A{C^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}} = 2\sqrt 2 \).

Do đó BC = BH + CH = 2 + 2\(\sqrt 2 \).

Vậy diện tích tam giác ABC là: S = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\). 2. (2 + 2\(\sqrt 2 \)) = 2 + 2\(\sqrt 2 \).

Trắc nghiệm Toán 10 CTST Bài 2. Định lý côsin và định lý sin có đáp án

Dạng 4: Các cách tính diện tích tam giác có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương