Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án
Dạng 6: Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc có đáp án
-
617 lượt thi
-
12 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Xem đáp án
Hướng dẫn giải:
Chuyển máy tính về chế độ tính “độ” như hướng dẫn ở trên.
Để tính sin130°23'48", ta ấn liên tiếp các phím sau đây:
Và được kết quả sin130°23'48" ≈ 0,7615760123, với kết quả hiện thị màn hình như hình dưới đây.
Để tính cos α, tan α ta cũng làm như trên, chỉ thay phím sin bằng phím cos và tan. Trường hợp muốn tính cotα, ta tính \(\frac{1}{{\tan \alpha }}\).
Câu 2:
Xem đáp án
Hướng dẫn giải:
Để tìm α khi biết cos α = −0,1234, ta ấn liên tiếp các phím sau đây:
Và được kết quả α ≈ 97°5'18", với kết quả hiển thị trên màn hình như hình dưới đây
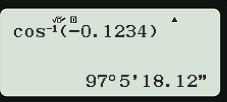
Để tính α biết sinα, tanα ta cũng làm như trên, chỉ thay phím cos bằng phím sin và tan. Khi biết cotα, ta suy ra tanα rồi tính góc.
Câu 3:
Tính cos123°48'53" (làm tròn đến hàng phần trăm).
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Để tính cos123°48'53", ta ấn liên tiếp các phím sau đây:
Và được kết quả cos123°48'53" ≈ – 0,5565091196 ≈ – 0,56, với kết quả hiện thị màn hình như hình dưới đây.
Câu 4:
Tìm α (0° ≤ α < 90°) biết sin α = 0,4893.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Để tìm α khi biết sin α = 0,4893, ta ấn liên tiếp các phím sau đây:
Và được kết quả α ≈ 29°17'40", với kết quả hiển thị trên màn hình như hình dưới đây
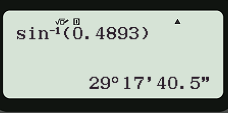
Câu 5:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Để tính tan148°14'63", ta ấn liên tiếp các phím sau đây:
Và được kết quả tan148°14'63" ≈ – 0,6187986629 ≈ – 0,62, với kết quả hiện thị màn hình như hình dưới đây.
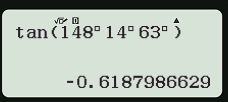
Câu 6:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Để tìm α khi biết tan α = 1,587, ta ấn liên tiếp các phím sau đây:
Và được kết quả α ≈ 57°47'3", với hiển thị trên màn hình như hình dưới đây
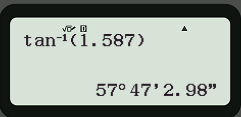
Câu 7:
Cho α = 23°56'. Giá trị của cot α gần nhất với giá trị nào sau đây?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Để tính cot α , đầu tiên ta tính tan α với α = 23°56' bằng cách ta ấn liên tiếp các phím sau đây
Và được kết quả tan23°56' ≈ 0,4438352043, với kết quả hiện thị màn hình như hình dưới đây.
Lại có \(\cot \alpha = \frac{1}{{\tan \alpha }}\), ta tiếp tục bấm liên tiếp các phím sau 1 / Ans .
Và thu được kết quả trên màn hình
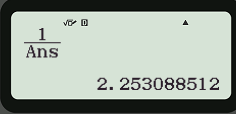
Vậy cotα ≈ 2,253.
Câu 8:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
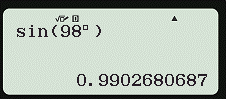
Để tính sin98°, ta ấn liên tiếp các phím sau đây:
Và được kết quả sin98° ≈ 0,9902680687 ≈ 0,99, với kết quả hiện thị màn hình như hình dưới đây.
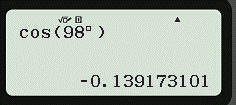
Để tính cos98°, ta ấn liên tiếp các phím sau đây:
Và được kết quả cos98° ≈ − 0,139173101 ≈ − 0,14, với kết quả hiện thị màn hình như hình dưới đây.
Do đó \(\tan 98^\circ = \frac{{\sin 98^\circ }}{{\cos 98^\circ }} \approx \frac{{0,99}}{{ - 0,14}} \approx - 7,07\).
Và \(\cot 98^\circ = \frac{1}{{\tan 98^\circ }} \approx \frac{1}{{ - 7,07}} \approx - 0,14\).
Câu 9:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
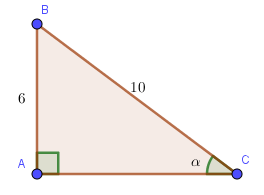
Trong tam giác ABC vuông tại A ta có sin α = \(\frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\).
Để tìm α khi biết sin α = \(\frac{3}{5}\), ta ấn liên tiếp các phím sau đây:
Và được kết quả α ≈ 36°52', với kết quả hiển thị trên màn hình như hình dưới đây
Câu 10:
Tìm tất cả giá trị của α (0° ≤ α ≤ 180°) thỏa mãn sin α = \(\frac{4}{{11}}\).
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Để tìm α khi biết sin α = \(\frac{4}{{11}}\), ta ấn liên tiếp các phím sau đây:
Và được kết quả α ≈ 21,324°, với kết quả hiển thị trên màn hình như hình dưới đây:
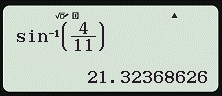
Mặt khác vì 0° ≤ α ≤ 180° mà sin α = sin(180° − α)
Vậy α ≈ 21,324° hoặc α = 180° – 21,324° ≈ 158,676°.
Câu 11:
Cho α (0° ≤ α ≤ 180°) thỏa mãn cot α = 7,486. Giá trị của α gần nhất với:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có: tan α . cot α = 1 \( \Rightarrow \tan \alpha = \frac{1}{{\cot \alpha }} = \frac{1}{{7,486}}\).
Để tìm α ta ấn liên tiếp các phím sau đây:
Vậy ta được kết quả là α ≈ 7°36'31".
Câu 12:
Tam giác DEF có số đo như hình vẽ dưới đây.
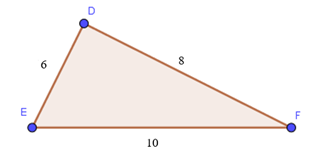
Số đo của góc DEF gần nhất với giá trị:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có: DE2 + DF2 = 62 + 82 = 100; EF2 = 102 = 100.
Suy ra DE2 + DF2 = EF2.
Do đó tam giác DEF vuông tại D (theo định lí Pythagore đảo).
Khi đó ta có: cosDEF = \(\frac{{DE}}{{EF}} = \frac{6}{{10}} = \frac{3}{5}\).
Ấn máy tính, ta tính được \[\widehat {DEF} \approx 53^\circ \].