Trắc nghiệm Toán 10 CTST Bài 1. Giá trị lượng giác của một góc từ 0° đến 180° có đáp án
Dạng 1: Xác định giá trị lượng giác của góc đặc biệt có đáp án
-
798 lượt thi
-
13 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Lấy điểm M trên nửa đường tròn đơn vị sao cho ^xOM=120∘.
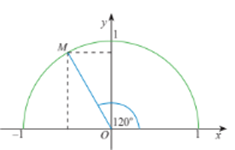 Ta có: ^MOy=120∘−90∘=30∘.
Ta có: ^MOy=120∘−90∘=30∘.
Ta tính được tọa độ điểm M: {x0=−(OM.sin30∘)=−(1.12)=−12y0=OM.cos30∘=1.√32=√32.
Hay M(−12;√32).
Vậy theo định nghĩa ta có:
sin120∘=√32;cos120∘=−12; tan120∘=−√3;cot120∘=−√33.
Câu 2:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có sin135° = sin(180° – 45°) = sin45° = √22;
cos135° = cos(180° – 45°) = – cos45° = −√22;
tan135∘=sin135∘cos135∘=√22−√22=−1.
Do đó cot135° = cos135∘sin135∘=−√22√22=−1.
Câu 3:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Ta có ˆF=180∘−(ˆD+ˆE)=180∘−30∘=150∘.
Do đó sinF = sin150° = sin(180° − 30°) = sin30° = 12;
cosF = cos150° = cos(180° − 30°)= − cos30° = −√32;
tanF = sin150∘cos150∘=12−√32=−√33;
cotF = cos150∘sin150∘=−√3212= −√3.
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có sin120° = sin(180° – 60°) = sin60°=√32.
cos120° = cos(180° – 60° ) = – cos60° =−12.
Do đó tan120∘=sin120∘cos120∘=−√3;
cot120∘=−1√3.
Câu 5:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có sin60° = √32; cos60° = 12; tan60° =√3; cot60° =1√3.
Câu 6:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: tan135° = – tan(180° – 45°) = – 1.
Câu 7:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có:
sin 0° = 0;
cos 90° = 0;
cos 0° = 1;
sin 90° = 1 nên đáp án D sai.
Câu 8:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Ta có sin A = sin 45° = √22, suy ra đáp án sai là A.
cos A = cos 45° = √22;
tan A = tan 45° = 1;
cot A = cot 45° = 1.
Vậy các đáp án B, C, D đúng.
Câu 9:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Ta có sin (180° – α) = sin α = 12.
Do đó ab=12, mà ab là phân số tối giản nên a = 1, b = 2.
Vậy a + b = 1 + 2 = 3.
Câu 10:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có ˆB=60∘ nên sin B = sin 60° = √32; cos B = cos 60° = 12 nên A, B sai.
Lại có ˆC=180∘−(ˆA+ˆB)=180∘−(90∘+60∘)=30∘ (áp dụng định lí tổng ba góc trong tam giác).
Do đó sin C = sin 30° = 12; cos C = cos 30° = √32.
Vậy C đúng, D sai.
Câu 11:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Vì tam giác ABC cân tại A nên ˆB=ˆC=180∘−ˆA2=180∘−120∘2=30∘.
Do đó sinB=sin30∘=12.
Câu 12:
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: cos90° = 0 nên A = 0.
Câu 13:
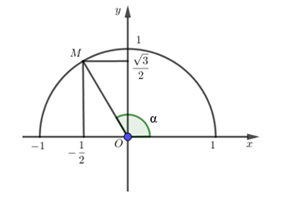
Cho góc α như hình vẽ, xác định giá trị của tan α.
 Xem đáp án
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D.
Từ hình vẽ ta thấy điểm M có tọa độ (−12;√32).
Do đó: tanα=√32−12=−√3.
