10 câu hỏi trắc nghiệm thuộc Dạng 5. Ứng dụng ba đường conic vào các bài toán thực tế

Câu 1:

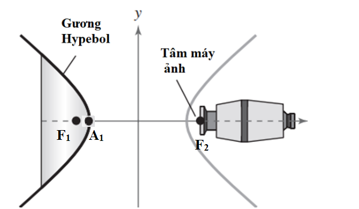
Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang học của máy ảnh được đặt tại một tiêu điểm của gương (hình vẽ).

Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang (ảnh 1)

Phương trình cho mặt cắt của gương là $\frac{x^{2}}{25} - \frac{y^{2}}{16} = 1$ .

Khoảng cách từ quang tâm của máy ảnh đến đỉnh của gương (làm tròn kết quả đến chữ số thập phân thứ nhất) là

A. 12,8;

B. 5;

C. 1,4;

D. 11,4.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Để chụp toàn cảnh, ta có thể sử dụng một gương hypebol. Máy ảnh được hướng về phía đỉnh của gương và tâm quang (ảnh 2)

Gọi $(H) : \frac{x^{2}}{25} - \frac{y^{2}}{16} = 1$ có a² = 25 và b² = 16.

Suy ra $c = \sqrt{a^{2} + b^{2}} = \sqrt{25 + 16} = \sqrt{41}$ .

Ta tìm được một tiêu điểm của gương là $F_{2} (\sqrt{41}; 0)$ và đỉnh của gương là A₁(–5; 0).

Vậy khoảng cách từ tâm của máy ảnh tới đỉnh của gương là $F_{2} A_{1} = \sqrt{41} + 5 \approx 11, 4.$

Câu 2:

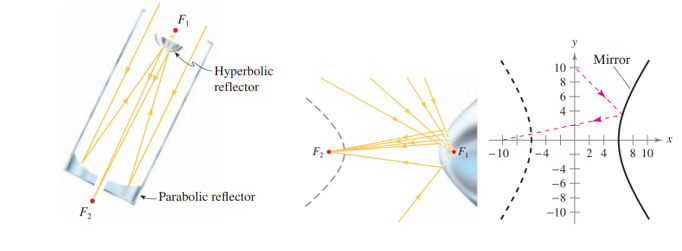
Một gương hypebol (được sử dụng trong một số kính thiên văn) có tính chất là một tia sáng hướng vào tiêu điểm sẽ bị phản xạ sang tiêu điểm khác. Gương trong hình vẽ có phương trình $\frac{x^{2}}{36} - \frac{y^{2}}{64} = 1$ . Điểm nào trên gương sẽ nhận được tia sáng đi qua điểm (0; 10) và bị phản xạ sang tiêu điểm còn lại? (tham khảo hình vẽ)

Một gương hypebol (được sử dụng trong một số kính thiên văn) có tính chất là một tia sáng hướng vào tiêu (ảnh 1)

A. M(6,54; 3,65);

B. M(6,54; 3,55);

C. M(– 32,25; 42,25);

D. M(6,54; – 3,55);.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Gọi $(H) : \frac{x^{2}}{36} - \frac{y^{2}}{64} = 1$

Phương trình của gương (H) có dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ , với a = 6, b = 8;

Suy ra $c = \sqrt{a^{2} + b^{2}} = 10$ .

Giả sử điểm cần tìm là M ∈ (H).

Gọi đường đi của ánh sáng qua điểm (0; 10) và M là d, do tia sáng sau khi phản xạ bởi gương sẽ đi qua tiêu điểm F₁(–10; 0), suy ra d nhằm vào tiêu điểm F₂(10; 0) (F₂ ∈ d).

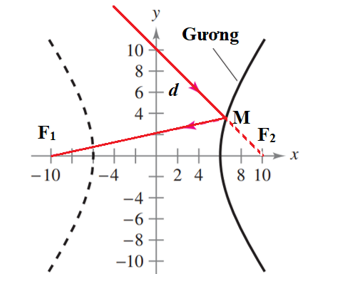
Một gương hypebol (được sử dụng trong một số kính thiên văn) có tính chất là một tia sáng hướng vào tiêu (ảnh 2)

Từ đây dễ dàng lập được phương trình của d là y = –x + 10.

Tọa độ của M ∈ (H) là nghiệm của hệ: $\{\begin{cases} y = - x + 10 \\ \frac{x^{2}}{36} - \frac{y^{2}}{64} = 1 \end{cases} \Leftrightarrow \{\begin{cases} y = - x + 10 \\ 16 x^{2} - 9 y^{2} - 576 = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} y = - x + 10 \\ 16 x^{2} - 9 {(10 - x)}^{2} - 576 = 0 \end{cases} \Leftrightarrow \{\begin{cases} y = - x + 10 \\ 16 x^{2} - 9 (100 - 20 x + x^{2}) - 576 = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} y = - x + 10 \\ 7 x^{2} + 180 x - 1 476 = 0 \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x \approx - 32, 25 \\ y \approx 42, 25 \end{cases} \\ \{\begin{cases} x \approx 6, 54 \\ y \approx 3, 46 \end{cases} \end{array}$

Do điểm cần tìm nằm ở nhánh bên phải nên ta có M(6,54; 3,55).

Câu 3:

Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được truyền bởi hai trạm phát đặt cách xa nhau. Các xung này di chuyển với tốc độ ánh sáng (186 000 dặm/giây). Sự chênh lệch về thời gian nhận được phản xạ của các xung này từ một máy bay hoặc tàu thủy là không đổi, nên máy bay hoặc con tàu sẽ nằm trên một hyperbol có các trạm phát là các tiêu điểm. Giả sử rằng hai trạm phát cách nhau 300 dặm, được đặt trên một hệ tọa độ vuông góc tại các điểm có tọa độ (–150; 0) và (150; 0) và một con tàu đang đi trên một con đường là một nhánh của hypebol và có tọa độ (x; 75) (xem hình vẽ).

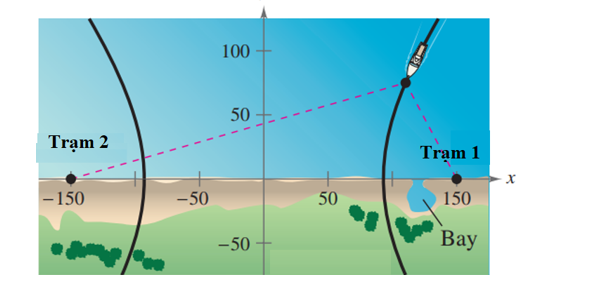
Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được (ảnh 1)

Giá trị gần đúng của hoành độ của vị trí con tàu khi chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây) là

A. 110,2789;

B. –110,2789;

C. 52,3891;

D. 73,4231.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Gọi đường đi của con tàu là (H) thì (H) có phương trình dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (a, b > 0).

Với giả thiết ta có các tiêu điểm của (H) là F₁(–150; 0) và F₂(150; 0), suy ra c = 150.

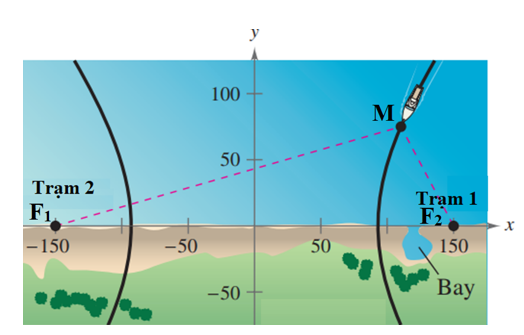
Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được (ảnh 2)

Giả sử vị trí con tàu hiện tại là M(x₀; 75) ∈ (H); theo giả thiết độ chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây), tức là ta có |MF₁ – MF₂| = 0,001.186 000 = 186 (dặm); tức là ta có 2a = 186 suy ra a = 93.

Do đó $b = \sqrt{c^{2} - a^{2}} = 27 \sqrt{19} .$

Phương trình (H) là: $\frac{x^{2}}{8 649} - \frac{y^{2}}{13 851} = 1$ .

Ta có M(x₀; 75) ∈ (H) $\Leftrightarrow \frac{x^{2}}{8 649} - \frac{75^{2}}{13 851} = 1 \Leftrightarrow [\begin{array}{l} x \approx 110, 2789 \\ x \approx - 110, 2789 \end{array}$ .

Vậy hoành độ của con tàu gần bằng 110,2789.

Câu 4:

Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ được truyền bởi các trạm phát đặt cách xa nhau. Các xung này di chuyển với tốc độ ánh sáng (186 000 dặm/giây). Sự chênh lệch về thời gian nhận được phản xạ của các xung này từ một máy bay hoặc tàu thủy là không đổi, nên máy bay hoặc con tàu sẽ nằm trên một hyperbol có các trạm phát là các tiêu điểm. Giả sử rằng hai trạm phát, cách nhau 300 dặm, được đặt trên một hệ tọa độ vuông góc tại các điểm có tọa độ (–150; 0) và (150; 0) và một con tàu đang đi trên một con đường là một nhánh của hypebol (xem hình vẽ).

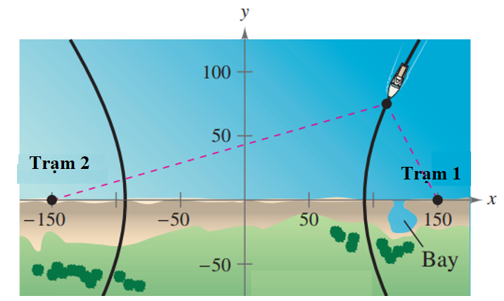
Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ (ảnh 1)

Biết rằng độ chênh lệch thời gian giữa các xung từ các trạm phát với con tàu là 1 000 micro giây (0,001 giây). Khoảng cách giữa tàu và trạm phát số 1 khi tàu vào bờ là

A. 93;

B. 57;

C. 150;

D. 243.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

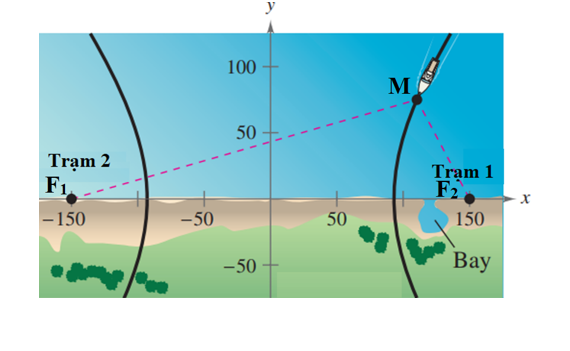
Điều hướng LORAN (điều hướng vô tuyến đường dài) cho máy bay và tàu thủy sử dụng các xung đồng bộ (ảnh 2)

Gọi đường đi của con tàu là (H) thì (H) có phương trình dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ (a, b > 0).

Với giả thiết ta có các tiêu điểm của (H) là F₁(–150; 0) và F₂(150; 0), suy ra c = 150.

Giả sử vị trí con tàu hiện tại là M(x₀; 75) ∈ (H); theo giả thiết độ chênh lệch thời gian giữa các xung từ các trạm phát là 1 000 micro giây (0,001 giây), tức là ta có |MF₁ – MF₂| = 0,001.186 000 = 186 (dặm); tức là ta có 2a = 186 suy ra a = 93.

Do đó $b = \sqrt{c^{2} - a^{2}} = 27 \sqrt{19} .$

Phương trình (H) là: $\frac{x^{2}}{8 649} - \frac{y^{2}}{13 851} = 1$ .

Trạm phát số 1 nằm tại tiêu điểm F₂(150; 0), vị trí khi con tàu vào bờ là đỉnh của (H) là A₂(93; 0).

Vậy khoảng cách từ vị trí tàu vào bờ đến trạm số 1 là: F₂A₂ = 150 – 93 = 57 (dặm).

Câu 5:

Một con tàu đang trên hành trình đi song song với một bờ biển thẳng và cách bờ 80 km. Hai trạm truyền tin S₁ và S₂ nằm trên bờ biển, cách xa nhau 220 km. Bằng cách tính giờ các tín hiệu vô tuyến từ hai trạm, hoa tiêu của tàu xác định rằng con tàu đang ở giữa hai trạm và ở gần S₂ hơn S₁ là 60 km. Khoảng cách từ con tàu tới trạm S₂ (làm tròn đến hai chữ số thập phân) là

A. 107,89 km;

B. 167,89 km;

C. 136,01 km;

D. 75,50 km.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Gọi d₁ và d₂ là các khoảng cách tương ứng từ con tàu tới S₁ và S₂, khi đó hiệu d₁ – d₂ = 60 và con thuyền phải nằm trên một hyperbol với tiêu điểm là S₁ và S₂, hiệu hai khoảng cách cố định bằng 60 (Hình vẽ).

Để đưa ra phương trình của hyperbol, ta biểu diễn hiệu cố định này bằng 2a.

Như vậy, ta có c = 110, $a = \frac{1}{2} \cdot 60 = 30, b = \sqrt{110^{2} - 30^{2}} = \sqrt{11 200}$

Phương trình của hyperbol này có dạng là $\frac{x^{2}}{900} - \frac{y^{2}}{11 200} = 1$ .

Thay y = 80 vào phương trình và giải theo x ta được:

$\frac{x^{2}}{900} - \frac{80^{2}}{11 200} = 1 \Leftrightarrow x^{2} = \frac{9 900}{7}$

Do đó x ≈ 37,61 (nghiệm âm bị loại, vì con tàu ở gần S₂ hơn S₁).

Khoảng cách từ con tàu đến S₂ là $d_{2} \approx \sqrt{{(37, 61 - 110)}^{2} + 80^{2}} = \sqrt{11640, 3121} \approx 107, 89$ km.

Câu 6:

Một vụ nổ được hai micro M₁ và M₂ cách nhau 2 dặm ghi lại (1 dặm bằng 5 280 feet). Micro M₁ nhận được âm thanh trước 4 giây so với micro M₂. Giả sử âm thanh di chuyển với tốc độ 1 100 feet/giây. Tập tất cả các điểm P xảy ra vụ nổ thỏa mãn các điều kiện trên là một hypebol có phương trình dạng $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ , với hai micro M₁ và M₂ là các tiêu điểm. Khi đó a + b bằng bao nhiêu? (làm tròn đến chữ số hàng đơn vị)

A. 2 200;

B. 4 800;

C. 5 280;

D. 7 000.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Ta bắt đầu bằng cách đặt micro trong một hệ tọa độ vuông góc. Bởi vì dặm bằng 5 280 feet nên ta đặt M₁ trên trục hoành cách gốc tọa độ 5280 feet về bên phải và đặt M₂ trên trục hoành cách gốc tọa độ 5 280 feet về bên trái như hình vẽ minh họa hai micro cách nhau 2 dặm.

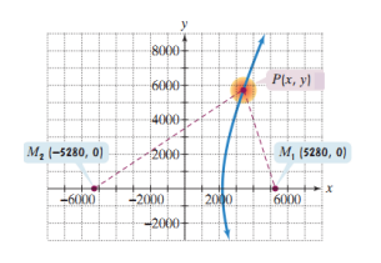
Một vụ nổ được hai micro M1 và M2 cách nhau 2 dặm ghi lại ( dặm bằng 5 280 feet). Micro M1 nhận được (ảnh 1)

Ta biết rằng M₂ nhận được âm thanh sau 4 giây so với M₁. Vì âm thanh di chuyển với tốc độ 1 100 feet/giây nên hiệu số khoảng cách từ P (nơi xảy ra vụ nổ) tới M₂ và từ P tới M₁ là 4 400 feet.

Tập tất cả các điểm P xảy ra vụ nổ thỏa mãn các điều kiện này là một hyperbol, với hai micro M₁ và M₂ là các tiêu điểm.

Như vậy, vị trí xảy ra vụ nổ nằm trên hyperbol có phương trình chuẩn là $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ .

Ta cần xác định các hệ số a và b.

Ta có hiệu số khoảng cách giữa hai micro là 4 400 feet và được đặt bằng 2a, tức là 2a = 4 400 suy ra a = 2 200.

Ta có $\frac{x^{2}}{2 200^{2}} - \frac{y^{2}}{b^{2}} = 1$ hay $\frac{x^{2}}{4 840 000} - \frac{y^{2}}{b^{2}} = 1$ .

Ta lại có khoảng cách từ gốc O(0; 0) tới tiêu điểm M₂(–5 280; 0) hoặc M₁(5 280; 0) đều bằng 5 280. Do đó c = 5 280.

Sử dụng hệ thức $c^{2} = a^{2} + b^{2} \Rightarrow b = \sqrt{5 280^{2} - 2 200^{2}} \approx 4 800.$

Vậy a + b = 2 200 + 4 800 = 7 000.

Câu 7:

Hai tháp vô tuyến cách nhau 200 km được đặt dọc bờ biển với A nằm về phía Tây đối với B. Các tín hiệu vô tuyến được gửi đồng thời từ mỗi tháp tới một con tàu và tín hiệu ở B nhận được sớm hơn 500 micro giây trước tín hiệu ở A. Giả sử rằng các tín hiệu vô tuyến truyền đi với vận tốc 300 mét/micro giây và con tàu nằm về phía Bắc của tháp B thì tàu cách bờ biển bao xa (làm tròn đến hai chữ số thập phân)?

A. 75,00 km;

B. 66,14 km;

C. 100,00 km;

D. 58,33 km.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Theo đề bài con tàu nhận được tín hiệu từ B sớm hơn từ A 500 micro giây,

Vì âm thanh di chuyển với tốc độ 300 mét/micro giây nên hiệu số khoảng cách từ con tàu tới A và B là 500 . 300 m = 150 000m = 150 km.

Hiệu khoảng cách này là 2a = 150 suy ra a = 75.

Con tàu nằm trên một nhánh của hyperbol, với hai tháp vô tuyến A và B là hai tiêu điểm, A và B cách nhau 200 km, nghĩa là 2c = 200 suy ra c = 100.

Theo tính chất của hyperbol, $b = \sqrt{c^{2} - a^{2}} = \sqrt{100^{2} - 75^{2}} = \sqrt{4 375},$ và phương trình chuẩn của hyperbol là $\frac{x^{2}}{5 625} - \frac{y^{2}}{4 375} = 1$ .

Vì con tàu nằm về phía Bắc của tháp B, nghĩa là có hoành độ x = c = 100.

Thay x = 100 vào phương trình trên ta có y ≈ 58,33.

Vậy tàu cách bờ biển khoảng 58,33 km.

Câu 8:

Một kiến trúc sư quan tâm đến việc thiết kế một mái vòm mỏng có hình dạng của hình Hyperbolic parabolid như Hình 1. Hỏi điểm thuộc Hyperbol nằm cao hơn đỉnh 6 m ở bên phải cách đỉnh bao xa (làm tròn tới hai chữ số thập phân)?

Một kiến trúc sư quan tâm đến việc thiết kế một mái vòm mỏng có hình dạng của hình Hyperbolic parabolid như Hình 1. (ảnh 1)

A. 6,48 m;

B. 3,16 m;

C. 10,31 m;

D. 8,83 m.

Xem đáp án

Một kiến trúc sư quan tâm đến việc thiết kế một mái vòm mỏng có hình dạng của hình Hyperbolic parabolid như Hình 1. (ảnh 2)

Câu 9:

Một tòa tháp có mặt cắt hình hypebol có phương trình $\frac{x^{2}}{36} - \frac{y^{2}}{49} = 1$ . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng

A. 43,28 m;

B. 22,25 m;

C. 28,31 m;

D. 57,91 m.

Xem đáp án

Một tòa tháp có mặt cắt hình hypebol có phương trình x^2 / 36 - y^2 / 49=1 . Biết khoảng cách từ nóc tháp đến tâm đối (ảnh 1)

Câu 10:

Một anten gương đơn hình parabol có phương trình y² = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là

A. (0; 10);

B. (0 ; 5);

C. (10; 0);

D. (5; 0).

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Phương trình parabol có dạng y² = 2px, với p = 10.

Suy ra $\frac{p}{2} = \frac{10}{2} = 5$ .

Khi đó tọa độ tiêu điểm F(5; 0).

Vậy ta sẽ đặt ống thu tại điểm có tọa độ (5; 0).

Do đó ta chọn phương án D.

Trắc nghiệm Toán 10 Bài 22. Ba đường conic có đáp án

Dạng 5. Ứng dụng ba đường conic vào các bài toán thực tế

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương