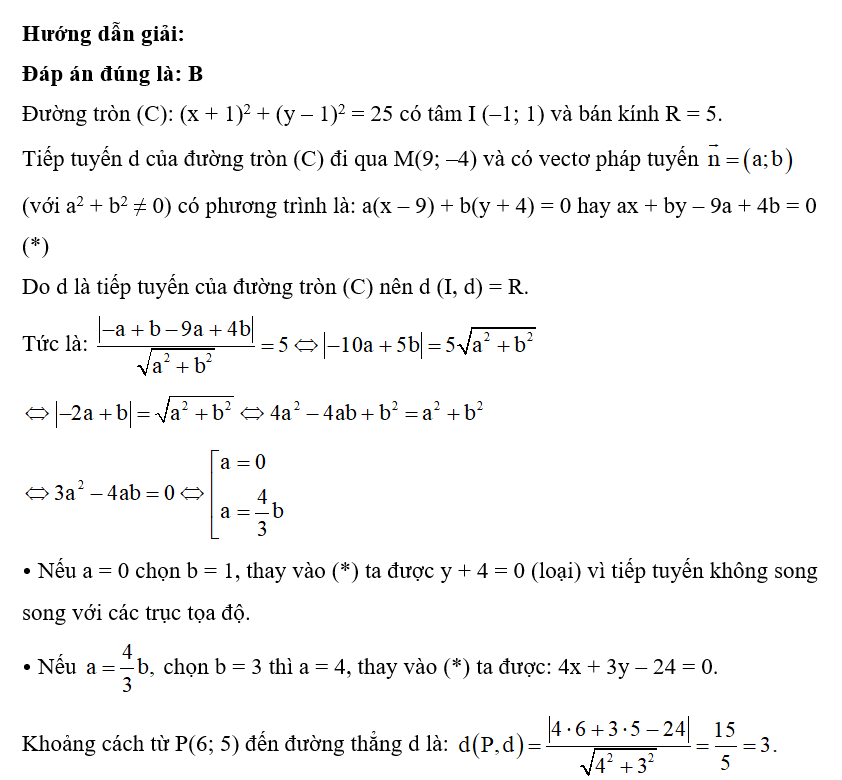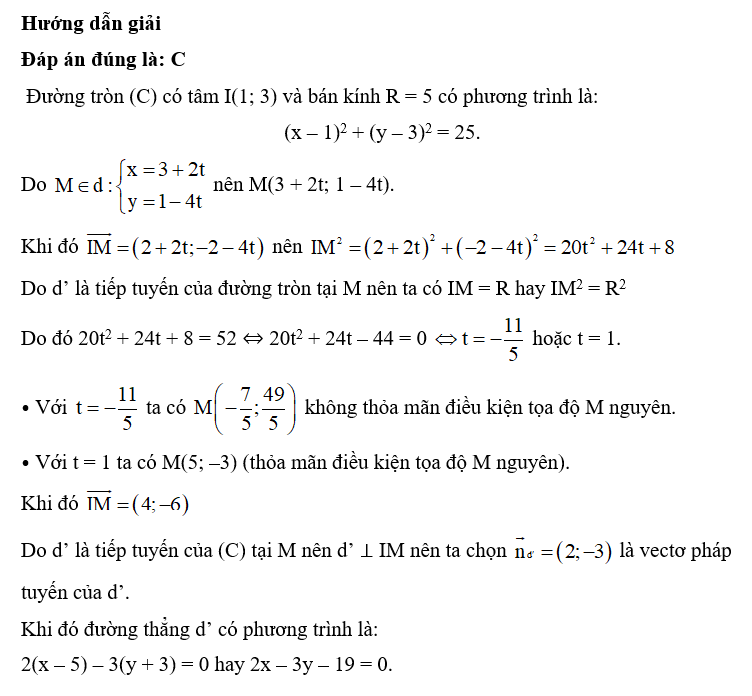10 câu hỏi trắc nghiệm thuộc Dạng 3. Phương trình tiếp tuyến của đường tròn

Câu 1:

Trong mặt phẳng tọa độ Oxy, đường tròn x² + y² – 1 = 0 tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?

A. 3x – 4y + 5 = 0;

B. x + y = 0;

C. 3x + 4y – 1 = 0;

D. x + y – 1 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A

Đường tròn có tâm O(0; 0) bán kính R = 1.

Điều kiện để đường thẳng tiếp xúc với đường tròn là khoảng cách từ tâm tới đường thẳng bằng bán kính.

Xét phương án A: đường thẳng ∆: 3x – 4y + 5 = 0.

$d (O, Δ) = \frac{|3 \cdot 0 - 4 \cdot 0 + 5|}{\sqrt{3^{2} + 4^{2}}} = \frac{5}{5} = 1 = R .$

Do đó đường thẳng 3x – 4y + 5 = 0 tiếp xúc với đường tròn.

Câu 2:

Trong mặt phẳng tọa độ Oxy, đường tròn nào sau đây tiếp xúc với trục Ox?

A. x² + y² – 10x = 0;

B. x² + y² – 5 = 0;

C. x² + y² – 10x – 2y + 1 = 0;

D. x² + y² + 6x + 5y + 9 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Đường tròn (C) tiếp xúc với trục Ox khi d(I, Ox) = R với I và R lần lượt là tâm và bán kính của đường tròn (C).

Xét phương trình đường tròn: x² + y² + 6x + 5y + 9 = 0 có $I (- 3; - \frac{5}{2})$ và $R = \frac{5}{2}$ .

d(I, Ox) = $\frac{5}{2} = R$ . Vậy (C) tiếp xúc với trục Ox.

Câu 3:

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + y² – 2x – 4y + 3 = 0. Tiếp tuyến của đường tròn (C) song song với đường thẳng Δ: 3x + 4y + 1 = 0 có phương trình là

A. $3 x + 4 y + 5 \sqrt{2} - 11 = 0$ và $3 x + 4 y - 5 \sqrt{2} + 11 = 0$ ;

B. $3 x + 4 y + 5 \sqrt{2} - 11 = 0$ và $3 x + 4 y - 5 \sqrt{2} - 11 = 0$ ;

C. $3 x + 4 y + 5 \sqrt{2} - 11 = 0$ và $3 x + 4 y + 5 \sqrt{2} + 11 = 0$ ;

D.

3 x + 4 y - 5 \sqrt{2} + 11 = 0

và

3 x + 4 y - 5 \sqrt{2} - 11 = 0

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Đường tròn (C): x² + y² – 2x – 4y + 3 = 0 có tâm I(1; 2) và bán kính $R = \sqrt{2}$ .

Do d song song với đường thẳng Δ nên d có phương trình là 3x + 4y + k = 0 (k ≠ 1).

Để đường thẳng d tiếp xúc với đường tròn (C) thì d(I, d) = R

$\Leftrightarrow \frac{|3 \cdot 1 + 4 \cdot 2 + k|}{\sqrt{3^{2} + 4^{2}}} = \sqrt{2} \Leftrightarrow |11 + k| = 5 \sqrt{2} \Leftrightarrow [\begin{array}{l} 11 + k = 5 \sqrt{2} \\ 11 + k = - 5 \sqrt{2} \end{array} \Leftrightarrow [\begin{array}{l} k = 5 \sqrt{2} - 11 \\ k = - 5 \sqrt{2} - 11 \end{array}$

Vậy có hai phương trình tiếp tuyến cần tìm là $3 x + 4 y + 5 \sqrt{2} - 11 = 0$ và $3 x + 4 y - 5 \sqrt{2} - 11 = 0$ .

Câu 4:

Trong mặt phẳng tọa độ Oxy, phương trình tiếp tuyến của đường tròn (C): (x – 2)² + ( y + 4)² = 25 vuông góc với đường thẳng 3x – 4y + 5 = 0 là

A. 4x + 3y + 29 = 0;

B. 4x + 3y + 29 = 0 và 4x + 3y – 21 = 0;

C. 4x – 3y + 5 = 0 và 4x – 3y – 45 = 0;

D. 4x + 3y + 5 = 0 và 4x + 3y + 3 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B

Đường tròn (C): (x – 2)² + (y + 4)² = 25 có tâm I(2; –4), bán kính R = 5.

Đường thẳng vuông góc với đường thẳng d: 3x – 4y + 5 = 0 có phương trình dạng: 4x + 3y + c = 0.

Đường thẳng Δ là tiếp tuyến của đường tròn (C) khi và chỉ khi d(I, Δ) = R tức là

$\frac{|4.2 + 3. (- 4) + c|}{\sqrt{4^{2} + 3^{2}}} = 5 \Leftrightarrow |c - 4| = 25 \Leftrightarrow [\begin{array}{l} c - 4 = 25 \\ c - 4 = - 25 \end{array} \Leftrightarrow [\begin{array}{l} c = 29 \\ c = - 21 \end{array}$ .

Vậy có hai tiếp tuyến cần tìm là: 4x + 3y + 29 = 0 và 4x + 3y – 21 = 0.

Câu 5:

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)² + (y – 4)² = 36 và điểm P(–3; –2) nằm ngoài đường tròn. Từ điểm P kẻ các tiếp tuyến PM và PN tới đường tròn (C), với M, N là các tiếp điểm. Phương trình đường thẳng MN là

A. x + y + 1 = 0;

B. x – y – 1 = 0;

C. x – y + 1 = 0;

D. x + y – 1 = 0.

Xem đáp án

Hướng dẫn giải :

Đáp án đúng là : D

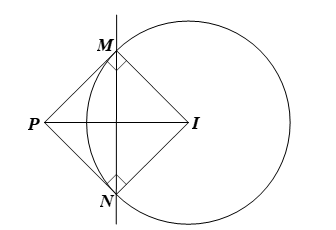
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 36 và điểm P(–3; –2) nằm ngoài đường tròn. (ảnh 1)

Đường tròn (C): (x – 3)² + (y – 4)² = 36 tâm I(3; 4) và bán kính R = 6.

Với P(–3; –2) và I(3; 4) ta có $\vec{P I} = (6; 6)$ nên ta có $P I = \sqrt{6^{2} + 6^{2}} = 6 \sqrt{2} .$

Xét ∆PIM vuông tại M, theo định lí Pythagore ta có :

$P M = \sqrt{P I^{2} - M I^{2}} = \sqrt{{(6 \sqrt{2})}^{2} - 6^{2}} = 6.$

Do đó ∆PIM vuông cân tại M, suy ra tứ giác IMPN là hình vuông nên đường thẳng MN nhận $\vec{n} = \frac{1}{6} \vec{P I} = (1; 1)$ làm vectơ pháp tuyến đồng thời đường thẳng MN đi qua trung điểm K(0; 1) của IP.

Vậy phương trình đường thẳng MN là : 1(x – 0) + 1. ( y – 1) = 0 hay x + y – 1 = 0.

Câu 6:

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình: x² + y² – 4x + 8y + 18 = 0. Phương trình tiếp tuyến của đường tròn (C) đi qua A(1; –3) là

A. x + y + 4 = 0;

B. x + y – 4 = 0;

C. x – y + 4 = 0;

D. x – y – 4 = 0.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D

Đường tròn (C) có tâm I(2; – 4) và bán kính $R = \sqrt{2}$

Thay tọa độ điểm A vào phương trình đường tròn ta thấy điểm A thuộc đường tròn (C). Do đó tiếp tuyến của đường tròn (C) đi qua A chính là tiếp tuyến tại A của đường tròn (C).

Với A(1; –3) và I(2; – 4) ta có $\vec{A I} = (1; - 1) .$ Khi đó tiếp tuyến tại A nhận $\vec{A I} = (1; - 1) .$ làm vectơ pháp tuyến.

Phương trình tiếp tuyến của (C) đi qua A(1; –3) là:

1(x – 1) – 1(y + 3) = 0 hay x – y – 4 = 0.

Câu 7:

Cho đường tròn (C): (x + 1)² + (y – 1)² = 25 và điểm M(9; –4). Gọi d là tiếp tuyến của (C), biết d đi qua M và không song song với các trục tọa độ. Khoảng cách từ điểm P(6; 5) đến d bằng

A. 2;

B. 3;

C. 4;

D. 5.

Xem đáp án

Cho đường tròn (C): (x + 1)2 + (y – 1)2 = 25 và điểm M(9; –4). Gọi d là tiếp tuyến của (C), biết d đi qua M (ảnh 1)

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + y² – 6x + 2y + 5 = 0 và đường thẳng d: 2x + (m – 2) y – m – 7 = 0. Tổng các giá trị của m sao cho đường thẳng d là tiếp tuyến của đường tròn (C) là

A. 10;

B. –10;

C. 16;

D. –16.

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 6x + 2y + 5 = 0 và đường thẳng (ảnh 1)

Câu 9:

Trong mặt phẳng tọa độ Oxy, cho điểm M(–3; 1) và đường tròn (C): x² + y² – 2x – 6y + 6 = 0. Gọi T₁, T₂ là các tiếp điểm của các tiếp tuyến kẻ từ M đến (C). Khoảng cách từ O đến đường thẳng T₁T₂ là

A. 5;

B. $\sqrt{5}$ ;

C. $\frac{3}{\sqrt{5}}$ ;

D. $2 \sqrt{2}$ .

Xem đáp án

Trong mặt phẳng tọa độ Oxy, cho điểm M(–3; 1) và đường tròn (C): x2 + y2 – 2x – 6y + 6 = 0 (ảnh 2)

Trong mặt phẳng tọa độ Oxy, cho điểm M(–3; 1) và đường tròn (C): x2 + y2 – 2x – 6y + 6 = 0 (ảnh 3)

Câu 10:

Cho đường tròn (C) có tâm I(1; 3) và bán kính $R = \sqrt{52}$ và điểm M có tọa độ nguyên thuộc đường thẳng $d : \{\begin{cases} x = 3 + 2 t \\ y = 1 - 4 t \end{cases} .$ Phương trình tiếp tuyến d’ của đường tròn (C) tại điểm M là

A. x + 2y + 3 = 0;

B. 2x + 5y + 21 = 0;

C. 2x – 3y – 19 = 0;

D. Đáp án khác.

Xem đáp án

Trắc nghiệm Toán 10 Bài 21. Đường tròn trong mặt phẳng tọa độ có đáp án

Dạng 3. Phương trình tiếp tuyến của đường tròn

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương