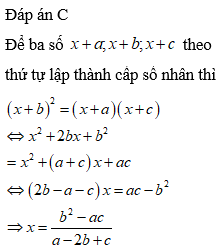21 câu hỏi trắc nghiệm thuộc Dựa vào tính chất của cấp số nhân, chứng minh đẳng thức, giải phương trình và ứng dụng bài toán thực tế

Câu 1:

Ba số 2x, 3x+3, 5x+5 theo thứ tự là ba số hạng liên tiếp của một cấp số nhân. Biết x khác -1, số hạng tiếp theo của cấp số nhân đó là

A. $- \frac{250}{3}$

B. $\frac{250}{3}$

C. 250

D. -250

Xem đáp án

Câu 2:

Cho cấp số nhân -4; x; -9 thì giá trị x là

A. $\pm 5$

B. -6,5

C. $\pm 6$

D. $\pm 36$

Xem đáp án

Đáp án C

Ta có

x^{2} = (- 4) (- 9) = 36 \Rightarrow x = \pm 6

Câu 3:

Cho cấp số nhân có bốn số hạng -2; x; -18; y. Hãy chọn kết quả đúng

A. x = -6; y = 54

B. x = 6; y = -54

C. x = -6; y = -54

D. x = -10; y = -26

Xem đáp án

Đáp án C

Ta có $\{\begin{matrix} x^{2} = (- 2) (- 18) = 36 \Rightarrow x = \pm 6 \\ x y = {(- 18)}^{2} = 324 \end{matrix} \Rightarrow [\begin{matrix} \{\begin{matrix} x = 6 \\ y = 54 \end{matrix} \\ \{\begin{matrix} x = - 6 \\ y = - 54 \end{matrix} \end{matrix}$

Câu 4:

Giá trị của x để 3 số 2x-1; x; 2x+1 theo thứ tự lập thành cấp số nhân là

A. $x = \pm \frac{1}{3}$

B. $x = \pm \sqrt{3}$

C. $x = \pm \frac{1}{\sqrt{3}}$

D. $x = \pm 1$

Xem đáp án

Đáp án C

Ta có

x^{2} = 4 x^{2} - 1 \Leftrightarrow 3 x^{2} = 1 \Leftrightarrow x = \pm \frac{1}{\sqrt{3}}

Câu 5:

Ba số x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 đồng thời các số x; 2y; 3z theo thứ tự lập thành một cấp số cộng với công sai khác 0. Giá trị của q là

A. $q = \frac{1}{3}$

B. $q = \frac{1}{9}$

C. $q = - \frac{1}{3}$

D. q = -3

Xem đáp án

Đáp án A

Vì x, y, z theo thứ tự lập thành một cấp số nhân với công bội q khác 1 nên $y = x . q; z = x . q^{2}$ (1)

Các số x, 2y, 3z theo thứ tự lập thành một cấp số nhân nên $x + 3 z = 4 y$ (2)

Thay (1) vào (2) được

$x + 3 x q^{2} = 4 x q \Leftrightarrow x (3 q^{2} - 4 q + 1) = 0 \Rightarrow 3 q^{2} - 4 q + 1 = 0 \Leftrightarrow [\begin{matrix} q = 1 \\ q = \frac{1}{3} \end{matrix}$

Vì $q \neq 1 nên q = \frac{1}{3}$

Câu 6:

Nếu ba số x+a; x+b; x+c theo thứ tự lập thành một cấp số nhân thì giá trị của x tính theo a, b, c là

A. $x = \frac{a^{2} - b c}{2 a - b - c}$

B. $x = \frac{c^{2} - a b}{a + b - 2 c}$

C. $x = \frac{b^{2} - a c}{a - 2 b + c}$

D. $x = \frac{a^{2} + b^{2} + c^{2}}{a + b + c}$

Xem đáp án

Câu 7:

Cho cấp số nhân

\frac{- 1}{5}, x, \frac{- 1}{125}

. Giá trị của x là

A. $\pm \frac{1}{\sqrt{5}}$

B. $\pm \frac{1}{25}$

C. $\pm \frac{1}{5}$

D. $\pm 5$

Xem đáp án

Đáp án B

\frac{- 1}{5}; x; \frac{- 1}{125}

là cấp số nhân khi và chỉ khi

x^{2} = \frac{1}{5} . \frac{1}{125} \Leftrightarrow x = \pm \frac{1}{25}

Câu 8:

Với giá trị nào của x thì 3 số x-2; x+1; 3-x lập thành cấp số nhân?

A. $\pm 1$

B. 2

C. -3

D. Không có giá trị nào

Xem đáp án

Câu 9:

Bốn số a, b, c, d theo thứ tự lập thành một cấp số cộng và bốn số a+1; b+1; c+3; d+9 theo thứ tự lập thành một cấp số nhân. Tổng a + d bằng

A. 6

B. 8

C. 10

D. 12

Xem đáp án

Đáp án B

Gọi m là công sai của cấp số cộng

Khi đó b=a+m; c=a+2m; d=a+3m

Do a+1; b+1; c+3; d+9 theo thứ tự lập thành một cấp số nhân nên $\{\begin{matrix} (a + 1) (c + 3) = {(b + 1)}^{2} \\ (b + 1) (d + 9) = {(c + 3)}^{2} \end{matrix}$

Thay $b = a + m; c = a + 2 m, d = a + 3 m$ vào hệ trên và rút gọn ta được $\{\begin{matrix} 2 a + 2 = m^{2} \\ 4 a = m^{2} \end{matrix} \Leftrightarrow \{\begin{matrix} a = 1 \\ [\begin{matrix} m = 2 \\ m = - 2 \end{matrix} \end{matrix}$

Thử lại ta thấy chỉ có trường hợp a=1; m=2 thỏa mãn

Vậy a+d=2a+3m=8

Câu 10:

Có bao nhiêu cấp số nhân gồm bốn phần tử mà tổng của chúng bằng 45 và số hạng thứ tư bằng bốn lần số hạng thứ 2?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án C

Ta có

\{\begin{matrix} S_{4} = 45 \\ u_{4} = 4 u_{2} \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} . \frac{q^{4} - 1}{q - 1} = 45 \\ u_{1} . q^{3} = 4 u_{1} . q \Rightarrow [\begin{matrix} q = 0 \\ q^{2} = 4 \end{matrix} \end{matrix} \Rightarrow [\begin{matrix} q = 0; u_{1} = 45 \\ q = 2; u_{1} = 3 \\ q = - 2; u_{1} = - 95 \end{matrix}

Câu 11:

Trong một cấp số nhân có các số hạng đều dương, hiệu của số hạng thứ năm và thứ tư là 576, hiệu của số hạng thứ hai và số hạng đầu là 9. Tổng 5 số hạng đầu tiên của cấp số nhân đó bằng

A. 768

B. 1024

C. 1023

D. 1061

Xem đáp án

Đáp án C

$\{\begin{matrix} u_{5} - u_{4} = 576 \\ u_{2} - u_{1} = 9 \end{matrix} \Leftrightarrow \{\begin{matrix} u_{1} . q^{4} - u_{1} . q^{3} = 576 \\ u_{1} . q - u_{1} = 9 \end{matrix} \Rightarrow \frac{q^{4} - q^{3}}{q - 1} = \frac{576}{9} \Rightarrow q^{3} = 64 \Leftrightarrow q = 4 \Rightarrow u_{1} = 3$

Vậy tổng 5 số hạng đầu là $S_{5} = u_{1} \frac{q^{5} - 1}{q - 1} = 1023$

Câu 12:

Ba số -x; 3; y theo thứ tự lập thành cấp số cộng, ba số 1; x; y theo thứ tự lập thành một cấp số nhân. Biết rằng x<0, khi đó tích xy bằng

A. 8

B. -27

C. -8

D. 5

Xem đáp án

Đáp án C

Ba số -x; 3; y theo thứ tự lập thành cấp số cộng nên -x+y=6 (1)

Ba số 1; x; y theo thứ tự lập thành cấp số nhân nên $x^{2} = y$ (2)

Từ (1), (2) và x<0 suy ra

\{\begin{matrix} x = - 2 \\ y = 4 \end{matrix} \Rightarrow x . y = - 8

Câu 13:

Cho bộ số $x_{0}, y_{0}, z_{0}$ là nghiệm của hệ phương trình $\{\begin{matrix} x + y + z = a + 4 \\ 2 x - y + 2 z = 2 a + 2 \\ 3 x + 2 y - 3 z = 1 - 2 a \end{matrix}$ . Các giá trị dương của a để $x_{0}, y_{0}, z_{0}$ lập thành một cấp số nhân là

A. a=1

B. a=2

C. a=3

D. a=4

Xem đáp án

Đáp án C

Giải hệ phương trình ta được $x_{0} = \frac{a + 3}{6}; y_{0} = 2; z_{0} = \frac{5 a + 9}{6}$

Để $x_{0}, y_{0}, z_{0}$ theo thứ tự lập thành một cấp số nhân thì

$x_{0} . z_{0} = y_{0}^{2} \Leftrightarrow \frac{a + 3}{6} . \frac{5 a + 9}{6} = 4 \Leftrightarrow 5 a^{2} + 24 a - 117 = 0 \Leftrightarrow [\begin{matrix} a = 3 \\ a = - \frac{39}{5} \end{matrix}$

Do a>0 nên a=3

Câu 14:

Tất cả các giá trị thực của tham số m để phương trình

x^{3} - 3 m x^{2} - (m + 1) x - 2 = 0

có ba nghiệm phân biệt lập thành một cấp số nhân là

A. $m = - \frac{5}{\sqrt[3]{2} + 1}$

B. $m = - \frac{5}{3 \sqrt[3]{2} + 1}$

C. $m = \frac{5}{3 \sqrt[3]{2} + 1}$

D. $m = \frac{5}{3 \sqrt[3]{2} - 1}$

Xem đáp án

Câu 15:

Ba số a, b, c theo thứ tự là số hạng thứ nhất, số hạng thứ hai và số hạng thứ ba của một cấp số nhân, đồng thời cũng lần lượt là số hạng thứ nhất, số hạng thứ hai và số hạng thứ tư của một cấp số cộng có công sai bằng 10. Giá trị của a là

A. a = 5

B. $a = \frac{10}{3}$

C. a = 10

D. $a = - \frac{10}{3}$

Xem đáp án

Đáp án C

Theo đề bài ta có $a = u_{1}; b = u_{2} = u_{1} + 10; c = u_{4} = u_{1} + 30$

Theo tính chất cấp số nhân, ta có $b^{2} = a . c \Leftrightarrow {(u_{1} + 10)}^{2} = u_{1} (u_{1} + 30) \Leftrightarrow u_{1} = 10 \Rightarrow a = 10$

Câu 16:

Cho ba số

\frac{\sin α}{6}, \cos α, \tan α

theo thứ tự lập thành một cấp số nhân, với

- \frac{π}{2} \leq α \leq 0

. Khi đó giá trị

\cos 2 α

bằng

A. $\frac{1}{2}$

B. $\frac{\sqrt{3}}{2}$

C. $- \frac{\sqrt{3}}{2}$

D. $- \frac{1}{2}$

Xem đáp án

Đáp án D

Theo giả thiết ta có $\frac{\sin α}{6} . \tan α = {(\cos α)}^{2} \Leftrightarrow \frac{{(\sin α)}^{2}}{6. \cos α} = {(\cos α)}^{2} \Leftrightarrow 6. {(\cos α)}^{3} + {(\cos α)}^{2} - 1 = 0 \Leftrightarrow \cos α = \frac{1}{2}$

Từ đó $\cos 2 α = 2 {(\cos α)}^{2} - 1 = - \frac{1}{2}$

Câu 17:

Người ta thiết kế một cái tháp gồm 11 tầng. Diện tích bề mặt trên của mỗi tầng bằng nửa diện tích mặt trên của tầng ngay bên dưới và diện tích mặt trên của tầng 1 bằng nửa diện tích đế tháp. Biết diện tích đáy tháp là

12288 m^{2}

, diện tích mặt trên cùng bằng

A. $8 m^{2}$

B. $6 m^{2}$

C. $12 m^{2}$

D. $10 m^{2}$

Xem đáp án

Đáp án B

Ta nhận thấy diện tích các mặt trên của mỗi tầng lập thành 1 cấp số nhân với công bội q

Số hạng đầu $u_{1} = 12288$ . Khi đó mặt trên cùng tầng 11 ứng với $u_{12}$

Do đó

u_{12} = u_{1} . q^{11} = 1288. {(\frac{1}{2})}^{11} = 6

Câu 18:

Một khu rừng có trữ lượng gỗ là

{6.10}^{5} (m^{3})

. Biết tốc độ sinh trưởng của các cây trong rừng là 4,5% mỗi năm. Hỏi sau 10 năm, khu rừng đó sẽ có bao nhiêu m³ gỗ (làm tròn đến hàng đơn vị)?

A. $931782 m^{3}$

B. $931781 m^{3}$

C. $891657 m^{3}$

D. $891658 m^{3}$

Xem đáp án

Câu 19:

Bạn An thả quả bóng cao su từ độ cao 10m theo phương thẳng đứng. Mỗi khi chạm đất nó lại nảy lên theo phương thẳng đứng với độ cao bằng

\frac{3}{4}

độ cao trước đó. Tổng quãng đường bóng đi được đến khi bóng dừng hẳn là

A. 40m

B. 70m

C. 50m

D. 80m

Xem đáp án

Câu 20:

Cho ba số thực dương a, b, c là ba số hạng liên tiếp của một cấp số nhân đồng thời thỏa mãn điều kiện

\frac{a^{2} b^{2} c^{2}}{a^{3} + b^{3} + c^{3}} = 4

. Giá trị của biểu thức

P = \frac{1}{a^{3}} + \frac{1}{b^{3}} + \frac{1}{c^{3}}

là

A. P = 4

B. P = 2

C. $P = \frac{1}{2}$

D. $P = \frac{1}{4}$

Xem đáp án

Đáp án D

Ta có $\frac{a^{2} b^{2} c^{2}}{a^{3} + b^{3} + c^{3}} = 4 \Leftrightarrow \frac{1}{4} = \frac{a^{3} + b^{3} + c^{3}}{a^{2} b^{2} c^{2}} = \frac{a}{b^{2} c^{2}} + \frac{b}{c^{2} a^{2}} + \frac{c}{a^{2} b^{2}}$

Mặt khác a, b, c là ba số hạng liên tiếp của một cấp số nhân nên $a c = b^{2}$

Do đó

$\frac{1}{4} = \frac{a}{b^{2} c^{2}} + \frac{b}{c^{2} a^{2}} + \frac{c}{a^{2} b^{2}} = \frac{a}{a c^{3}} + \frac{b}{b^{4}} + \frac{c}{a^{3} c} = \frac{1}{a^{3}} + \frac{1}{b^{3}} + \frac{1}{c^{3}} \Rightarrow P = \frac{1}{4}$

Câu 21:

Các giá trị m để phương trình

x^{3} + 2 x^{2} + (m + 1) x + 2 (m + 1) = 0

có ba nghiệm lập thành một cấp số nhân là

A. m=-1; m=-3; m=-4

B. m=-1; m=13; m=-4

C. m=1; m=3; m=4

D. Không có giá trị của m

Xem đáp án

Đáp án D

Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số nhân

Khi đó $\{\begin{matrix} x_{1} x_{3} = x_{2}^{2} \\ x_{1} + x_{2} + x_{3} = - 2 \\ x_{1} x_{2} + x_{2} x_{3} + x_{3} x_{1} = m + 1 \end{matrix} \Rightarrow x_{2} = - \frac{m + 1}{2}$

Thay vào phương trình ta được m=-1; m=3; m=-4

Thay từng giá trị của m vào phương trình ta thấy không có giá trị nào của m thỏa mãn yêu cầu bài toán

Bài tập chuyên đề Toán 11 Bài 3: Cấp số nhân

Dựa vào tính chất của cấp số nhân, chứng minh đẳng thức, giải phương trình và ứng dụng bài toán thực tế

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương