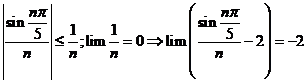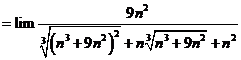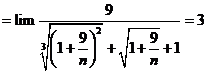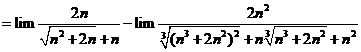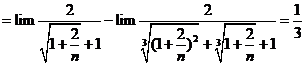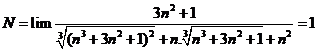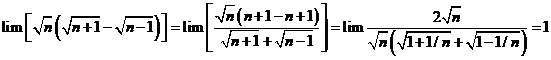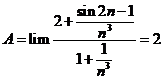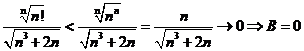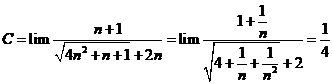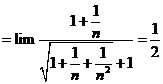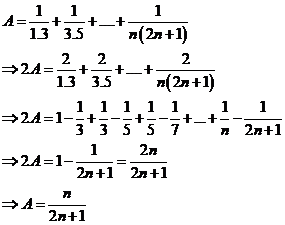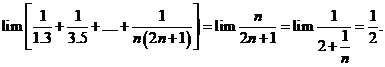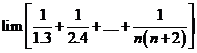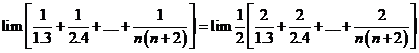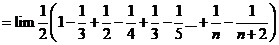Trắc nghiệm Toán 11 Bài 2: Giới hạn dãy số có đáp án (Mới nhất)
Trắc nghiệm Toán 11 Bài 2: Giới hạn dãy số có đáp án (Mới nhất)
-
114 lượt thi
-
105 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 6:
Giá trị của ![]() bằng:
bằng:
 Xem đáp án
Xem đáp án
Chọn B.
Với mọi số dương M lớn tùy ý ta chọn nM thỏa ![]()
![]() .
.
Ta có: ![]()
Vậy ![]() .
.
Câu 19:
Giá trị của ![]() bằng:
bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Gọi m là số tự nhiên thỏa: ![]() . Khi đó với mọi
. Khi đó với mọi ![]()
Ta có: 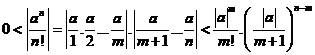
Mà 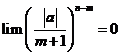 . Từ đó suy ra:
. Từ đó suy ra: ![]() .
.
Câu 20:
Giá trị của ![]() với a > 0 bằng:
với a > 0 bằng:
 Xem đáp án
Xem đáp án
Chọn D.
Nếu a = 1 thì ta có đpcm
Giả sử a > 1. Khi đó: 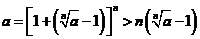
Suy ra: ![]() nên
nên ![]()
Với 0 < a < 1 thì ![]() .
.
Tóm lại ta luôn có: ![]() với a > 0.
với a > 0.
Câu 21:
Cho dãy số (un) với ![]() và
và ![]() . Chọn giá trị đúng của trong các số sau:
. Chọn giá trị đúng của trong các số sau:
 Xem đáp án
Xem đáp án
Chọn C.
Chứng minh bằng phương pháp quy nạp toán học ta có ![]()
Nên ta có: ![]()
Suy ra: ![]() , mà
, mà ![]() .
.
Câu 43:
Giá trị của ![]() (Trong đó k; p là các số nguyên dương;
(Trong đó k; p là các số nguyên dương; ![]() ) bằng:
) bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Ta xét ba trường hợp sau
k > p. Chia cả tử và mẫu cho nk ta có: 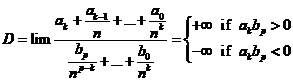
k = p . Chia cả tử và mẫu cho nk ta có: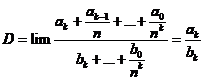 .
.
k < p. Chia cả tử và mẫu cho np: 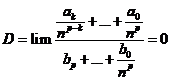 .
.
Câu 52:
Cho các số thực a,b thỏa ![]() . Tìm giới hạn
. Tìm giới hạn ![]() .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có ![]() là một cấp số nhân công bội
là một cấp số nhân công bội ![]()
Tương tự ![]()
Suy ra lim 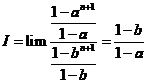
( Vì ![]()
![]() ).
).
Câu 53:
Tính giới hạn của dãy số ![]() với
với ![]()
 Xem đáp án
Xem đáp án
Chọn C.
Ta chia làm các trường hợp sau
TH 1: n = k, chia cả tử và mẫu cho nk, ta được 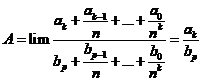 .
.
TH 2: k > p, chia cả tử và mẫu cho nk, ta được 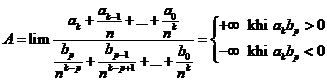
TH 3: k < p, chia cả tử và mẫu cho np, ta được ![]() .
.
Câu 86:
Cho dãy số (xn) xác định bởi ![]()
Đặt ![]() . Tính Sn.
. Tính Sn.
 Xem đáp án
Xem đáp án
Chọn C.
Từ công thức truy hồi ta có: ![]()
Nên dãy (xn) là dãy số tăng.
Giả sử dãy (xn) là dãy bị chặn trên, khi đó sẽ tồn tại ![]()
Với x là nghiệm của phương trình: ![]() vô lí
vô lí
Do đó dãy (xn) không bị chặn, hay ![]() .
.
Mặt khác: ![]()
Suy ra: ![]()
Dẫn tới: ![]()
Câu 87:
Cho dãy (xk) được xác định như sau: ![]()
Tìm un với ![]() .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: ![]() nên
nên ![]()
Suy ra ![]()
Mà: ![]()
Mặt khác: ![]()
Vậy ![]() .
.
Câu 88:
Cho dãy số (xn) được xác định bởi: 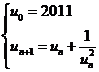 . Tìm
. Tìm ![]() .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta thấy ![]()
Ta có: ![]() (1)
(1)
Suy ra: ![]() (2)
(2)
Từ (1) và (2), suy ra: 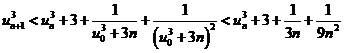
Do đó: ![]() (3)
(3)
Lại có: ![]() .
.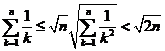
Nên: ![]()
Hay ![]() .
.
Vậy ![]() .
.
Câu 89:
Cho dãy x > 0 xác định như sau: ![]() . Tìm .
. Tìm .
 Xem đáp án
Xem đáp án
Chọn C.
Ta có ![]()
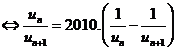
Ta có ![]()
Mặt khác ta chứng minh được: ![]() .
.
Nên ![]() .
.
Câu 96:
Gọi ![]() là dãy số xác định bởi
là dãy số xác định bởi ![]() . Tìm
. Tìm ![]() .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có ![]() nên dãy (un)là dãy tăng.
nên dãy (un)là dãy tăng.
Dễ dàng chứng minh được ![]() .Từ đó tính được
.Từ đó tính được ![]() .
.
Câu 97:
Cho dãy số ![]() được xác định như sau
được xác định như sau ![]() .
.
Đặt ![]() . Tìm
. Tìm ![]() .
.
 Xem đáp án
Xem đáp án
Chọn C.
Ta có: ![]()
![]()
Suy ra: ![]()
Suy ra: ![]()
Do đó, suy ra: 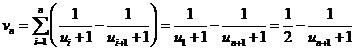
Mặt khác, từ ![]() ta suy ra:
ta suy ra: ![]() .
.
Nên 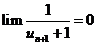 . Vậy
. Vậy ![]() .
.
Câu 98:
Cho 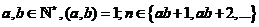 . Kí hiệu rn là số cặp số
. Kí hiệu rn là số cặp số ![]() sao cho
sao cho ![]() . Tìm .
. Tìm .![]()
 Xem đáp án
Xem đáp án
Chọn C.
Xét phương trình ![]() (1).
(1).
Gọi ![]() là một nghiệm nguyên dương của (1). Giả sử (u; v) là một nghiệm nguyên dương khác
là một nghiệm nguyên dương của (1). Giả sử (u; v) là một nghiệm nguyên dương khác ![]() của (1).
của (1).
Ta có ![]() suy ra
suy ra ![]() do đó tồn tại k nguyên dương sao cho
do đó tồn tại k nguyên dương sao cho ![]() . Do v là số nguyên dương nên
. Do v là số nguyên dương nên ![]() . (2)
. (2)
Ta nhận thấy số nghiệm nguyên dương của phương trình (1) bằng số các số k nguyên dương cộng với 1. Do đó ![]() .
.
Từ đó ta thu được bất đẳng thức sau: ![]()
Từ đó suy ra : ![]()
Từ đây áp dụng nguyên lý kẹp ta có ngay ![]() .
.
Câu 99:
Cho dãy số có giới hạn (un) xác định bởi: 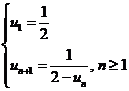 . Tìm kết quả đúng của lim un .
. Tìm kết quả đúng của lim un .
 Xem đáp án
Xem đáp án
Chọn B.
Ta có: ![]()
Dự đoán ![]() với
với ![]()
Dễ dàng chứng minh dự đoán trên bằng phương pháp quy nạp.
Từ đó 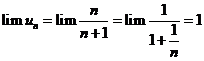 .
.
Câu 104:
Tính giới hạn: ![]() .
.
 Xem đáp án
Xem đáp án
Chọn A.
Cách 1:
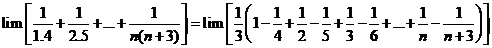
![]() .
.
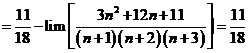
Cách 2: Bấm máy tính như sau: ![]() và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
Câu 105:
Tính giới hạn: ![]() .
.
 Xem đáp án
Xem đáp án
Chọn B.
Cách 1:
Cách 2: Bấm máy tính như sau: ![]() và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).
và so đáp án (có thể thay 100 bằng số nhỏ hơn hoặc lớn hơn).

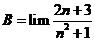
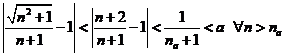
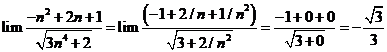
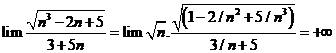
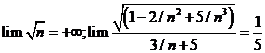
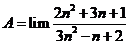
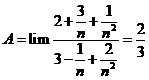
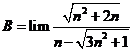
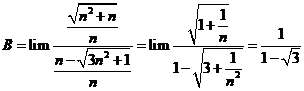
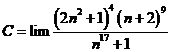
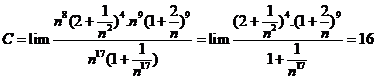
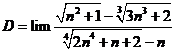
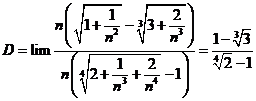
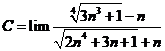
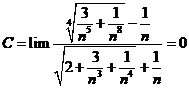 .
.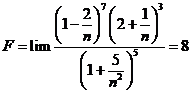
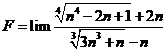
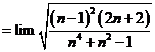
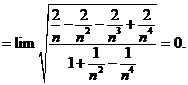
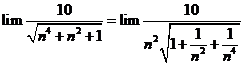
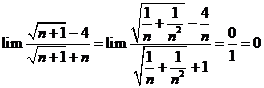
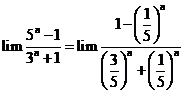
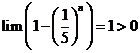 ,
,