Câu hỏi:
03/04/2024 63Xếp ngẫu nhiên 10 học sinh gồm 2 học sinh lớp A, 3 học sinh lớp B và 5 học sinh lớp C thành một hàng ngang. Xác suất để không có học sinh lớp B nào xếp giữa hai học sinh lớp A bằng
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C
Số cách xếp ngẫu nhiên là 10! cách.
Ta tìm số cách xếp thoả mãn:
* Trước tiên xếp 2 học sinh lớp A có 2! cách.
Vì giữa hai học sinh lớp A không có học sinh lớp B nên chỉ có thể xếp học sinh lớp C vào giữa hai học sinh lớp A vừa xếp:
* Vậy chọn ![]() học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có cách, ta được một nhóm X.
học sinh lớp C rồi xếp vào giữa hai học sinh lớp A có cách, ta được một nhóm X.
* Xếp ![]() học sinh còn lại với nhóm X có (9-k)! cách.
học sinh còn lại với nhóm X có (9-k)! cách.
Vậy tất cả có 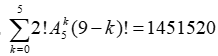 cách xếp thỏa mãn.
cách xếp thỏa mãn.
Xác suất cần tính bằng ![]()
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Người ta sắp xếp ngẫu nhiên 5 viên bi được đánh số từ 1 đến 5 vào năm chiếc hộp theo một hàng ngang. Tính xác suất để các viên bi được đánh số chẵn luôn đứng cạnh nhau.
Câu 2:
Có 3 quyển sách Văn học khác nhau, 4 quyển sách Toán học khác nhau và 7 quyển sách Tiếng Anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau
Câu 3:
Sắp xếp 5 quyển sách Toán và 4 quyển sách Văn lên một kệ sách dài. Tính xác suất để các quyển sách cùng một môn nằm cạnh nhau.
Câu 4:
Có 2 học sinh lớp A, 3 học sinh lớp B và 4 học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh lớp B. Hỏi có bao nhiêu cách sắp xếp như vậy?
Câu 5:
Xếp ngẫu nhiên 5 bạn An, Bình, Cường, Dũng, Đông ngồi vào một dãy 5 ghế thẳng hàng (mỗi bạn ngồi 1 ghế). Xác suất của biến cố “hai bạn An và Bình không ngồi cạnh nhau” là:
Câu 6:
Xếp ngẫu nhiên tám học sinh gồm bốn học sinh nam (trong đó có Hoàng và Nam) cùng bốn học sinh nữ (trong đó có Lan) thành một hàng ngang. Xác suất để trong tám học sinh trên không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Lan đứng cạnh Hoàng và Nam là
Câu 7:
Có 3 quyển sách toán, 4 quyển sách lí và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách gồm có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong ba ngăn (mỗi ngăn đủ rộng để chứa tất cả quyển sách). Tính xác suất để không có bất kì hai quyển sách toán nào đứng cạnh nhau.
Câu 8:
Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ, ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau bằng
Câu 9:
Bạn Nam làm bài thi thử THPT Quốc gia môn Toán có 50 câu, mỗi câu có 4 đáp án khác nhau, mỗi câu đúng được 0,2 điểm, mỗi câu làm sai hoặc không làm không được điểm cũng không bị trừ điểm. Bạn Nam đã làm đúng được 40 câu còn 10 câu còn lại bạn chọn ngẫu nhiên mỗi câu một đáp án. Xác suất để bạn Nam được trên điểm gần với số nào nhất trong các số sau?
Câu 10:
Xếp chỗ cho 6 học sinh trong đó có học sinh A và 3 thầy giáo vào 9 ghế kê thành hàng ngang (mỗi ghế xếp một người). Tính xác suất sao cho mỗi thầy giáo ngồi giữa 2 học sinh và học sinh A ngồi ở một trong hai đầu hàng.
Câu 11:
Đội thanh niên xung kích của một trường THPT gồm 15 học sinh trong đó có 4 học sinh khối 12, 5 học sinh khối 11 và 6 học sinh khối 10. Chọn ngẫu nhiên ra 6 học sinh đi làm nhiệm vụ. Tính xác suất để chọn được 6 học sinh đủ 3 khối.
Câu 12:
Một hộp chứa 10 quả cầu đỏ được đánh số từ 1 đến 10, 20 quả cầu xanh được đánh số từ 1 đến 20. Lấy ngẫu nhiên một quả. Khi đó xác suất để lấy được quả màu xanh hoặc ghi số lẻ bằng
Câu 13:
Một hộp chứa 15 quả cầu đỏ được đánh số từ 1 đến 15, 20 quả cầu xanh được đánh số từ 1 đến 20. Lấy ngẫu nhiên đồng thời hai quả. Khi đó xác suất để hai quả cầu lấy được đều màu đỏ hoặc đều ghi số chẵn bằng
Câu 14:
Một hộp kín chứa 50 quả bóng kích thước bằng nhau, được đánh số từ 1 đến 50. Bốc ngẫu nhiên cùng lúc 2 quả bóng từ hộp trên. Gọi P là xác suất bốc được 2 quả bóng có tích của 2 số ghi trên 2quả bóng là một số chia hết cho 10, khẳng định nào sau đây đúng?
Câu 15:
Gọi X là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Lấy ngẫu nhiên một số trong tập hợp X. Gọi A là biến cố lấy được số có đúng hai chữ số 1, có đúng hai chữ số 2, bốn chữ số còn lại đôi một khác nhau, đồng thời các chữ số giống nhau không đứng liền kề nhau. Xác suất của biến cố A bằng


