Câu hỏi:
03/04/2024 39Từ một tập gồm 10 câu hỏi trong đó có 4 câu lý thuyết và 6 câu bài tập, người ta tạo thành các đề thi. Biết rằng một đề thi phải gồm 3 câu hỏi trong đó có ít nhất một câu lý thuyết và một câu bài tập. Hỏi có thể tạo bao nhiêu đề khác nhau ?
A. 96
B. 100
C. 60
D. 36
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A
Xảy ra hai trường hợp
TH1 : 2 câu lý thuyết, 1 câu bài tập có ![]() .
.
TH2 : 1 câu lý thuyết, 2 câu bài tập có ![]() .
.
Vậy có thể tạo 60 + 36 = 96A. 96 đề khác nhau.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Bé Minh có một bảng hình chữ nhật gồm 6 hình vuông đơn vị, cố định không xoay như hình vẽ. Bé muốn dùng 3 màu để tô tất cả các cạnh của các hình vuông đơn vị, mỗi cạnh tô một lần sao cho hình vuông đơn vị được tô bởi đúng 2 màu, trong đó mỗi màu tô đúng hai cạnh. Hỏi bé Minh có tất cả bao nhiêu cách tô màu bảng?
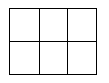
Câu 2:
Có bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau, sao cho trong mỗi số đó nhất thiết phải có mặt chữ số 0?
Câu 3:
Cho đa giác đều có 20 cạnh. Có bao nhiêu hình chữ nhật (không phải là hình vuông), có các đỉnh là đỉnh của đa giác đều đã cho?
Câu 4:
Gieo 2 xúc xắc màu xanh và đỏ cùng 1 lần. Hỏi có bao nhiêu khả năng xảy ra số chấm xuất hiện của xúc xắc màu xanh nhiều hơn số chấm xuất hiện trên xúc xắc màu đỏ.
Câu 5:
Có 6 học sinh và 3thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế. Số cách xếp chỗ ngồi cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là
Câu 6:
Có bao nhiêu cách bỏ đồng thời 7 quả bóng bàn giống nhau vào 4 hộp khác nhau sao cho mỗi hộp có ít nhất 1 quả?
Câu 7:
Với k, n là hai số nguyên dương tùy ý thỏa mãn k ≤ n, mệnh đề nào dưới đây sai?
Câu 9:
Từ các chữ số 1,2,3,4,5,6 lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau?
Câu 13:
Đề kiểm tra 15 phút có 10 câu trắc nghiệm, mỗi câu có bốn phương án trả lời, trong đó có một phương án đúng, mỗi câu trả lời đúng được 1,0 điểm. Một thí sinh làm cả 10 câu, mỗi câu chọn một phương án. Tính xác suất để thí sinh đó đạt từ 8,0 điểm trở lên.
Câu 14:
Cho các số nguyên dương tùy ý k, n thỏa mãn kn. Đẳng thức nào dưới đây đúng ?
Câu 15:
Cho A = {1,2,3,4}. Từ A lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau?


