Giải SGK Toán 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu
1. Hằng đẳng thức
Luyện tập 1 trang 30 Toán 8 Tập 1: Trong các đẳng thức sau, đẳng thức nào là hằng đẳng thức?
a) a(a+2b)=a2+2ab
b) a+1=3a−1
Phương pháp giải:
Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
Lời giải:
a) a(a+2b)=a2+2ab là hằng đẳng thức.
b) a+1=3a−1 không là hằng đẳng thức vì khi ta thay a=2 thì hai vế của đẳng thức không bằng nhau.
2. Hiệu hai bình phương
HĐ 1 trang 30 Toán 8 Tập 1: Quan sát Hình 2.1
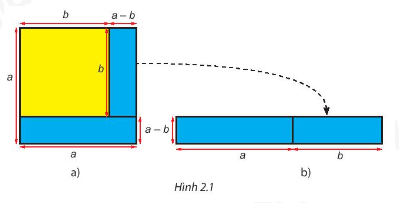
a) Tính diện tích của phần hình màu xanh ở Hình 2.1a.
b) Tính diện tích hình chữ nhật màu xanh ở Hình 2.1b.
c) Có nhận xét gì về diện tích của hai hình ở câu a và câu b?
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Lời giải:
a) Diện tích của phần hình màu xanh ở Hình 2.1a là: a2−b2.
b) Diện tích hình chữ nhật màu xanh ở Hình 2.1b là: (a+b)(a−b).
c) Diện tích hai hình ở câu a và b bằng nhau.
HĐ 2 trang 31 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính (a+b)(a−b).
Từ đó rút ra liên hệ giữa a2−b2 và (a+b)(a−b).
Phương pháp giải:
Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.
Lời giải:
(a+b)(a−b)=a.a−ab+b.a−b.b=a2−b2+(−ab+ba)=a2−b2
Từ đó ta được a2−b2=(a+b)(a−b)
Luyện tập 2 trang 31 Toán 8 Tập 1: a) Tính nhanh 992−1
b) Viết x2−9 dưới dạng tích.
Phương pháp giải:
Sử dụng hằng đẳng thức a2−b2=(a+b)(a−b)
Lời giải:
a) 992−1=992−12=(99+1).(99−1)=100.98=9800.
b) x2−9=x2−32=(x+3).(x−3)
Phương pháp giải:
Sử dụng hằng đẳng thức a2−b2=(a+b)(a−b)
Lời giải:
198.202=(200−2).(200+2)=2002−22=400−4=396.
3. Bình phương của một tổng
HĐ 3 trang 31 Toán 8 Tập 1: Với hai số a,b bất kì, thực hiện phép tính (a+b).(a+b).
Từ đó rút ra liên hệ giữa (a+b)2 và a2+2ab+b2
Phương pháp giải:
Muốn nhân hai đa thức ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả với nhau.
Lời giải:
(a+b).(a+b)=a.a+a.b+b.a+b.b=a2+(ab+ab)+b2=a2+2ab+b2
Từ đó ta được (a+b)2=a2+2ab+b2
Luyện tập 3 trang 32 Toán 8 Tập 1: 1. Khai triển (2b+1)2
2. Viết biểu thức 9y2+6yx+x2 dưới dạng bình phương của một tổng.
Phương pháp giải:
Sử dụng hằng đẳng thức (a+b)2=a2+2ab+b2
Lời giải:
1. (2b+1)2=(2b)2+2.2b.1+12=4b2+4b+1
2. 9y2+6yx+x2=(3y)2+2.3y.x+x2=(3y+x)2
4. Bình phương của một hiệu
Phương pháp giải:
Sử dụng hằng đẳng thức (a+b)2=a2+2ab+b2
Lời giải:
(a−b)2=[a+(−b)]2=a2+2.a.(−b)+(−b)2=a2−2.ab+b2
Luyện tập 4 trang 32 Toán 8 Tập 1: Khai triển (3x−2y)2
Phương pháp giải:
Sử dụng hằng đẳng thức (A−B)2=A2−2AB+B2
Lời giải:
(3x−2y)2=(3x)2−2.3x.2y+(2y)2=9x2−12xy+4y2
Phương pháp giải:
Sử dụng hằng đẳng thức (a+b)2=a2+2ab+b2
Lời giải:
10022=(1000+2)2=10002+2.1000.2+22=1000000+4000+4=1004004
Bài tập
Bài 2.1 trang 33 Toán 8 Tập 1: Những đẳng thức nào sau đây là hằng đẳng thức?
a) x+2=3x+1
b) 2x(x+1)=2x2+2x
c) (a+b)a=a2+ba
d) a−2=2a+1
Phương pháp giải
Hằng đẳng thức là đẳng thức mà hai vế luôn cùng nhận một giá trị khi thay các chữ trong đẳng thức bằng các số tùy ý.
Lời giải:
a) x+2=3x+1 không là hằng đẳng thức vì khi ta thay x=0 thì hai vế của đẳng thức không bằng nhau.
b) 2x(x+1)=2x2+2x là hằng đẳng thức.
c) (a+b)a=a2+balà hằng đẳng thức.
d) a−2=2a+1 không là hằng đẳng thức vì khi ta thay a=0 thì hai vế của đẳng thức không bằng nhau.
Bài 2.2 trang 33 Toán 8 Tập 1: Thay ![]() bằng biểu thức thích hợp.
bằng biểu thức thích hợp.
a) (x−3y)(x+3y)=x2−?;
b) (2x−y)(2x+y)=4?−y2;
c) x2+8xy+?=(?+4y)2;
d) ?−12xy+9y2=(2x−?)2.
Phương pháp giải
Sử dụng ba hằng đẳng thức:
+)A2−B2=(A+B)(A−B)+)(A+B)2=A2+2AB+B2+)(A−B)2=A2−2AB+B2
Lời giải:
a) (x−3y)(x+3y)=x2−9y2;
b) (2x−y)(2x+y)=4x2−y2;
c) x2+8xy+16y2=(x+4y)2;
d) 4x2−12xy+9y2=(2x−3y)2.
Bài 2.3 trang 33 Toán 8 Tập 1: Tính nhanh:
a) 54.66;
b) 2032.
Phương pháp giải
Sử dụng 2 hằng đẳng thức:
+)A2−B2=(A+B)(A−B)+)(A+B)2=A2+2AB+B2
Lời giải:
a) 54.66=(60−6).(60+6)=602−62=3600−36=3564
b) 2032=(200+3)2=2002+2.200.3+32=40000+600+9=40609
a) x2+4x+4
b) 16a2−16ab+4b2
Phương pháp giải
Sử dụng 2 hằng đẳng thức:
+)(A+B)2=A2+2AB+B2+)(A−B)2=A2−2AB+B2
Lời giải:
a) x2+4x+4=x2+2.x.2+22=(x+2)2
b) 16a2−16ab+4b2=(4a)2−2.4a.2b+(2b)2=(4a−2b)2
Bài 2.5 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:
a) (x−3y)2−(x+3y)2
b) (3x+4y)2+(4x−3y)2
Phương pháp giải
Sử dụng ba hằng đẳng thức:
+)A2−B2=(A+B)(A−B)+)(A+B)2=A2+2AB+B2+)(A−B)2=A2−2AB+B2
Lời giải:
a) (x−3y)2−(x+3y)2=(x−3y+x+3y).(x−3y−x−3y)=(2x).(−6y)=−12xy
b)
(3x+4y)2+(4x−3y)2=(3x)2+2.3x.4y+(4y)2+(4x)2−2.4x.3y+(3y)2=9x2+24xy+16y2+16x2−24xy+9y2=(9x2+16x2)+(24xy−24xy)+(16y2+9y2)=25x2+25y2
Phương pháp giải
Sử dụng hằng đẳng thức a2−b2=(a+b)(a−b)
Nếu 2 số nguyên a, b thỏa mãn a chia hết cho 4 thì a.b chia hết cho 4.
Lời giải:
Ta có:
(n+2)2−n2=(n+2−n).(n+2+n)=2.(2n+2)=2.2.(n+1)=4.(n+1).
Vì 4⋮4 nên 4(n+1)⋮4 với mọi số tự nhiên n.
Xem thêm lời giải bài tập SGK Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
Bài 7: Lập phương của một tổng. Lập phương của một hiệu




