Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC. Chứng minh góc CBI > góc ACI

Bài 3 trang 111 Toán 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.

a) Chứng minh $\widehat{CBI}>\widehat{ACI}$;

b) So sánh IB và IC.

Trả lời

Chứng minh (Hình vẽ dưới đây):

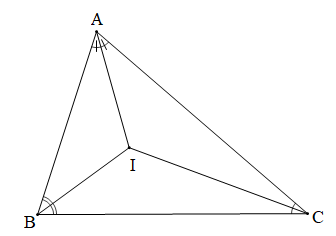
a) Vì BI là đường phân giác của $\widehat{ABC}$ nên $\widehat{ABI}=\widehat{CBI}=\frac{1}{2}\widehat{ABC}$.

Vì CI là đường phân giác của $\widehat{ACB}$ nên $\widehat{ACI}=\widehat{BCI}=\frac{1}{2}\widehat{ACB}$.

Tam giác ABC có AB < AC nên $\widehat{ACB}<\widehat{ABC}$ (quan hệ giữa góc và cạnh đối diện trong một tam giác)

Do đó $\frac{1}{2}\widehat{ACB}<\frac{1}{2}\widehat{ABC}$.

Suy ra $\widehat{ACI}<\widehat{CBI}$.

Vậy $\widehat{CBI}>\widehat{ACI}.$

b) Vì $\widehat{ACI}<\widehat{CBI}$ (chứng minh câu a), mà $\widehat{ACI}=\widehat{BCI}$ nên $\widehat{BCI}<\widehat{CBI}$.

Tam giác BIC có $\widehat{BCI}<\widehat{CBI}$ nên IB < IC (quan hệ giữa cạnh và góc đối diện trong một tam giác)

Vậy IB < IC.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 9: Đường trung trực của một đoạn thẳng

Bài 10: Tính chất ba đường trung tuyến của tam giác

Bài 11: Tính chất ba đường phân giác của tam giác

Bài 12: Tính chất ba đường trung trực của tam giác

Bài 13: Tính chất ba đường cao của tam giác

Bài tập cuối chương 7