Giải SGK Toán 11 (Kết nối tri thức) Bài 26: Khoảng cách

Giải Toán 11 Bài 26: Khoảng cách

1. Khoảng cách từ một điểm đến một đường thẳng , đến một mặt phẳng

HĐ1 trang 54 Toán 11 Tập 2:

a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, giải thích vì sao MK $\ge$ MH (H.7.74).

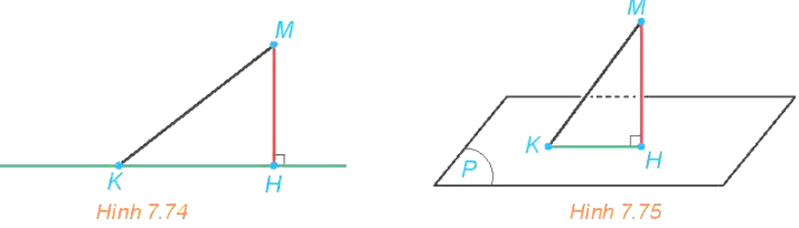
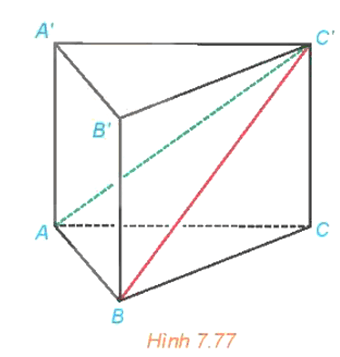
b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M lên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK $\ge$ MH (H7.75).

Lời giải:

a) Vì H là hình chiếu của M trên a nên MH $\perp$ a hay MH là đường vuông góc kẻ từ điểm M đến đường thẳng a. Khi đó MH là đường ngắn nhất nên MK $\ge$ MH.

b) Vì H là hình chiếu của M lên (P) nên MH $\perp$ (P), suy ra MH $\perp$ KH.

Dựa vào quan hệ giữa đường xiên và đường vuông góc ta có MK $\ge$ MH.

Luyện tập 1 trang 55 Toán 11 Tập 2: Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).

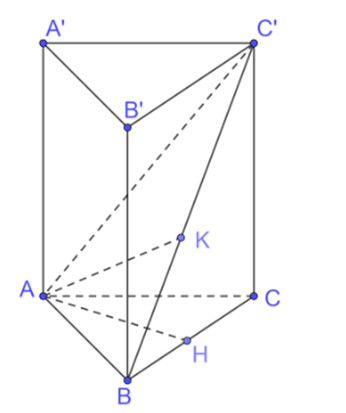
a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').

b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.

Lời giải:

a) Vì ABC.A'B'C' là hình lăng trụ đứng nên BB' $\perp$ (ABC) nên (BCC'B') $\perp$ (ABC).

Hạ AH $\perp$ BC tại H.

Có 

Khi đó AH chính là khoảng cách từ A đến mặt phẳng (BCC'B').

Vì tam giác ABC vuông cân tại A nên AB = AC = a.

Xét tam giác ABC vuông cân tại A, có

$\frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}=\frac{1}{a^2}+\frac{1}{a^2}=\frac{2}{a^2}$$\Rightarrow AH=\frac{a}{\sqrt{2}}$

Vậy khoảng cách từ A đến mặt phẳng (BCC'B') bằng $\frac{a}{\sqrt{2}}$.

b) Vì tam giác ABC vuông cân tại A nên AB $\perp$ AC.

Vì AA' $\perp$ (ABC) nên AA' $\perp$ AB mà AB $\perp$ AC nên AB $\perp$ (ACC'A'), suy ra AB $\perp$ AC'.

Do đó tam giác ABC' là tam giác vuông tại A.

Hạ AK $\perp$ BC' tại K. Khi đó d(A, BC') = AK.

Vì ACC'A' là hình chữ nhật nên $A{C^{\text{'}}}^2=A{A^{\text{'}}}^2+A^{\text{'}}{C^{\text{'}}}^2=h^2+a^2$ .

Xét tam giác ABC' vuông tại A, AK là đường cao, ta có:

$\frac{1}{A{K}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C^{\text{'}}}^2}=\frac{1}{a^2}+\frac{1}{a^2+h^2}$$=\frac{2a^2+h^2}{a^2\left(a^2+h^2\right)}$

$\Rightarrow$$A{K}^2=\frac{a^2\left(a^2+h^2\right)}{2a^2+h^2}$$\Rightarrow AK=a\sqrt{\frac{a^2+h^2}{2a^2+h^2}}$

Vậy khoảng cách từ A đến BC' bằng $a\sqrt{\frac{a^2+h^2}{2a^2+h^2}}$.

2. Khoảng cách giữa các đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

HĐ2 trang 55 Toán 11 Tập 2: Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M; N bất kỳ thuộc a và gọi A; B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).

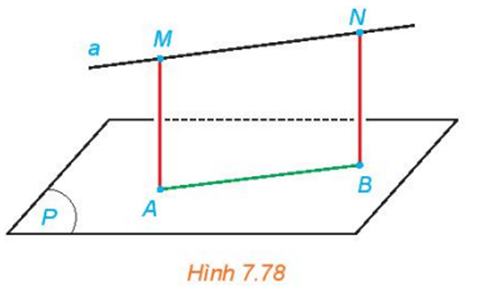
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).

Lời giải:

Vì A, B lần lượt là các hình chiếu của M, N trên (P) nên AM $\perp$ (P), BN $\perp$ (P).

Do đó AM // BN hay A, B, M, N cùng thuộc một mặt phẳng.

Vì MN // (P) và (ABNM) $\cap$ (P) = AB nên MN // AB.

Vì AM // BN và MN // AB nên ABNM là hình bình hành.

Mặt khác AM $\perp$ (P) nên AM $\perp$ AB. Do đó ABNM là hình chữ nhật.

Vì ABNM là hình chữ nhật nên AM = BN nên M, N có cùng khoảng cách đến (P).

HĐ3 trang 56 Toán 11 Tập 2: a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?

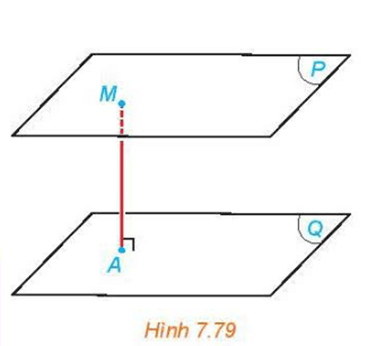
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.

Lời giải:

a) Khi M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n không thay đổi vì m // n.

b) Vì (P) // (Q) nên các đường thẳng trên mặt phẳng (P) đều song song với mặt phẳng (Q).

Khi đó M thay đổi trên (P) thì khoảng cách từ M đến (Q) không thay đổi (dựa vào kết quả của hoạt động 2).

Câu hỏi trang 56 Toán 11 Tập 2: Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P), (Q)) có mối quan hệ gì?

Lời giải:

Lấy M bất kì thuộc a nằm trong mặt phẳng (P), suy ra M thuộc (P).

Vì a // (Q), khi đó d (a, (Q)) = d(M, (Q)).

Vì (P) // (Q) nên d((P), (Q)) = d(M, (Q)).

Do đó d(a, (Q)) = d((P), (Q)).

Luyện tập 2 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA $\perp$ (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.

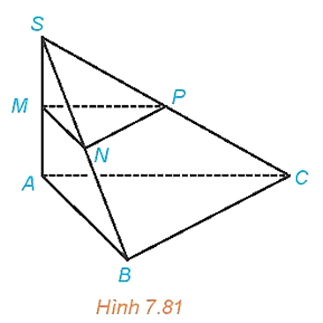
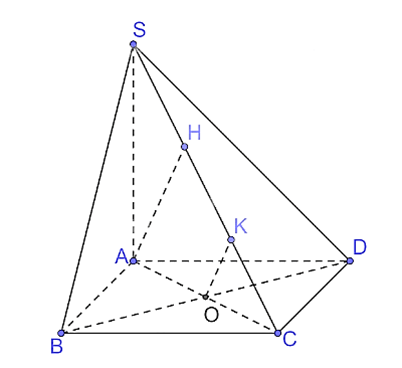
a) Tính d((MNP), (ABC)) và d(NP, (ABC)).

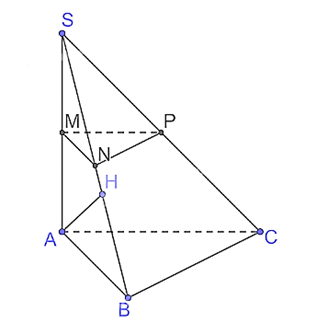
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A, (SBC)).

Lời giải:

a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB nên MN là đường trung bình của tam giác SAB suy ra MN // AB, do đó MN // (ABC).

Xét tam giác SBC có N là trung điểm của SB, P là trung điểm của SC nên PN là đường trung bình của tam giác SBC suy ra PN // BC, do đó PN // (ABC).

Vì MN // (ABC) và PN // (ABC) mà MN $\cap$ PN = N nên (MNP) // (ABC).

Khi đó d((MNP), (ABC)) = d(M, (ABC)).

Vì SA $\perp$ (ABC) nên MA $\perp$ (ABC). Do đó d(M, (ABC)) = MA.

Vì M là trung điểm SA nên AM = $\frac{SA}{2}=\frac{h}{2}$ .

Do đó d((MNP), (ABC)) = $\frac{h}{2}$ .

Vì PN // (ABC) nên d(NP, (ABC)) = d(N, (ABC)).

Vì MN // (ABC) nên d(N, (ABC)) = d(M, (ABC)) = MA = $\frac{h}{2}$ .

Vậy d(NP, (ABC)) = $\frac{h}{2}$ .

b) Vì ABC là tam giác vuông tại B nên BC $\perp$ AB.

Vì SA $\perp$ (ABC) nên SA $\perp$ BC mà BC $\perp$ AB nên BC $\perp$ (SAB), suy ra (SBC) $\perp$ (SAB).

Kẻ AH $\perp$ SB tại H.

Vì 

Khi đó d(A, (SBC)) = AH.

Vì SA $\perp$ (ABC) nên SA $\perp$ AB.

Xét tam giác SAB vuông tại A, AH là đường cao, có

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{B}^2}=\frac{1}{h^2}+\frac{1}{a^2}=\frac{a^2+h^2}{a^2{h}^2}$$\Rightarrow AH=\frac{ah}{\sqrt{a^2+h^2}}$.

Vậy d(A, (SBC)) = $\frac{ah}{\sqrt{a^2+h^2}}$ .

Vận dụng 1 trang 57 Toán 11 Tập 2: Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 15° so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?

Lời giải:

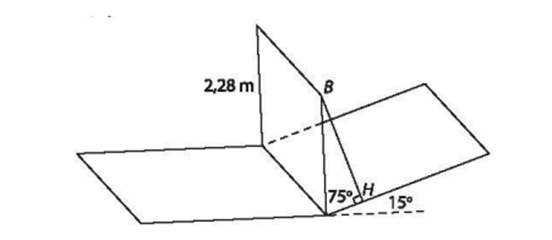
Gọi B là một điểm nằm trên thanh ngang và H là hình chiếu vuông góc xuống mặt dốc.

Vì dốc nghiêng 15° so với phương ngang nên góc giữa cột và mặt phẳng dốc bằng 75°.

Khi đó khoảng cách từ B đến mặt phẳng dốc là BH = 2,28 . sin75°$\approx$ 2,2 (m).

Do đó không cho phép xe cao 2,21 m đi qua.

3. Khoảng cách giữa hai đường thẳng chéo nhau

HĐ4 trang 57 Toán 11 Tập 2: Cho hai đường thẳng chéo nhau a và b. Gọi (Q) là mặt phẳng chứa đường thẳng b và song song với a. Hình chiếu a' của a trên (Q) cắt b tại N. Gọi M là hình chiếu của N trên a (H.7.83).

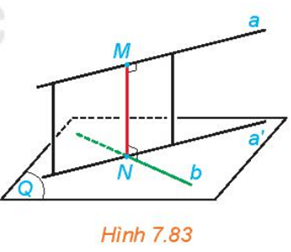
a) Mặt phẳng chứa a và a' có vuông góc với (Q) hay không?

b) Đường thẳng MN có vuông góc với cả hai đường thẳng a và b hay không?

c) Nêu mối quan hệ của khoảng cách giữa a, (Q) và độ dài đoạn thẳng MN.

Lời giải:

a) Vì a' là hình chiếu của a trên (Q) nên a và a' thuộc cùng một mặt phẳng. Hơn nữa, mặt phẳng đó chứa phương chiếu là đường thẳng vuông góc với (Q) nên mặt phẳng chứa a và a' vuông góc với (Q).

b) Gọi mặt phẳng chứa a và a' là mặt phẳng (P).

Vì a // (Q) và (P) $\cap$ (Q) = a' nên a // a'.

Vì MN $\perp$ a nên MN $\perp$ a'.

Trong mặt phẳng (P) có MN và phương chiếu vuông góc lên (Q) cùng vuông góc với a nên chúng song song với nhau. Do đó MN $\perp$ (Q) nên MN $\perp$ b.

c) Vì a // (Q) nên d(a, (Q)) = d(M, (Q)) = MN (vì MN $\perp$ (Q)).

Khám phá trang 58 Toán 11 Tập 2: Cho đường thẳng a vuông góc với mặt phẳng (P) và cắt (P) tại O. Cho đường thẳng b thuộc mặt phẳng (P). Hãy tìm mối quan hệ giữa khoảng cách giữa a, b và khoảng cách từ Ođến b (H.7.88).

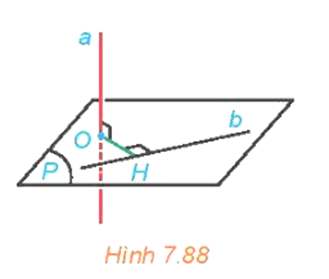
Lời giải:

Ta có d(O, b) = OH.

Vì a $\perp$ (P) nên a $\perp$ OH mà OH $\perp$ b nên OH là đoạn vuông góc chung của a và b, do đó d(a, b) = OH.

Vậy d(a, b) = d(O, b).

Luyện tập 3 trang 58 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA $\perp$ (ABCD), SA = a$\sqrt{2}$.

a) Tính khoảng cách từ A đến SC.

b) Chứng minh rằng BD $\perp$ (SAC).

c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.

Lời giải:

a) Hạ AH $\perp$ SC tại H. Khi đó d(A, SC) = AH.

Xét tam giác ABC vuông tại B, có AC = $\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Vì SA $\perp$ (ABCD) nên SA $\perp$ AC.

Xét tam giác SAC vuông tại A, AH là đường cao, ta có:

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{C}^2}$$=\frac{1}{2a^2}+\frac{1}{2a^2}=\frac{1}{a^2}$⇒ AH = a.

Vậy d(A, SC) = a.

b) Do ABCD là hình vuông nên AC $\perp$ BD.

Vì SA $\perp$ (ABCD) nên SA $\perp$ BD mà AC $\perp$ BD nên BD $\perp$ (SAC).

c) Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD.

Kẻ OK $\perp$ SC tại K.

Vì BD $\perp$ (SAC) nên BD $\perp$ OK mà OK $\perp$ SC nên OK là đường vuông góc chung của BD và SC.

Xét tam giác CHA có O là trung điểm của AC và OK // AH (vì cùng vuông góc với SC) nên K là trung điểm của CH. Do đó OK là đường trung bình của tam giác CHA nên OK = $\frac{AH}{2}=\frac{a}{2}$ .

Vậy d(BD, SC) = $\frac{a}{2}$ .

Thảo luận trang 58 Toán 11 Tập 2: Khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia. Hãy thảo luận để làm rõ nhận xét này.

Lời giải:

- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.

- Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên mặt phẳng (P).

- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm M bất kì trên a đến mặt phẳng (P).

- Khoảng cách giữa hai mặt phẳng song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.

Mà đường vuông góc là đường ngắn nhất nên khoảng cách giữa hai hình được nêu trong bài học (điểm, đường thẳng, mặt phẳng) là khoảng cách nhỏ nhất giữa một điểm thuộc hình này và một điểm thuộc hình kia.

Bài tập

Bài 7.22 trang 59 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là một hình vuông cạnh a, mặt bên SAD là một tam giác đều và (SAD) $\perp$ (ABCD).

a) Tính chiều cao của hình chóp.

b) Tính khoảng cách giữa BC và (SAD).

c) Xác định đường vuông góc chung và tính khoảng cách giữa AB và SD.

Lời giải:

a) Kẻ SE $\perp$ AD tại E.

Vì (SAD) $\perp$ (ABCD), (SAD) $\cap$ (ABCD) = AD mà SE $\perp$ AD nên SE $\perp$ (ABCD).

Vì tam giác SAD là tam giác đều cạnh a nên SE = $\frac{a\sqrt{3}}{2}$ .

Vậy chiều cao của hình chóp bằng $\frac{a\sqrt{3}}{2}$ .

b) Vì ABCD là hình vuông nên BC // AD, suy ra BC // (SAD).

Khi đó d(BC, (SAD)) = d(B, (SAD)).

Vì ABCD là hình vuông nên AB $\perp$ AD mà SE $\perp$ (ABCD) nên SE $\perp$ AB.

Vì AB $\perp$ AD và SE $\perp$ AB nên AB $\perp$ (SAD).

Do đó d(BC, (SAD)) = d(B, (SAD)) = AB = a.

c) Kẻ AF $\perp$ SD tại F, mà AB $\perp$ (SAD) nên AB $\perp$ AF.

Vì AF $\perp$ SD và AB $\perp$ AF nên AF là đường vuông góc chung của AB và SD.

Vì tam giác SAD đều có AF là đường cao nên AF = $\frac{a\sqrt{3}}{2}$.

Vậy d(AB, SD) = AF = $\frac{a\sqrt{3}}{2}$ .

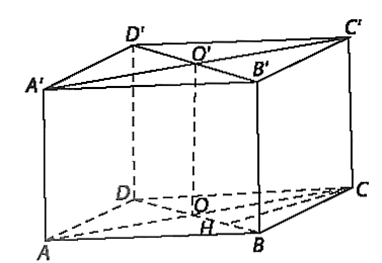
Bài 7.23 trang 59 Toán 11 Tập 2: Cho hình hộp chữ nhật ABCD.A'B'C'D'có AA' = a, AB = b, BC = c.

a) Tính khoảng cách giữa CC' và (BB'D'D).

b) Xác định đường vuông góc chung và tính khoảng cách giữa AC và B'D'.

Lời giải:

a) Kẻ CH $\perp$ BD tại H.

Vì BB' $\perp$ (ABCD) nên BB' $\perp$ CH mà CH $\perp$ BD nên CH $\perp$ (BB'D'D).

Vì BB'C'C là hình chữ nhật nên BB' // CC' nên CC' // (BB'D'D).

Khi đó d(CC', (BB'D'D)) = d(C, (BB'D'D)) = CH.

Vì ABCD là hình chữ nhật nên AB = CD = b; AD = BC = c.

Xét tam giác BCD vuông tại C, CH là đường cao nên

$\frac{1}{C{H}^2}=\frac{1}{B{C}^2}+\frac{1}{C{D}^2}$$=\frac{1}{c^2}+\frac{1}{b^2}=\frac{b^2+c^2}{b^2{c}^2}$$\Rightarrow CH=\frac{bc}{\sqrt{b^2+c^2}}$.

Vậy d(CC', (BB'D'D)) $=\frac{bc}{\sqrt{b^2+c^2}}$ .

b) Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D'.

Do ABCD là hình chữ nhật nên O là trung điểm của AC, BD và A'B'C'D' là hình chữ nhật nên O' là trung điểm của A'C' và B'D'.

Có AA' // CC' và AA' = CC' (do chúng cùng song song và bằng BB’) nên AA'C'C là hình bình hành mà AA' $\perp$ (ABCD) nên AA' $\perp$ AC. Do đó AA'C'C là hình chữ nhật.

Do AA'C'C là hình chữ nhật và O là trung điểm của AC, O' là trung điểm của A'C' nên OO' $\perp$ AC và OO' = AA' = a.

Có BB' // DD' và BB' = DD' (do chúng cùng song song và bằng AA') nên BB'D'D là hình bình hành mà BB' $\perp$ (ABCD) nên BB' $\perp$ BD. Do đó BB'D'D là hình chữ nhật.

Vì BB'D'D là hình chữ nhật và O là trung điểm của BD, O' là trung điểm của B'D' nên OO' $\perp$ B'D'.

Vì OO' $\perp$ AC và OO' $\perp$ B'D' nên OO' là đường vuông góc chung của AC và B'D'.

Khi đó d(AC, B'D') = OO' = a.

Bài 7.24 trang 59 Toán 11 Tập 2: Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:

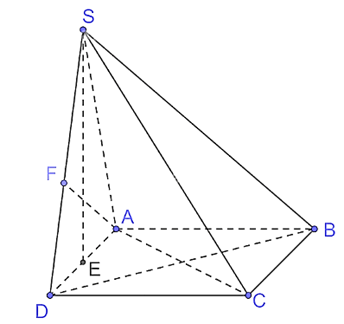
a) MN là đường vuông góc chung của AB và CD.

b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.

Lời giải:

a) Xét tam giác ADB có AD = BD = a nên tam giác ADB cân tại D.

Vì M là trung điểm của AB nên DM là trung tuyến.

Vì tam giác ADB cân tại D, DM là trung tuyến nên DM đồng thời là đường cao hay DM $\perp$ AB.

Xét tam giác ABC có AC = BC = a nên tam giác ABC cân tại C mà CM là trung tuyến nên CM là đường cao hay CM $\perp$ AB.

Vì DM $\perp$ AB và CM $\perp$ AB nên AB $\perp$ (DCM), suy ra AB $\perp$ MN.

Xét tam giác ADC có AD = AC = a nên tam giác ACD cân tại A mà AN là trung tuyến nên AN đồng thời là đường cao hay AN $\perp$ CD.

Xét tam giác BCD có BD = BC = a nên tam giác BCD cân tại B mà BN là trung tuyến nên BN đồng thời là đường cao hay BN $\perp$ CD.

Vì AN $\perp$ CD và BN $\perp$ CD nên CD $\perp$ (ABN), suy ra CD $\perp$ MN.

Vì AB $\perp$ MN và CD $\perp$ MN nên MN là đường vuông góc chung của AB và CD.

b) Vì AB $\perp$ (DCM) nên AB $\perp$ CD.

Gọi E là trung điểm của BC.

Xét tam giác ABC có AB = AC = a nên tam giác ABC cân tại A mà AE là trung tuyến nên AE đồng thời là đường cao hay AE $\perp$ BC.

Xét tam giác BDC có BD = CD = a nên tam giác BCD cân tại D mà DE là trung tuyến nên DE đồng thời là đường cao hay DE $\perp$ BC.

Có AE $\perp$ BC và DE $\perp$ BC nên BC $\perp$ (ADE), suy ra BC $\perp$ AD.

Gọi F là trung điểm của BD.

Xét tam giác ADB có AB = AD = a nên tam giác ADB cân tại A mà AF là trung tuyến nên AF đồng thời là đường cao hay AF $\perp$ BD.

Xét tam giác BCD có BC = CD = a nên tam giác BCD cân tại C mà CF là trung tuyến nên CF đồng thời là đường cao hay CF $\perp$ BD.

Vì AF $\perp$ BD và CF $\perp$ BD nên BD $\perp$ (ACF), suy ra BD $\perp$ AC.

Bài 7.25 trang 59 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D'có cạnh a.

a) Chứng minh rằng hai mặt phẳng (D'AC)và (BC'A') song song với nhau và DB' vuông góc với hai mặt phẳng đó.

b) Xác định các giao điểm E, F của DB' với (D'AC), (BC'A'). Tính d((D'AC), (BC'A')).

Lời giải:

a) Vì AA' // CC' và AA' = CC' (do chúng cùng song song và bằng BB') nên AA'C'C là hình bình hành, suy ra AC // A'C' do đó A'C' // (D'AC).

Vì AB // C'D' và AB = C'D' (do chúng cùng song song và bằng CD) nên ABC'D' là hình bình hành suy ra BC' // AD', do đó BC' // (D'AC).

Vì A'C' // (D'AC) và BC' // (D'AC) nên (BC'A') // (D'AC).

Vì ABCD là hình vuông nên AC $\perp$ BD.

Vì BB' $\perp$ (ABCD) nên BB' $\perp$ AC mà AC $\perp$ BD nên AC $\perp$ (BB'D), suy ra AC $\perp$ DB'.

Vì AC // A'C' mà AC $\perp$ DB' nên A'C' $\perp$ DB'.

Do AD $\perp$ (ABB'A') nên AD $\perp$ A'B.

Vì ABB'A' là hình vuông nên AB' $\perp$ A'B mà AD $\perp$ A'B nên A'B $\perp$ (ADB').

Suy ra A'B $\perp$ DB'.

Có A'C' $\perp$ DB' và A'B $\perp$ DB' nên DB' $\perp$ (BC'A').

Vì A'D' // BC và A'D' = BC (do chúng cùng song song và bằng AD) nên A'D'CB là hình bình hành, suy ra A'B // D'C mà A'B $\perp$ DB' nên D'C $\perp$ DB'.

Có AC $\perp$ DB' và D'C $\perp$ DB' nên DB' $\perp$ (D'AC).

b) Gọi O và O' lần lượt là tâm của hai hình vuông ABCD và A'B'C'D'.

Trong mặt phẳng (BDD'B'), có DB' $\cap$ D'O = E. Khi đó DB' $\cap$ (D'AC) = E.

Trong mặt phẳng (BDD'B'), có DB' $\cap$ BO' = F. Khi đó DB' $\cap$ (BC'A') = F.

Vì (BC'A') // (D'AC) nên d((D'AC), (BC'A')) = d(E, (BC'A')) = EF (vì DB' $\perp$ (BC'A')).

Vì DB' $\perp$ (BC'A') nên DB' $\perp$ BO' và DB' $\perp$ (D'AC) nên DB' $\perp$ D'O, suy ra BO' // D'O.

Xét tam giác DBF, có OE // BF nên theo định lí Ta lét, ta có: $\frac{DE}{EF}=\frac{DO}{OB}=1$$\Rightarrow DE=EF$ .

Xét tam giác B'D'E có O'F // D'E nên theo định lí Ta lét, ta có: $\frac{B^{\text{'}}F}{EF}=\frac{B^{\text{'}}{O}^{\text{'}}}{O^{\text{'}}{D}^{\text{'}}}=1$$\Rightarrow$B'F = EF.

Do đó B'F = EF = DE $\Rightarrow$EF = $\frac{1}{3}$DB' .

Xét tam giác BCD vuông tại C, có $B{D}^2=B{C}^2+C{D}^2=a^2+a^2=2a^2$.

Xét tam giác B'BD vuông tại B, có $B^{\text{'}}{D}^2=B^{\text{'}}{B}^2+B{D}^2=a^2+2a^2=3a^2$

$\Rightarrow B^{\text{'}}D=a\sqrt{3}$$\Rightarrow EF=\frac{a\sqrt{3}}{3}$

Vậy d((D'AC), (BC'A')) = $\frac{a\sqrt{3}}{3}$ .

Bài 7.26 trang 59 Toán 11 Tập 2: Giá đỡ ba chân ở Hình 7.90 đang được mở sao cho ba gốc chân cách đều nhau một khoảng cách bằng 110 cm. Tính chiều cao của giá đõ, biết các chân của giá đỡ dài 129 cm.

Lời giải:

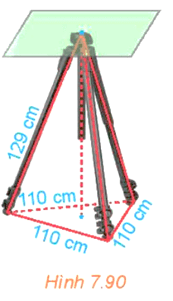
Giá đỡ ba chân ở Hình 7.90 có dạng hình chóp đều S.ABC.

Vì S.ABC là hình chóp đều nên SH $\perp$ (ABC) với H là trọng tâm của tam giác ABC.

Gọi AH $\cap$ BC tại M. Khi đó M là trung điểm của BC.

Vì ABC là tam giác đều cạnh 110 cm, AM là đường cao nên AM = $\frac{110\sqrt{3}}{2}$ (cm).

Vì AH = $\frac{2}{3}$AM = $\frac{110\sqrt{3}}{2}$ (cm).

Xét tam giác SHA vuông tại H, có:

SH = $\sqrt{S{A}^2-A{H}^2}$$=\sqrt{{129}^2-{\left(\frac{110\sqrt{3}}{3}\right)}^2}$$=\sqrt{\frac{37823}{3}}\approx 112,28$ (cm).

Vậy chiều cao giá đỡ khoảng 112,28 cm.

Bài 7.27 trang 59 Toán 11 Tập 2: Một bể nước có đáy thuộc mặt phẳng nằm ngang. Trong trường hợp này, độ sâu của bể là khoảng cách giữa mặt nước và đáy bể. Giải thích vì sao để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi nằm trong bể nước.

Lời giải:

Giả sử mặt phẳng đáy bể nước là mặt phẳng (P), mặt phẳng mặt nước là mặt phẳng (Q), dây dọi là đường thẳng MH.

Khi đó ta có (P) // (Q). Mà d((P), (Q)) = d(M, (P)), với M $\in$ (Q).

Lại có, sợi dây của quả dọi có phương vuông góc với mặt phẳng nước và đáy bể, do đó MH $\perp$ (P).

Khi đó d(M, (P)) = MH, MH chính là độ dài đoạn dây dọi nằm trong bể nước.

Vậy để đo độ sâu của bể, ta có thể thả quả dọi chạm đáy bể và đo chiều dài của đoạn dây dọi nằm trong bể nước.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác: