Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với (ABCD), SA = a căn 2

Luyện tập 3 trang 58 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA $\perp$ (ABCD), SA = a$\sqrt{2}$.

a) Tính khoảng cách từ A đến SC.

b) Chứng minh rằng BD $\perp$ (SAC).

c) Xác định đường vuông góc chung và tính khoảng cách giữa BD và SC.

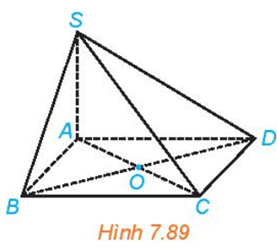
Trả lời

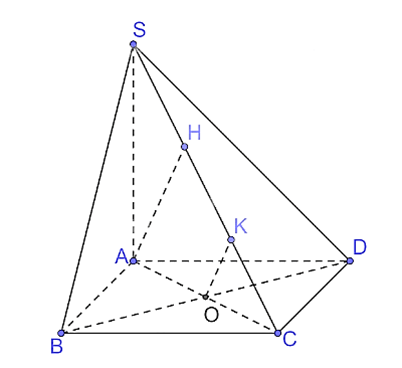
a) Hạ AH $\perp$ SC tại H. Khi đó d(A, SC) = AH.

Xét tam giác ABC vuông tại B, có AC = $\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$.

Vì SA $\perp$ (ABCD) nên SA $\perp$ AC.

Xét tam giác SAC vuông tại A, AH là đường cao, ta có:

$\frac{1}{A{H}^2}=\frac{1}{S{A}^2}+\frac{1}{A{C}^2}$$=\frac{1}{2a^2}+\frac{1}{2a^2}=\frac{1}{a^2}$⇒ AH = a.

Vậy d(A, SC) = a.

b) Do ABCD là hình vuông nên AC $\perp$ BD.

Vì SA $\perp$ (ABCD) nên SA $\perp$ BD mà AC $\perp$ BD nên BD $\perp$ (SAC).

c) Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD.

Kẻ OK $\perp$ SC tại K.

Vì BD $\perp$ (SAC) nên BD $\perp$ OK mà OK $\perp$ SC nên OK là đường vuông góc chung của BD và SC.

Xét tam giác CHA có O là trung điểm của AC và OK // AH (vì cùng vuông góc với SC) nên K là trung điểm của CH. Do đó OK là đường trung bình của tam giác CHA nên OK = $\frac{AH}{2}=\frac{a}{2}$ .

Vậy d(BD, SC) = $\frac{a}{2}$ .

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: