Bài 7.24 trang 59 Toán 11 Tập 2: Cho tứ diện ABCD có các cạnh đều bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh rằng:
a) MN là đường vuông góc chung của AB và CD.
b) Các cặp cạnh đối diện trong tứ diện ABCD đều vuông góc với nhau.
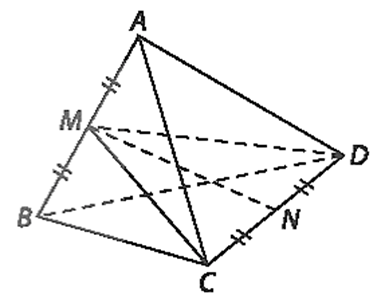
a) Xét tam giác ADB có AD = BD = a nên tam giác ADB cân tại D.
Vì M là trung điểm của AB nên DM là trung tuyến.
Vì tam giác ADB cân tại D, DM là trung tuyến nên DM đồng thời là đường cao hay DM AB.
Xét tam giác ABC có AC = BC = a nên tam giác ABC cân tại C mà CM là trung tuyến nên CM là đường cao hay CM AB.
Vì DM AB và CM AB nên AB (DCM), suy ra AB MN.
Xét tam giác ADC có AD = AC = a nên tam giác ACD cân tại A mà AN là trung tuyến nên AN đồng thời là đường cao hay AN CD.
Xét tam giác BCD có BD = BC = a nên tam giác BCD cân tại B mà BN là trung tuyến nên BN đồng thời là đường cao hay BN CD.
Vì AN CD và BN CD nên CD (ABN), suy ra CD MN.
Vì AB MN và CD MN nên MN là đường vuông góc chung của AB và CD.
b) Vì AB (DCM) nên AB CD.
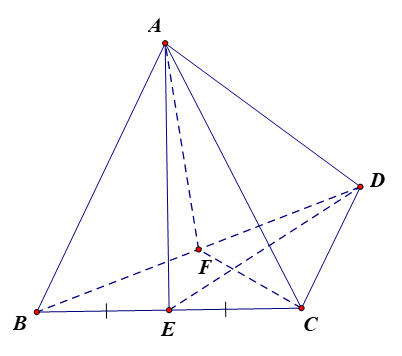
Gọi E là trung điểm của BC.
Xét tam giác ABC có AB = AC = a nên tam giác ABC cân tại A mà AE là trung tuyến nên AE đồng thời là đường cao hay AE BC.
Xét tam giác BDC có BD = CD = a nên tam giác BCD cân tại D mà DE là trung tuyến nên DE đồng thời là đường cao hay DE BC.
Có AE BC và DE BC nên BC (ADE), suy ra BC AD.
Gọi F là trung điểm của BD.
Xét tam giác ADB có AB = AD = a nên tam giác ADB cân tại A mà AF là trung tuyến nên AF đồng thời là đường cao hay AF BD.
Xét tam giác BCD có BC = CD = a nên tam giác BCD cân tại C mà CF là trung tuyến nên CF đồng thời là đường cao hay CF BD.
Vì AF BD và CF BD nên BD (ACF), suy ra BD AC.
Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: