Cho tam giác đều ABC có cạnh bằng a. Tính độ dài các vectơ AB - Ac và AB + AC.

Bài 4.8 trang 54 Toán 10 Tập 1: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài các vectơ AB - Ac và AB + AC.

Trả lời

Ta có: $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ (quy tắc hiệu)

Suy ra $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=CB=a.$ 

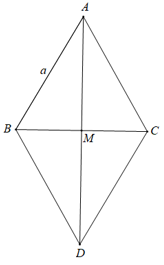
Gọi D là điểm thoả mãn điều kiện ABDC là hình hình hành.

 $\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$ (quy tắc hình bình hành)

$\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=AD$

Gọi M là giao điểm của AD và BC

⇒ M là trung điểm của BC và AD (tính chất hình bình hành)

AM vừa là đường trung tuyến vừa là đường cao của tam giác đều ABC.

Do đó tam giác ABM vuông tại M có AB = a, BM = $\frac{1}{2}BC=\frac{1}{2}a$, áp dụng định lí Pythagore ta có: AB² = AM² + BM²

⇒ AM² = AB² – BM² = $a^2-{\left(\frac{1}{2}a\right)}^2=a^2-\frac{1}{4}{a}^2=\frac{3a^2}{4}$

$\Rightarrow AM=\frac{a\sqrt{3}}{2}$
Mà M là trung điểm của AD nên AD = 2AM $=2.\frac{a\sqrt{3}}{2}=a\sqrt{3}$

$\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=AD=a\sqrt{3}$

Vậy $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=a$ và $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}$

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto