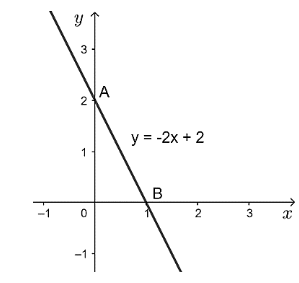Giải SBT Toán 8 (Kết nối tri thức) Bài tập ôn tập cuối năm

Sách bài tập Toán lớp 8 Bài tập ôn tập cuối năm

Đại số

Bài tập 1 trang 81 SBT Toán lớp 8 Tập 2: Biết rằng hai đa thức A và B thỏa mãn các điều kiện sau:

A . (– 0,5x²y) = – 6x²y³ + x³y² + 3x²y + 3x²y – 2x⁴y.

A + B = 9y² + 4x² – 6.

a) Tìm các đa thức A và B, xác định bậc của mỗi đa thức đó.

b) Tìm giá trị của B tại x = 3; y = 2.

Lời giải:

a) Vì A . (– 0,5x²y) = – 6x²y³ + x³y² + 3x²y + 3x²y – 2x⁴y

Suy ra A = (– 6x²y³ + x³y² + 3x²y – 2x⁴y) : (–0,5x²y)

          = – 6x²y³ : (–0,5x²y) + x³y² : (–0,5x²y) + 3x²y : (–0,5x²y) – 2x⁴y : (–0,5x²y)

= 12y² – 2xy – 6 + 4x².

Vậy A là đa thức bậc hai.

Ta có A + B = 9y² + 4x² – 6

Suy ra B = (9y² + 4x² – 6) – A

= (9y² + 4x² – 6) – (12y² – 2xy – 6 + 4x²)

= 9y² + 4x² – 6 – 12y² + 2xy + 6 – 4x²

= (9y² – 12y²) + (4x² – 4x²) + 2xy + (6 – 6)

= –3y² + 2xy.

Vậy B là đa thức bậc hai.

b) Với x = 3, y = 2 thay vào đa thức B ta được:

B = –3 . 2² + 2 . 3 . 2 = – 12 + 12 = 0.

Vậy giá trị của B tại x = 3; y = 2 là 0.

Bài tập 2 trang 81 SBT Toán lớp 8 Tập 2: Cho các đa thức:

A = 27x³y⁶ –  $\frac{1}{8}$y³;           B = 9x²y⁴ +  $\frac{3}{2}$xy³ + $\frac{1}{4}$y²;        C = 3xy² – $\frac{1}{2}$y.

Chứng minh rằng A : B = C

Lời giải:

Ta có B . C = $\left(9x^2{y}^4+\frac{3}{2}x{y}^3+\frac{1}{4}{y}^2\right).\left(3x{y}^2-\frac{1}{2}y\right)$

= $9x^2{y}^4.\left(3x{y}^2-\frac{1}{2}y\right)+\frac{3}{2}x{y}^3.\left(3x{y}^2-\frac{1}{2}y\right)+\frac{1}{4}{y}^2.\left(3x{y}^2-\frac{1}{2}y\right)$

= 27x³y⁶ – $\frac{9}{2}{x}^2{y}^5$ + $\frac{9}{2}{x}^2{y}^5$ - $\frac{3}{4}x{y}^4$ + $\frac{3}{4}x{y}^4$ - $\frac{1}{8}{y}^3$

= 27x³y⁶ – $\frac{1}{8}$y3 = A

Do đó, B . C = A. Suy ra A : B = C (đcpcm).

Bài tập 3 trang 81 SBT Toán lớp 8 Tập 2: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

M = (3x – 2)² – (3x + 2)² + (x + 2)³ + (x – 2)³ – 2x³.

Lời giải:

Ta có:

M = (3x – 2)² – (3x + 2)² + (x + 2)³ + (x – 2)³ – 2x³

= (9x² – 12x + 4) – (9x² + 12x + 4) + (x³ + 6x² + 12x + 8) + (x³ – 6x² + 12x – 8) – 2x³

= 9x² – 12x + 4 – 9x² – 12x – 4 + x³ + 6x² + 12x + 8 + x³ – 6x² + 12x – 8 – 2x³

= (9x² – 9x² + 6x² – 6x²) – (12x – 12x – 12x + 12x) + (x³ + x³ – 2x³) + (4 – 4 + 8 – 8)

= 0.

Do đó, giá trị của biểu thức M không phụ thuộc vào giá trị của biến x.

Bài tập 4 trang 81 SBT Toán lớp 8 Tập 2: Phân tích các đa thức sau thành nhân tử:

a) x³ + y³ + 5x + 5y;

b) 16x² + 8xy + y² – 4x².

Lời giải:

a)

x³ + y³ + 5x + 5y

= (x³ + y³) + (5x + 5y)

= (x + y)(x² – xy + y²) + 5(x + y)

= (x + y)(x² – xy + y² + 5).

b)

16x² + 8xy + y² – 4x²

= (16x² + 8xy + y²) – (4x²)

= (4x + y)² – (2x)²

= (4x + y – 2x)(4x + y + 2x)

= (2x + y)(6x + y).

Bài tập 5 trang 81 SBT Toán lớp 8 Tập 2: Thực hiện các phép tính sau:

a) $\frac{2x+4}{x+3}+\frac{3}{x}-\frac{6}{x^2+3x}$ ;

b) $\frac{x^2-3x+4}{x^2+x}:\frac{x^2-x-12}{x^2-x}$.

Chú ý: Đề câu b) trong sách chưa chính xác, cần sửa thành $\frac{x^2-3x-4}{x^2+x}:\frac{x^2-x-12}{x^2-x}$.

Lời giải:

a) $\frac{2x+4}{x+3}+\frac{3}{x}-\frac{6}{x^2+3x}$

$=\frac{x\left(2x+4\right)}{x\left(x+3\right)}+\frac{3\left(x+3\right)}{x\left(x+3\right)}-\frac{6}{x\left(x+3\right)}$

$=\frac{\left(2x^2+4x\right)+\left(3x+9\right)-6}{x\left(x+3\right)}$

$=\frac{2x^2+7x\text{\hspace{0.17em}}+3}{x(x+3)}$

$=\frac{\left(2x^2+6x\right)+\left(x\text{\hspace{0.17em}}+3\right)}{x(x+3)}$

$=\frac{2x(x+3)+(x+3)}{x(x+3)}$

$=\frac{(x+3)(2x+1)}{x(x+3)}$

$=\frac{2x+1}{x}$

b, $\frac{x^2-3x-4}{x^2+x}:\frac{x^2-x-12}{x^2-x}$

$=\frac{x^2+x-4x-4}{x\left(x+1\right)}:\frac{x^2-4x+3x-12}{x\left(x-1\right)}$

$=\frac{x\left(x+1\right)-4\left(x+1\right)}{x\left(x+1\right)}:\frac{x\left(x-4\right)+3\left(x-4\right)}{x\left(x-1\right)}$

$=\frac{\left(x-4\right)\left(x+1\right)}{x\left(x+1\right)}:\frac{\left(x+3\right)\left(x-4\right)}{x\left(x-1\right)}$

$=\frac{\left(x-4\right)\left(x+1\right)}{x\left(x+1\right)}\cdot \frac{x\left(x-1\right)}{\left(x+3\right)\left(x-4\right)}$

$=\frac{x-1}{x+3}$

Bài tập 6 trang 81 SBT Toán lớp 8 Tập 2: Cho phân thức đại số $P=\frac{x^3+8}{x^2-4}$.

a) Tìm điều kiện xác định của phân thức.

b) Rút gọn phân thức đã cho.

c) Sử dụng kết quả câu b), tìm tất cả các số nguyên x sao cho giá trị của phân thức P đã cho là số nguyên.

Lời giải:

a) Điều kiện xác định của phân thức P là: x² – 4 ≠ 0, hay x² ≠ 4, tức là x ≠ ± 2.

b) Với điều kiện xác định trên, ta có:

$P=\frac{x^3+8}{x^2-4}=\frac{\left(x+2\right)\left(x^2-2x+4\right)}{\left(x-2\right)\left(x+2\right)}=\frac{x^2-2x+4}{x-2}$

$=\frac{x\left(x-2\right)+4}{x-2}=x+\frac{4}{x-2}$

c) Ta có: $P=x+\frac{4}{x-2}$

Vì x nguyên, để P có giá trị nguyên thì $\frac{4}{x-2}$ phải có giá trị là số nguyên. Khi đó, x – 2 là ước nguyên của 4. Do đó, x – 2 ∈ {±1; ±2; ±4}.

Ta có bảng sau:

x – 2	1	–1	2	–2	4	–4
x	3	1	4	0	6	–2

Kết hợp với điều kiện của x ta thấy x = – 2 không thỏa mãn, với các giá trị còn lại của x, thay vào P ta thấy đều thỏa mãn. 

Vậy x ∈ {3; 1; 4; 0; 6}.

Bài tập 7 trang 81 SBT Toán lớp 8 Tập 2: Quãng đường AC gồm hai đoạn AB và BC. Đoạn BC dài hơn đoạn AB là 60 km. Một ô tô đi từ A đến B với vận tốc 50 km/h, rồi tiếp tục đi từ B đến C với vận tốc 60 km/h. Tính quãng đường AC biết thời gian đi trên đoạn đường AB ít hơn thời gian đi trên đoạn đường BC là 1 giờ 30 phút.

Chú ý: Đề bài trong Sách sai, cần sửa lại đề như sau:

Quãng đường AC gồm hai đoạn AB và BC. Đoạn BC dài hơn đoạn AB là 60 km. Một ô tô đi từ A đến B với vận tốc 60 km/h, rồi tiếp tục đi từ B đến C với vận tốc 50 km/h. Tính quãng đường AC biết thời gian đi trên đoạn đường AB ít hơn thời gian đi trên đoạn đường BC là 1 giờ 30 phút.

Lời giải:

Gọi x (km) là chiều dài quãng đường AB. Điều kiện: x > 0.

Khi đó, chiều dài quãng đường BC là: x + 60 (km).

Thời gian đi trên quãng đường AB là: $\frac{x}{60}$ (giờ).

Thời gian đi trên quãng đường BC là:$\frac{x+60}{50}$ (giờ).

Vì thời gian đi trên đoạn đường AB ít hơn thời gian đi trên đoạn đường BC là 1 giờ 30 phút hay $\frac{3}{2}$ giờ nên ta có phương trình:

$\frac{x+60}{50}-\frac{x}{60}=\frac{3}{2}$.

Giải phương trình trên, ta có

$\frac{x+60}{50}-\frac{x}{60}=\frac{3}{2}$

$\frac{6\left(x+60\right)}{300}-\frac{5x}{300}=\frac{450}{300}$

6x + 360 – 5x = 450 

x = 90 (thỏa mãn)

Do đó, chiều dài quãng đường AB là 90 km, chiều dài quãng đường BC là

90 + 60 = 150 (km).

Vậy chiều dài quãng đường AC là 90 + 150 = 240 (km).

Bài tập 8 trang 81 SBT Toán lớp 8 Tập 2: Cho hàm số y = (3m + 1)x – 2m.

a) Tìm điều kiện của m để hàm số đã cho là hàm số bậc nhất.

b) Tìm m để đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5.

c) Với m tìm được ở câu b), hãy vẽ đồ thị của hàm số đã cho.

Lời giải:

a) Hàm số y = (3m + 1)x – 2m là hàm số bậc nhất khi 3m + 1 ≠ 0, tức là m ≠ $\frac{-1}{3}$.

b) Vì đồ thị hàm số đã cho là đường thẳng song song với đường thẳng y = –2x + 5 nên

3m + 1 = –2 và –2m ≠ 5.

Tức là m = –1 và m ≠ $\frac{-5}{2}$. Suy ra m = – 1.

Vậy m = – 1.

c) Với m = –1, ta có y = –2x + 2.

Đồ thị hàm số y = –2x + 2 là đường thẳng đi qua hai điểm A(0; 2), B(1; 0) như hình dưới đây.

Hình học

Bài tập 9 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Từ M kẻ đường thẳng song song với BP, đường thẳng này cắt NP tại K.

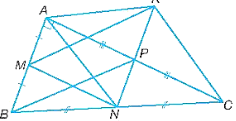
a) Tứ giác AMNP là hình gì?

b) Chứng minh tứ giác BMKP là hình bình hành.

c) Chứng minh tứ giác ANCK là hình thoi.

d) Tìm điều kiện của tam giác ABC để tứ giác ANCK là hình vuông.

Lời giải:

a) Vì tam giác ABC vuông tại A nên $\widehat{BAC}=90°$.

Vì P, N lần lượt là trung điểm của AC, BC nên PN là đường trung bình của tam giác ABC, suy ra PN // AB.

Vì M, N lần lượt là trung điểm của AB, BC nên MN là đường trung bình của tam giác ABC, suy ra MN // AC.

Xét tứ giác AMNP có:

NP // AM (do PN // AB),

NM // AP (do MN // AC).

Do đó, tứ giác AMNP là hình bình hành.

Mà $\widehat{PAM}=90°$ (do $\widehat{BAC}=90°$) nên tứ giác AMNP là hình chữ nhật.

b) Tứ giác BMKP có:

BM // KP (do PN // AB),

BP // KM (gt).

Nên tứ giác BMKP là hình bình hành.

c) Ta có $PN=\frac{1}{2}AB=AM=MB$ (do PN là đường trung bình của tam giác ABC và M là trung điểm của AB).

Vì tứ giác BMKP là hình bình hành nên KP = MB.

Do đó, KP = PN. Suy ra P là trung điểm của KN.

Vì PN song song với AB (cmt) mà AB vuông góc với AC nên KN vuông góc với AC tại P.

Tứ giác ANCK có hai đường chéo AC và KN cắt nhau tại trung điểm P của mỗi đường nên ANCK là hình bình hành.

Mà KN vuông góc với AC tại P.

Do đó, tứ giác ANCK là hình thoi.

d) Để hình thoi ANCK là hình vuông thì AC = KN.

Mà KN = 2PN = $2\cdot \frac{1}{2}AB$ = AB.

Do đó, AC = AB. Mà tam giác ABC vuông tại A. Do đó, tam giác ABC vuông cân tại A.

Bài tập 10 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt góc hạ từ H xuống AB, AC và M là trung điểm của BC. Chứng minh rằng:

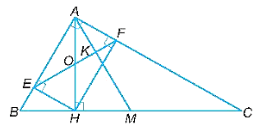
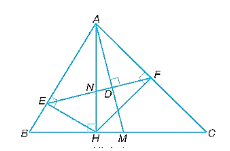
a) EF = AH.

b) AM ⊥ EF.

Lời giải:

a)Vì tam giác ABC vuông tại A nên $\widehat{BAC}=90°$.

Vì E, F lần lượt là chân các đường vuông góc hạ từ H xuống AB, AC nên HE vuông góc với AB, HF vuông góc với AC.

Do đó, $\widehat{HEB}=\widehat{HEA}=\widehat{HFA}=\widehat{HFC}=90°$.

Xét tứ giác AFHE có: $\widehat{BAC}=\widehat{HEA}=\widehat{HFA}=90°$.

Do đó, tứ giác AFHE là hình chữ nhật.

Suy ra AH = FE (hai đường chéo bằng nhau).

b) Vì tứ giác AFHE là hình chữ nhật nên $\widehat{FHE}=90°$.

Vì AM là đường trung tuyến trong tam giác ABC vuông tại A nên

AM = MB = MC = $\frac{1}{2}BC$.

Tam giác AMB có AM = MB nên tam giác AMB cân tại M.

Do đó, $\widehat{MAB}=\widehat{B}$.

Lại có $\widehat{B}=\widehat{AHE}\left(=90°-\widehat{HEB}\right)$.

Nên $\widehat{MAB}=\widehat{AHE}$ (1).

Gọi O là giao điểm của hai đường chéo FE và AH của hình chữ nhật AFHE.

Do đó, OH = OE = OF = OA.

Tam giác OAE có OA = OE nên tam giác OAE cân tại O.

Suy ra $\widehat{OEA}=\widehat{OAE}$.

Mà AE song song với FH (do AFHE là hình chữ nhật) nên $\widehat{OHF}=\widehat{OAE}$ (hai góc so le trong).

Do đó, $\widehat{OEA}=\widehat{OHF}$ (2).

Lại có $\widehat{OHF}+\widehat{OHE}=\widehat{FHE}=90°$ (3).

Từ (1), (2), (3) ta có: $\widehat{MAB}+\widehat{OEA}=90°$.

Gọi K là giao điểm của AM và EF. Khi đó, $\widehat{KAE}+\widehat{KEA}=90°$. Suy ra$\widehat{AKE}=90°$.

Vậy AM vuông góc với EF tại K.

Bài tập 11 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho $\frac{MB}{MA}=\frac{1}{3}$, N là điểm trên cạnh BC sao cho $\frac{NB}{NC}=\frac{1}{3}$.

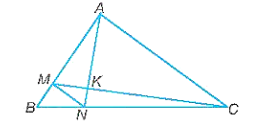
a) Chứng minh MN // AC và MN = $\frac{1}{4}$AC.

b) Gọi K là giao điểm của AN và CM. Chứng minh $\frac{KN}{KA}=\frac{KM}{KC}=\frac{1}{4}$.

c) Nếu thay điều kiện $\frac{MB}{MA}=\frac{1}{3}$ và $\frac{NB}{NC}=\frac{1}{3}$bằng điều kiện CM là phân giác của góc C, AN là phân giác của góc A thì tam giác ABC phải thỏa mãn điều kiện gì để MN // AC?

Lời giải:

a) Xét tam giác ABC có:

$\frac{MB}{MA}=\frac{NB}{NC}\left(=\frac{1}{3}\right)$

Nên MN // AC (định lí Thalès đảo).

Vì $\frac{MB}{MA}=\frac{1}{3}$ nên MA = 3MB.

Tam giác ABC có MN // AC nên $\frac{MN}{AC}=\frac{BM}{AB}=\frac{BM}{BM+MA}=\frac{BM}{4BM}=\frac{1}{4}$.

Suy ra MN = $\frac{1}{4}$AC.

b) Tam giác MNK có MN // AC nên $\frac{KN}{KA}=\frac{KM}{KC}=\frac{MN}{AC}=\frac{1}{4}$.

c) Nếu MN // AC thì $\frac{MB}{MA}=\frac{NB}{NC}$ (định lí Thalès) (1).

Vì CM là tia phân giác của góc BCA trong tam giác ABC nên $\frac{MB}{MA}=\frac{BC}{AC}$ (2).

Vì AN là tia phân giác của góc BAC trong tam giác ABC nên $\frac{NB}{NC}=\frac{AB}{AC}$ (3).

Từ (1), (2), (3) suy ra $\frac{AB}{AC}=\frac{BC}{AC}$ nên AB = BC.

Do đó, tam giác ABC cân tại B.

Ngược lại, nếu tam giác ABC cân tại B, CM là phân giác của góc C, AN là phân giác góc A thì dễ thấy MN // AC.

Vậy để MN // AC thì điều kiện là tam giác ABC cân tại B.

Bài tập 12 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:

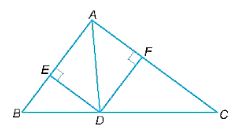
a) AE . AB = AF . AC.

b) ∆ADE ᔕ ∆AHC và ∆ANF ᔕ ∆AMB.

Lời giải:

a) Vì AH là đường cao của tam giác ABC nên$\widehat{AHB}=\widehat{AHC}=90°$.

Vì HE, HF vuông góc với AB, AC nên ta có:

$\widehat{HEB}=\widehat{HEA}=\widehat{HFA}=\widehat{HFC}=90°$.

Tam giác HEA và tam giác BHA có:

$\widehat{HEA}=\widehat{AHB}=90°$

$\widehat{BAH}$chung

Do đó, ∆HEA ᔕ ∆BHA (g.g).

Suy ra $\frac{AE}{AH}=\frac{AH}{AB}$ nên AE . AB = AH² (1).

Tam giác HFA và tam giác CHA có:

$\widehat{HFA}=\widehat{AHC}=90°$

$\widehat{CAH}$ chung

Do đó, ∆HFA ᔕ ∆CHA (g.g).

Suy ra $\frac{AF}{AH}=\frac{AH}{AC}$nên AF . AC = AH² (2).

Từ (1) và (2) suy ra AE . AB = AF . AC.

b) Vì AE . AB = AF . AC nên$\frac{AE}{AC}=\frac{AF}{AB}$.

Tam giác AEF và tam giác ACB có:

$\frac{AE}{AC}=\frac{AF}{AB}$

$\widehat{BAC}$ chung

Do đó, ∆AEF ᔕ ∆ACB (c.g.c).

Suy ra $\widehat{AEF}=\widehat{C}$.

Tam giác AED và tam giác ACH có:

$\widehat{ADE}=\widehat{AHC}=90°$

$\widehat{AEF}=\widehat{C}$ (cmt)

Do đó, ∆ADE ᔕ ∆AHC (g.g).

Suy ra $\widehat{EAD}=\widehat{CAH}$.

Do đó, $\widehat{NAF}=\widehat{CAH}=\widehat{EAD}=\widehat{MAB}$.

Hai tam giác ANF và AMB có:

$\widehat{NAF}=\widehat{MAB}$  (chứng minh trên)

$\widehat{AFN}=\widehat{AFE}=\widehat{ABC}=\widehat{ABM}$ (do ∆AEF ᔕ ∆ACB)

Do đó ∆ANF ᔕ ∆AMB (g.g).

Bài tập 13 trang 82 SBT Toán lớp 8 Tập 2:Cho tam giác ABC có AB = 3 cm, AC = 4 cm, BC = 5 cm. Lấy điểm D trên cạnh BC sao cho BD = 2 cm. Lấy các điểm E, F trên các cạnh AB, AC sao cho DE, DF lần lượt vuông góc với AB, AC.

a) Chứng minh rằng ∆BDE ᔕ ∆DCF.

b) Tính độ dài đoạn thẳng AD.

Lời giải:

a) Xét tam giác ABC có:

AB² + AC² = BC² (do 3² + 4² = 5²).

Nên tam giác ABC vuông tại A (định lí Pythagore đảo).

Ta có DE, DF lần lượt vuông góc với AB, AC tại E và F.

Do đó, $\widehat{DFC\text{}}=\widehat{DFA}=\widehat{DEA}=\widehat{DEB}=90°$.

Xét tứ giác AEDF có: $\widehat{DFA}=\widehat{DEA}=\widehat{FAE}=90°$.

Nên tứ giác AEDF là hình chữ nhật.

Do đó, $\widehat{FDE}=90°$.

Mà $\widehat{CDF}+\widehat{FDE}+\widehat{EDB}=180°$. Suy ra $\widehat{CDF}+\widehat{EDB}=90°$.

Xét tam giác BDE và tam giác DCF có:

$\widehat{DEB}=\widehat{DFC}=90°$

$\widehat{B}=\widehat{FDC}$$\left(=90°-\widehat{EDB}\right)$

Do đó, ∆BDE ᔕ ∆DCF (g.g).

b) Tam giác ABC có: DE // AC (cùng vuông góc với AB).

Nên ∆BDE ᔕ ∆BCA.

Do đó, $\frac{ED}{AC}=\frac{EB}{AB}=\frac{BD}{BC}$.

Suy ra $\frac{DE}{4}=\frac{EB}{3}=\frac{2}{5}$.

Do đó, DE = $\frac{8}{5}$cm, EB = $\frac{6}{5}$cm.

Suy ra AE = AB – EB = 3 – $\frac{6}{5}$$\frac{9}{5}$ cm.

Áp dụng định lí Pythagore vào tam giác AED vuông tại E có:

AD² = AE² + ED² = ${\left(\frac{9}{5}\right)}^2+{\left(\frac{8}{5}\right)}^2=\frac{29}{5}$.

Suy ra $AD=\sqrt{\frac{29}{5}}$ cm.

Bài tập 14 trang 83 SBT Toán lớp 8 Tập 2: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 10 cm, cạnh bên SD = 15 cm. Gọi O là giao điểm của AC và BD, M và N lần lượt là trung điểm của AB và CD.

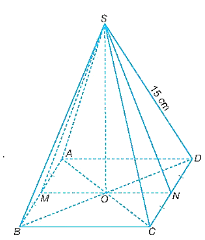
a) Chứng minh SO ⊥ MN. Từ đó tính độ dài đường cao SO của hình chóp.

b) Tính thể tích của hình chóp.

c) Tính diện tích toàn phần của hình chóp.

Lời giải:

a) Vì các mặt bên của hình chóp tứ giác đều là các tam giác cân bằng nhau nên các đường trung tuyến tương ứng của chúng bằng nhau, tức là SM = SN.

Do đó, tam giác SMN là tam giác cân tại S và O là trung điểm của MN nên SO ⊥ MN.

(Vì M và N lần lượt là trung điểm của AB và CD trong hình vuông ABCD với O là giao điểm của hai đường chéo nên ta chứng minh được O là trung điểm của MN).

Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore ta có:

AC² = AB² + BC² = 10² + 10² = 200 nên AC = $10\sqrt{2}$ cm.

Do đó, BD = AC = $10\sqrt{2}$ cm, suy ra DO = $\frac{1}{2}$BD = $5\sqrt{2}$ cm.

Xét tam giác SOD vuông tại O, áp dụng định lý Pythagore ta có:

DO² + SO² = SD²

Suy ra SO² = SD² – DO² = 15² – ${\left(5\sqrt{2}\right)}^2$ = 175.

Nên SO = $\sqrt{175}=5\sqrt{7}$ cm.

b) Thể tích của hình chóp tứ giác đều S.ABCD là:

$V_{S.ABCD}=\frac{1}{3}\cdot SO\cdot S_{ABCD}=\frac{1}{3}\cdot 5\sqrt{7}\cdot {10}^2=\frac{500\sqrt{7}}{3}$ (cm³).

c) Ta có SM là trung tuyến trong tam giác cân SAB nên SM đồng thời là đường cao.

Do đó, SM là một trung đoạn của hình chóp tứ giác đều.

Ta có SA = SD = 15 cm, AM = $\frac{1}{2}$AB = 5 cm.

Xét tam giác SMA vuông tại M, áp dụng định lý Pythagore ta có:

SM² + AM² = SA²

Do đó, SM² = SA² – AM² = 15² – 5² = 200 nên SM = $10\sqrt{2}$ cm.

Nửa chu vi đáy ABCD là: p = 10 . 4 : 2 = 20 cm.

Diện tích xung quanh của hình chóp là:

$S_{xq}=SM\cdot p=10\sqrt{2}\cdot 20=200\sqrt{2}$ (cm²).

Diện tích đáy ABCD là: S_ABCD = 10² = 100 (cm²).

Diện tích toàn phần của hình chóp S.ABCD là:

$S_{tp}=S_{xq}+S_{ABCD}=200\sqrt{2}+100=100\left(2\sqrt{2}+1\right)$ (cm²).

Thống kê - sắc xuất

Bài tập 15 trang 83 SBT Toán lớp 8 Tập 2: Khảo sát trên 1 200 người trẻ tuổi ở Việt Nam với câu hỏi “Bạn sử dụng nguồn thông tin nào cho các vấn đề hiện tại?” với các lựa chọn Mạng xã hội, Internet, Ti vi, Bạn bè, Báo chí, Gia đình, Đài phát thanh, Giáo viên, Thành viên cộng đồng cho kết quả như sau:

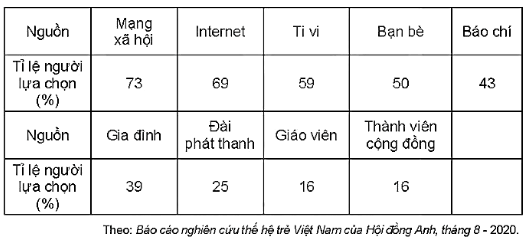
a) Dữ liệu nhóm khảo sát thu được từ câu hỏi trên thuộc loại nào?

b) Lựa chọn và vẽ biểu đồ biểu diễn dữ liệu trong bảng thống kê trên.

c) Tính tổng số lượng lựa chọn T cho các loại nguồn thông tin.

Giải thích tại sao T > 1 200

Lời giải:

a) Dữ liệu khảo sát thu được từ câu hỏi trên thuộc loại dữ liệu không là số, không thể sắp thứ tự.

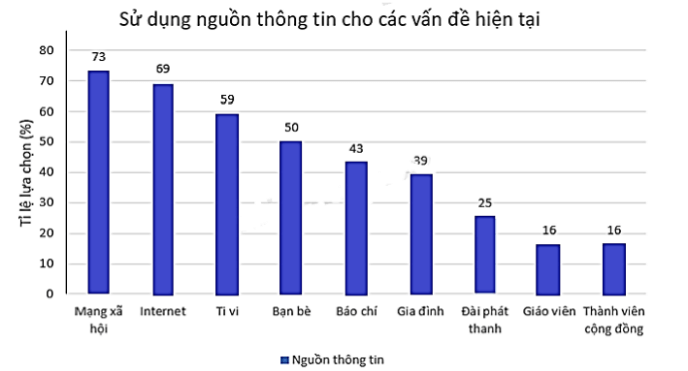
b) Ta dùng biểu đồ cột để biểu diễn dữ liệu trong bảng thống kê trên như sau:

c) Số người tham gia lựa chọn qua Mạng xã hội là: 1 200 ∙ 73% = 876 (người).

Số người tham gia lựa chọn qua Internet là: 1 200 ∙ 69% = 828 (người).

Số người tham gia lựa chọn qua Tivi là: 1 200 ∙ 59% = 708 (người).

Số người tham gia lựa chọn qua Bạn bè là: 1 200 ∙ 50% = 600 (người).

Số người tham gia lựa chọn qua Báo chí là: 1 200 ∙ 43% = 516 (người).

Số người tham gia lựa chọn qua Gia đình là: 1 200 ∙ 39% = 468 (người).

Số người tham gia lựa chọn qua Đài phát thanh là: 1 200 ∙ 25% = 300 (người).

Số người tham gia lựa chọn qua Giáo viên là: 1 200 ∙ 16% = 192 (người).

Số người tham gia lựa chọn qua Thành viên cộng đồng là: 1 200 ∙ 16% = 192 (người).

Tổng số lựa chọn là:

T = 876 + 828 + 708 + 600 + 516 + 468 + 300 + 192 + 192 = 4 680.

Do đó, T > 1 200. Điều này xảy ra bởi vì một người có thể có nhiều lựa chọn.

Bài tập 16 trang 83 SBT Toán lớp 8 Tập 2: Một túi đựng 24 viên vi giống hệt nhau chỉ khác màu, với 9 viên bi màu đỏ, 6 viên bi màu xanh, 4 viên bi màu vàng và 5 viên bi màu đen. Bạn Mai rút ngẫu nhiên một viên bi từ túi.

a) Có bao nhiêu kết quả có thể?

b) Chứng tỏ rằng các kết quả có thể không đồng khả năng. Tính xác suất để xảy ra mỗi kết quả có thể đó.

c) Tính xác suất để rút được viên bi màu đỏ hoặc màu vàng.

d) Tính xác suất để rút được viên bi không có màu đen.

Lời giải:

a) Có 24 viên bi giống hệt nhau chỉ khác màu với bốn màu là: màu đỏ, màu xanh, màu vàng, màu đen. Do đó, có bốn kết quả có thể là: Rút được viên bi màu đỏ; Rút được viên bi màu xanh; Rút được viên bi màu vàng; Rút được viên bi màu đen.

b) Vì số lượng viên bi mỗi màu khác nhau nên các kết quả có thể không đồng khả năng.

Gọi A là biến cố “Rút được viên bi màu đỏ”. Do bạn Mai rút ngẫu nhiên 1 viên bi từ trong túi có 24 viên bi nên có 24 kết quả đồng khả năng.

Vì có 9 viên bi màu đỏ nên số kết quả thuận lợi của A là 9. Xác suất của biến cố A là: $P\left(A\right)=\frac{9}{24}=\frac{3}{8}$.

Gọi B là biến cố: “Rút được viên bi màu xanh”. Vì có 6 viên bi màu xanh nên số kết quả thuận lợi của B là 6. Xác suất của biến cố B là: $P\left(B\right)=\frac{6}{24}=\frac{1}{4}$.

Gọi C là biến cố: “Rút được viên bi màu vàng”. Vì có 4 viên bi màu vàng nên số kết quả thuận lợi của C là 4. Xác suất của biến cố C là: $P\left(C\right)=\frac{4}{24}=\frac{1}{6}$.

Gọi D là biến cố: “Rút được viên bi màu đen”. Vì có 5 viên bi màu đen nên số kết quả thuận lợi của D là 5. Xác suất của biến cố D là: $P\left(D\right)=\frac{5}{24}$.

c) Gọi E là biến cố: “Rút được viên bi màu đỏ hoặc màu vàng”. Vì có 9 viên bi màu đỏ và 4 viên bi vàng nên số kết quả thuận lợi của E là: 9 + 4 = 13.

Xác suất của biến cố E là: $P\left(E\right)=\frac{13}{24}$.

d) Gọi F là biến cố: “Rút được viên bi không có màu đen”. Vì có 9 viên bi màu đỏ, 4 viên bi vàng, 6 viên bi màu xanh nên số kết quả thuận lợi của F là: 9 + 4 + 6 = 19. (Hoặc sử dụng do có 5 viên bi màu đen nên số viên bi không có màu đen là 24 – 5 = 19).

Xác suất của biến cố F là: $P\left(F\right)=\frac{19}{24}$.