Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC

Bài tập 12 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có đường cao AH. Lấy các điểm E, F lần lượt trên AB, AC sao cho HE, HF lần lượt vuông góc với AB, AC. Lấy điểm D trên EF sao cho AD vuông góc với EF. Đường thẳng AD cắt BC tại M. Chứng minh rằng:

a) AE . AB = AF . AC.

b) ∆ADE ᔕ ∆AHC và ∆ANF ᔕ ∆AMB.

Trả lời

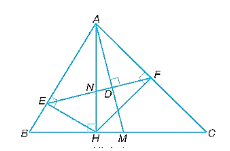
a) Vì AH là đường cao của tam giác ABC nên$\widehat{AHB}=\widehat{AHC}=90°$.

Vì HE, HF vuông góc với AB, AC nên ta có:

$\widehat{HEB}=\widehat{HEA}=\widehat{HFA}=\widehat{HFC}=90°$.

Tam giác HEA và tam giác BHA có:

$\widehat{HEA}=\widehat{AHB}=90°$

$\widehat{BAH}$chung

Do đó, ∆HEA ᔕ ∆BHA (g.g).

Suy ra $\frac{AE}{AH}=\frac{AH}{AB}$ nên AE . AB = AH² (1).

Tam giác HFA và tam giác CHA có:

$\widehat{HFA}=\widehat{AHC}=90°$

$\widehat{CAH}$ chung

Do đó, ∆HFA ᔕ ∆CHA (g.g).

Suy ra $\frac{AF}{AH}=\frac{AH}{AC}$nên AF . AC = AH² (2).

Từ (1) và (2) suy ra AE . AB = AF . AC.

b) Vì AE . AB = AF . AC nên$\frac{AE}{AC}=\frac{AF}{AB}$.

Tam giác AEF và tam giác ACB có:

$\frac{AE}{AC}=\frac{AF}{AB}$

$\widehat{BAC}$ chung

Do đó, ∆AEF ᔕ ∆ACB (c.g.c).

Suy ra $\widehat{AEF}=\widehat{C}$.

Tam giác AED và tam giác ACH có:

$\widehat{ADE}=\widehat{AHC}=90°$

$\widehat{AEF}=\widehat{C}$ (cmt)

Do đó, ∆ADE ᔕ ∆AHC (g.g).

Suy ra $\widehat{EAD}=\widehat{CAH}$.

Do đó, $\widehat{NAF}=\widehat{CAH}=\widehat{EAD}=\widehat{MAB}$.

Hai tam giác ANF và AMB có:

$\widehat{NAF}=\widehat{MAB}$  (chứng minh trên)

$\widehat{AFN}=\widehat{AFE}=\widehat{ABC}=\widehat{ABM}$ (do ∆AEF ᔕ ∆ACB)

Do đó ∆ANF ᔕ ∆AMB (g.g).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: