Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho MB/MA = 1/3, N là điểm trên cạnh BC sao cho NB/NC = 1/3

Bài tập 11 trang 82 SBT Toán lớp 8 Tập 2: Cho tam giác ABC. Giả sử M là điểm trên cạnh AB sao cho $\frac{MB}{MA}=\frac{1}{3}$, N là điểm trên cạnh BC sao cho $\frac{NB}{NC}=\frac{1}{3}$.

a) Chứng minh MN // AC và MN = $\frac{1}{4}$AC.

b) Gọi K là giao điểm của AN và CM. Chứng minh $\frac{KN}{KA}=\frac{KM}{KC}=\frac{1}{4}$.

c) Nếu thay điều kiện $\frac{MB}{MA}=\frac{1}{3}$ và $\frac{NB}{NC}=\frac{1}{3}$bằng điều kiện CM là phân giác của góc C, AN là phân giác của góc A thì tam giác ABC phải thỏa mãn điều kiện gì để MN // AC?

Trả lời

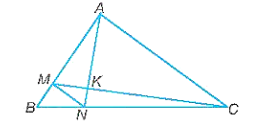
a) Xét tam giác ABC có:

$\frac{MB}{MA}=\frac{NB}{NC}\left(=\frac{1}{3}\right)$

Nên MN // AC (định lí Thalès đảo).

Vì $\frac{MB}{MA}=\frac{1}{3}$ nên MA = 3MB.

Tam giác ABC có MN // AC nên $\frac{MN}{AC}=\frac{BM}{AB}=\frac{BM}{BM+MA}=\frac{BM}{4BM}=\frac{1}{4}$.

Suy ra MN = $\frac{1}{4}$AC.

b) Tam giác MNK có MN // AC nên $\frac{KN}{KA}=\frac{KM}{KC}=\frac{MN}{AC}=\frac{1}{4}$.

c) Nếu MN // AC thì $\frac{MB}{MA}=\frac{NB}{NC}$ (định lí Thalès) (1).

Vì CM là tia phân giác của góc BCA trong tam giác ABC nên $\frac{MB}{MA}=\frac{BC}{AC}$ (2).

Vì AN là tia phân giác của góc BAC trong tam giác ABC nên $\frac{NB}{NC}=\frac{AB}{AC}$ (3).

Từ (1), (2), (3) suy ra $\frac{AB}{AC}=\frac{BC}{AC}$ nên AB = BC.

Do đó, tam giác ABC cân tại B.

Ngược lại, nếu tam giác ABC cân tại B, CM là phân giác của góc C, AN là phân giác góc A thì dễ thấy MN // AC.

Vậy để MN // AC thì điều kiện là tam giác ABC cân tại B.

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: