Cho hình thang cân ABCD có AB // CD, AB < CD, hai đường chéo AC và BD cắt nhau tại P, hai cạnh bên AD và BC kéo dài cắt nhau tại Q

Bài 12 trang 92 SBT Toán 8 Tập 1: Cho hình thang cân $ABCD$ có $AB//CD,AB<CD$, hai đường chéo $AC$ và $BD$ cắt nhau tại $P$, hai cạnh bên $AD$ và $BC$ kéo dài cắt nhau tại $Q$. Chứng minh $PQ$ là đường trung trực của hai đáy hình thang cân $ABCD$.

Trả lời

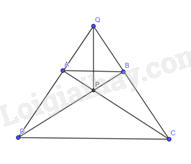
$\mathrm{\Delta }ACD=\mathrm{\Delta }BDC$ (c.g.c). Suy ra $\widehat{PCD}=\widehat{PDC}$

Do đó, tam giác $PCD$ cân tại $P$. Suy ra $PC=PD$

Mà $AC=BD$, suy ra $PA=PB$

Do $AB//CD$ nên $\widehat{QAB}=\widehat{ADC};\widehat{QBA}=\widehat{BCD}$ (các cặp góc đồng vị)

Mặt khác, $\widehat{ADC}=\widehat{BCD}$ nên $\widehat{QAB}=\widehat{QBA}$

Do đó, tam giác $QAB$ cân tại $Q$. Suy ra $QA=QB$

Mà $AD=BC$, suy ra $QD=QC$

Ta có: $PA=PB,PC=PD$ và $QA=QB,QC=QD$ nên $PQ$ là đường trung trực của cả hai đoạn thẳng $AB$ và $CD$.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi