Cho tứ giác ABCD có góc C = góc D và AD = BC. Chứng minh tứ giác ABCD là hình thang cân
Bài 11 trang 92 SBT Toán 8 Tập 1: Cho tứ giác ABCD có ˆC=ˆD và AD=BC. Chứng minh tứ giác ABCD là hình thang cân.
Bài 11 trang 92 SBT Toán 8 Tập 1: Cho tứ giác ABCD có ˆC=ˆD và AD=BC. Chứng minh tứ giác ABCD là hình thang cân.
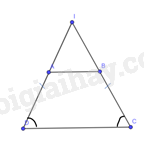
Gọi I là giao điểm của AD và BC
Do ˆC=ˆD nên tam giác ICD cân tại I. Suy ra ID=IC
Mà AD=BC, suy ra IA=IB. Do đó, tam giác IAB cân tại I.
Vì hai tam giác IAB và ICD đều cân tại I nên
^IAB=ˆD (cùng bằng 180∘−ˆI2)
Mà ^IAB và ˆD nằm ở vị trí đồng vị, suy ra AB//CD
Tứ giác ABCD có AB//CD và ˆC=ˆD nên ABCD là hình thang cân.
Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác: