Giải SBT Toán 7 (Cánh diều) Bài 4: Phép nhân đa thức một biến

Giải Sách bài tập Toán lớp 7 Bài 4: Phép nhân đa thức một biến

Bài 31 trang 49 SBT Toán 7 Tập 1: 

Tính:

a) $\frac{1}{4}x.\left(\frac{1}{2}{x}^2\right).\left(-\frac{4}{5}{x}^3\right)$;

b) 0,5x^{m + 1} . 0,8x ^{m – 1} (m ∈ ℕ, m ≥ 1);

c) $\left(x^2-3x+\frac{1}{4}\right)\left(-3x^3\right)$;

d) (x – 2)(x² + x – 1) – x(x² – 1).

Lời giải

a) $\frac{1}{4}x.\left(\frac{1}{2}{x}^2\right).\left(-\frac{4}{5}{x}^3\right)$

$=\frac{1}{4}.\frac{1}{2}.\left(-\frac{4}{5}\right)$. x . x² . x³ 

= $-\frac{1}{10}$x⁶.

b) 0,5x^{m + 1} . 0,8x ^{m – 1} 

= 0,5 . 0, 8 . x^{m + 1} . x ^{m – 1} 

= 0,4x^{m + 1 + m – 1} 

= 0,4x^2m.

c) $\left(x^2-3x+\frac{1}{4}\right)\left(-3x^3\right)$ 

= x² . (–3x³) – 3x . (–3x³) + $\frac{1}{4}$ . (–3x³)

= –3x⁵ + 9x⁴ – $\frac{3}{4}$x³.

d) (x – 2)(x² + x – 1) – x(x² – 1)

= x(x² + x – 1) – 2(x² + x – 1) – x . x² ‒ x . (‒1)

= x . x² + x . x ‒ x . 1 – 2 . x² – 2 . x – 2 . (‒1) – x³ + x

= x³ + x² – x – 2x² – 2x + 2 – x³ + x

= (x³ – x³) + (x² – 2x²) + (‒ x – 2x + x) + 2

= ‒ x² – 2x + 2.

Bài 32 trang 49 SBT Toán 7 Tập 1: 

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) (x + 0,5)(x² + 2x – 0,5) = x³ + 2,5x² – 0,5x – 0,25.

b) (x + 0,5)(x – 0,5) = x² – 0,25.  

c) $\frac{1}{2}{x}^3\left(2x-1\right)\left(\frac{1}{4}x+1\right)=\frac{1}{5}{x}^5-\frac{7}{4}{x}^4-\frac{1}{2}{x}^3.$ 

Lời giải

a) (x + 0,5)(x² + 2x – 0,5)

= x . (x² + 2x – 0,5) + 0,5 . (x² + 2x – 0,5)

= x . x² + x . 2x – x . 0,5 + 0,5 . x² + 0,5 . 2x – 0,5 . 0,5

= x³ + 2x² – 0,5x + 0,5x² + x – 0,25

= x³ + (2x² + 0,5x²) + (– 0,5x + x) + 0,25

= x³ + 2,5x² + 0,5x – 0,25.

Do đó phát biểu a) là sai.

b) (x + 0,5)(x – 0,5)

= x . (x – 0,5) + 0,5 . (x – 0,5)

= x . x – x . 0,5 + 0,5 . x – 0,5 . 0,5

= x² – 0,5x + 0,5x – 0,25

= x² – 0,25.  

Do đó phát biểu b) là đúng.

c) $\frac{1}{2}{x}^3\left(2x-1\right)\left(\frac{1}{4}x+1\right)$

$=\left(\frac{1}{2}{x}^3.2x-\frac{1}{2}{x}^3.1\right)\left(\frac{1}{4}x+1\right)$

$=\left(x^4-\frac{1}{2}{x}^3\right)\left(\frac{1}{4}x+1\right)$

$=x^4.\left(\frac{1}{4}x+1\right)-\frac{1}{2}{x}^3.\left(\frac{1}{4}x+1\right)$

$=x^4.\frac{1}{4}x+x^4.1-\frac{1}{2}{x}^3.\frac{1}{4}x-\frac{1}{2}{x}^3.1$

$=\frac{1}{4}{x}^5+x^4-\frac{1}{8}{x}^4-\frac{1}{2}{x}^3$

$=\frac{1}{4}{x}^5+\left(x^4-\frac{1}{8}{x}^4\right)-\frac{1}{2}{x}^3$

$=\frac{1}{4}{x}^5+\frac{7}{8}{x}^4-\frac{1}{2}{x}^3.$

Do đó phát biểu c) là sai.

Bài 33 trang 49, 50 SBT Toán 7 Tập 1: 

Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào biến:

a) x(2x + 1) – x²(x + 2) + (x³ – x + 3);

b) $\mathrm{0,2}\left(5x-3\right)-\frac{1}{2}\left(\frac{2}{3}x+6\right)+\frac{2}{3}\left(3-x\right);$ 

c) (2x – 9)(2x + 9) – 4x²;

d) (x² + 3x + 9)(x – 3) – (x³ + 23).

Lời giải

a) x(2x + 1) – x²(x + 2) + (x³ – x + 3)

= x . 2x + x . 1 – x² . x – x² . 2 + x³ – x + 3

= 2x² + x – x³ – 2x² + x³ – x + 3

= (– x³ + x³) + (2x² – 2x²) + (x – x) + 3

= 3.

Giá trị biểu thức là hằng số (bằng 3) nên không phụ thuộc vào biến.

b) $\mathrm{0,2}\left(5x-3\right)-\frac{1}{2}\left(\frac{2}{3}x+6\right)+\frac{2}{3}\left(3-x\right)$ 

= 0,2 . 5x – 0,2 . 3 –  $\frac{1}{2}.\frac{2}{3}$x – $\frac{1}{2}$ . 6 + $\frac{2}{3}$ . 3 –  $\frac{2}{3}$ . x

= x – 0,6 – $\frac{1}{3}$x – 3 + 2 – $\frac{2}{3}$x

$=\left(x-\frac{1}{3}x-\frac{2}{3}x\right)$ + (– 0,6 – 3 + 2)

= –1,6.

Giá trị biểu thức là hằng số (bằng –1,6) nên không phụ thuộc vào biến.

c) (2x – 9)(2x + 9) – 4x²

= 2x . (2x + 9) – 9 . (2x + 9) – 4x²

= 2x . 2x + 2x . 9 – 9 . 2x – 9 . 9 – 4x²

= 4x² + 18x – 18x – 81 – 4x²

= (4x² – 4x²) + (18x – 18x) – 81

= – 81.

Giá trị biểu thức là hằng số (bằng –81) nên không phụ thuộc vào biến.

d) (x² + 3x + 9)(x – 3) – (x³ + 23).

= x² . (x – 3) + 3x . (x – 3) + 9 . (x – 3) – x³ – 23

= x² . x – x² . 3 + 3x . x – 3x . 3 + 9 . x – 9 . 3 – x³ – 23

= x³ – 3x² + 3x² – 9x + 9x – 27 – x³ – 23

= (x³ – x³) + (– 3x² + 3x²) + (– 9x + 9x) + (– 27 – 23)

= – 50.

Giá trị biểu thức là hằng số (bằng –50) nên không phụ thuộc vào biến.

Bài 34 trang 50 SBT Toán 7 Tập 1: 

Chứng minh:

a) (x + 1)(x² – x + 1) = x³ – 1.

b) (x³ + x² + x  + 1)(x – 1) = x⁴ – 1.

c) (x + a)(x + b) = x² + (a + b)x + ab (với a, b là số thực).

Lời giải

a) (x + 1)(x² – x + 1)

= x . (x² – x + 1) + 1 . (x² – x + 1)

= x . x² – x . x + x . 1 + x² –  x + 1

= x³ – x² + x + x² –  x + 1

= x³ + (– x² + x²) + (x – x) + 1

= x³ – 1.

Vậy (x + 1)(x² – x + 1) = x³ – 1.

b) (x³ + x² + x  + 1)(x – 1)

= x³ . (x – 1) + x² . (x – 1) + x . (x – 1) + 1. (x – 1)

= x³ . x – x³ . 1 + x² . x – x² . 1 + x . x – x . 1 + x – 1

= x⁴ – x³ + x³ – x² + x² – x + x – 1

= x⁴ + (– x³ + x³) + (– x² + x²) + (– x + x) – 1

= x⁴ – 1.

Vậy (x³ + x² + x  + 1)(x – 1) = x⁴ – 1.

c) (x + a)(x + b)

= x . (x + b) + a . (x + b)

= x . x + x . b + a . x + ab

= x² + (bx + ax) + ab

= x² + (a + b)x + ab.

Vậy (x + a)(x + b) = x² + (a + b)x + ab (với a, b là số thực).

Bài 35 trang 50 SBT Toán 7 Tập 1: 

Tính giá trị của mỗi biểu thức sau:

a) 3(2x – 1) + 5(3 – x) tại $x=-\frac{3}{2}$;

b) 2x(6x – 1) – 3x(4x – 1) tại x = – 2 022;

c) (x – 2)(x² + x + 1) – x(x² – 1) tại x = 0,25;

d) 2x² + 3(x – 1)(x + 1) tại $x=\frac{1}{3}$.

Lời giải

a) Ta có:

3(2x – 1) + 5(3 – x)

= 3 . 2x – 3 . 1 + 5 . 3 – 5 . x

= 6x – 3 + 15 – 5x

= x + 12

Thay x = $-\frac{3}{2}$ vào biểu thức x + 12 ta được:

$-\frac{3}{2}$ + 12 = $\frac{-3+24}{2}=\frac{21}{2}.$

Vậy với x = $-\frac{3}{2}$ thì giá trị của biểu thức đã cho là $\frac{21}{2}.$

b) Ta có:

2x(6x – 1) – 3x(4x – 1)

= 2x . 6x – 2x . 1 – 3x . 4x – 3x . (–1)

= 12x² – 2x – 12x² + 3x

= (12x² – 12x²) + (– 2x + 3x)

= x.

Thay x = – 2 022 vào biểu thức vừa thu gọn ta được – 2 022.

Vậy với x = – 2 022 thì giá trị biểu thức đã cho là – 2 022.

c) Ta có:

(x – 2)(x² + x + 1) – x(x² – 1)

= x . (x² + x + 1) – 2 . (x² + x + 1) – x . x² – x . (–1)

= x . x² + x . x + x . 1 – 2 . x² – 2 . x – 2 . 1 – x³ + x

= x³ + x² + x – 2x² – 2x – 2 – x³ + x

= (x³ – x³) + (x² – 2x²) + (x – 2x + x) – 2

= – x² – 2.

Thay x = 0,25 vào biểu thức vừa thu gọn ta được:

– 0,25² – 2 = –0,0625 – 2 = –2,0625.

Vậy với x = 0,25 thì giá trị biểu thức đã cho là –2,0625.

d) Ta có:

2x² + 3(x – 1)(x + 1)

= 2x² + (3 . x – 3 . 1)(x + 1)

= 2x² + (3x – 3)(x + 1)

= 2x² + 3x . (x + 1) – 3 . (x + 1)

= 2x² + 3x . x + 3x . 1 – 3 . x – 3 . 1

= 2x² + 3x² + 3x – 3x – 3

= (2x² + 3x²) + (3x – 3x) – 3

= 5x² – 3.

Thay x = $\frac{1}{3}$ vào biểu thức vừa thu gọn ta được:

$5.{\left(\frac{1}{3}\right)}^2-3=5.\frac{1}{9}-3=\frac{5}{9}-\frac{27}{9}=-\frac{22}{9}$

Vậy với x = $\frac{1}{3}$ thì giá trị biểu thức đã cho là $-\frac{22}{9}.$

Bài 36 trang 50 SBT Toán 7 Tập 1: 

Xét đa thức P(x) = (2x² + a)(2x³ – 3) – 5a(x + 3) + 1 (với a là một số).

a) Thu gọn và sắp xếp đa thức P(x) theo số mũ giảm dần của biến.

b) Tìm a sao cho tổng các hệ số của đa thức P(x) bằng – 37.

Lời giải

a) Ta có:

P(x) = (2x² + a)(2x³ – 3) – 5a(x + 3) + 1

        = 2x² . (2x³ – 3) + a . (2x³ – 3) – 5a . x – 5a . 3 + 1

        = 2x² . 2x³ – 2x² . 3 + a . 2x³ – a . 3 – 5ax – 15a + 1

        = 4x⁵ – 6x² + 2ax³ – 3a – 5ax – 15a + 1

        = 4x⁵ + 2ax³ – 6x² – 5ax + (–15a – 3a) + 1

        = 4x⁵ + 2ax³ – 6x² – 5ax – 18a + 1

Vậy P(x) = 4x⁵ + 2ax³ – 6x² – 5ax – 18a + 1.

b) Đa thức P(x) có các hệ số là 4; 2a; –6; –5a; –18a; 1.

Tổng các hệ số của đa thức P(x) là:

4 + 2a + (–6) + (–5a) + (–18a) + 1 = – 21a – 1.

Theo bài ta có tổng các hệ số của đa thức P(x) bằng – 37.

Nên – 21a – 1 = – 37.

Suy ra – 21a = – 36

Do đó a = $\frac{36}{21}=\frac{12}{7}.$

Vậy a = $\frac{12}{7}.$

Bài 37 trang 50 SBT Toán 7 Tập 1: 

Bể cá cảnh nhà bạn Khôi có dạng lập phương với độ dài cạnh x (dm). Ban đầu mực nước ở bể cao x – 1 (dm), bạn Khôi đặt một khối đá núi cảnh chìm vào nước trong bể thì mực nước ở bể cao thêm 0,5 dm.

a) Tính thể tích nước có ở bể lúc đầu theo x.

b) Tính thể tích khối đá mà bạn Khôi thả chìm vào nước trong bể theo x.

c) Tính thể tích nước và khối đá mà bạn Khôi thả chìm vào nước trong bể theo x.

Lời giải

a) Ban đầu mực nước ở bể cao x – 1 (dm) nên thể tích nước có ở bể lúc đầu chính là thể tích của hình hộp chữ nhật có đáy là hình vuông cạnh x (dm) và chiều cao là x – 1 (dm).

Do đó thể tích nước có ở bể lúc đầu là:

x . x . (x – 1) = x² . (x – 1) = x³ – x² (dm³).

Vậy thể tích nước có ở bể lúc đầu là x³ – x² (dm³).

b) Thể tích của khối đá chính là thể tích phần nước dâng lên, bằng với thể tích của hình hộp chữ nhật có đáy là hình vuông cạnh x (dm) và chiều cao là 0,5 dm.

Do đó thể tích khối đá mà bạn Khôi thả chìm vào nước trong bể là:

x . x . 0,5 = 0,5x² (dm³).

Vậy thể tích khối đá mà bạn Khôi thả chìm vào nước trong bể là: 0,5x² (dm³).

c) Thể tích nước và khối đá mà bạn Khôi thả chìm vào nước trong bể là:

x³ – x² + 0,5x² = x³ + (– x² + 0,5x²) = x³ – 0,5x² (dm³).

Vậy thể tích nước và khối đá mà bạn Khôi thả chìm vào nước trong bể là x³ – 0,5x² (dm³).

Bài 38 trang 50 SBT Toán 7 Tập 1: 

Bác Na có mảnh đất được mô tả như Hình 4.

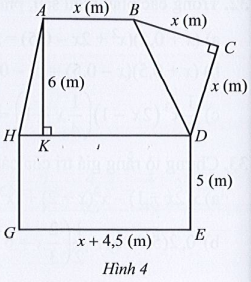
Bác chia mảnh đất đó thành các khu vực: khu trồng rau là hình thang ABDH (AB // DH, AK ⊥ HD), khu trồng cây ăn quả là tam giác BCD và khu chăn nuôi là hình chữ nhật HDEG. Tính diện tích của mảnh đất đó theo các kích thước AB = x (m), BC = x (m), CD = x (m), DE = 5 (m), EG = x + 4,5 (m), AK = 6 (m).

Lời giải

Diện tích khu trồng rau (diện tích hình thang ABDH) là:

$\frac{1}{2}$ . 6. [x + (x + 4,5)] = 3 . (2x + 4,5) = 6x + 13,5 (m²).

Diện tích khu trồng cây ăn quả (diện tích tam giác BCD) là:

$\frac{1}{2}$ . x . x = $\frac{1}{2}$x² (m²).

Diện tích khu chăn nuôi (diện tích hình chữ nhật HDEG) là:

5 . (x + 4,5) = 5x + 22,5 (m²).

Diện tích của mảnh đất đó là:

6x + 13,5 + $\frac{1}{2}$x² + 5x + 22,5

= $\frac{1}{2}$x² + (6x + 5x) + (13,5 + 22,5)

= $\frac{1}{2}$x² + 11x + 36 (m²).

Vậy diện tích của mảnh đất đó là $\frac{1}{2}$x² + 11x + 36 (m²).

Bài 39 trang 51 SBT Toán 7 Tập 1: 

Từ một tấm bìa có dạng hình chữ nhật với độ dài các cạnh là 37 cm và 27 cm, người ta cắt đi ở bốn góc của tấm bìa bốn hình vuông cạnh là x cm và xếp phần còn lại thành một hình hộp chữ nhật không nắp.

a) Tính diện tích xung quanh S(x) của hình hộp chữ nhật trên theo x.

b) Tính giá trị của S(x) tại x = 2.

Lời giải

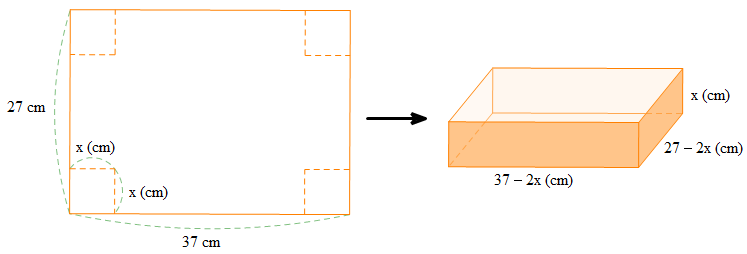
a) Chiều dài của hình hộp chữ nhật là: 37 – x – x = 37 – 2x (cm).

Chiều rộng của hình hộp chữ nhật là: 27 – x – x = 27 – 2x (cm).

Chiều cao của hình hộp chữ nhật chính là độ dài cạnh hình vuông bị cắt đi và bằng x (cm).

Khi đó diện tích xung quanh của hình hộp chữ nhật đó là:

S(x) = 2. [(37 – 2x) + (27 – 2x)] . x

= 2x . (64 – 4x) = 128x – 8x² (cm²).

Vậy diện tích xung quanh của hình hộp chữ nhật đó là S(x) = 128x – 8x² (cm²).

b) Thay x = 2 vào S(x) = 128x – 8x² ta được:

S(2) = 128 . 2 – 8 . 2² = 256 – 32 = 224 (cm²).

Vậy tại x = 2 thì S(x) có giá trị là 224 (cm²).

Bài 40 trang 51 SBT Toán 7 Tập 1: 

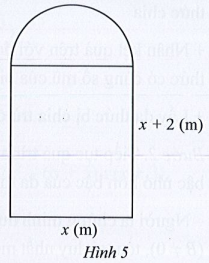
Một ngôi nhà có 4 ô cửa sổ, mỗi ô cửa sổ được mô tả như Hình 5 gồm một hình chữ nhật có độ dài các cạnh là x (m), x + 2 (m) và một nửa hình tròn. Người ta muốn ốp kính cường lực cho các ô cửa sổ đó. Hỏi cần bao nhiêu mét vuông kính (lấy π = 3,14)? Biết diện tích của phần khung gỗ là 0,42 m².

Lời giải

Diện tích của phần cửa có dạng hình chữ nhật là: x(x + 2) = x² + 2x (m²).

Cửa có dạng hình tròn có đường kính là x (m) nên có bán kính bằng $\frac{x}{2}$ (m).

Khi đó diện tích của phần cửa có dạng nửa hình tròn là:

$\frac{1}{2}\mathrm{.3,14.}{\left(\frac{x}{2}\right)}^2=\frac{1}{2}\mathrm{.3,14.}\frac{x^2}{4}$ = 0,3925x² (m²).

Số mét vuông kính cần sử dụng để ốp cho 1 ô cửa sổ là:

(x² + 2x) + 0,3925x² – 0,42 = 1,3925x² + 2x – 0,42 (m²).

Số mét vuông kính cần sử dụng để ốp cho 4 ô cửa sổ là:

4 . (1,3925x² + 2x – 0,42) = 5,57x² + 8x – 1,68 (m²).

Vậy cần sử dụng 5,57x² + 8x – 1,68 mét vuông kính để ốp cho 4 ô cửa sổ của ngôi nhà đó.

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

Bài 2. Đa thức một biến. Nghiệm của đa thức một biến

Bài 3. Phép cộng, phép trừ đa thức một biến

Bài 5. Phép chia đa thức một biến

Bài tập cuối chương 6

Bài 1. Tổng các góc của một tam giác