Giải SBT Toán 11 Bài 1: Đường thẳng và mặt phằng trong không gian
A. (ABCD)
B. (SAC)
C. (SAB)
D. (SAD)
Lời giải:
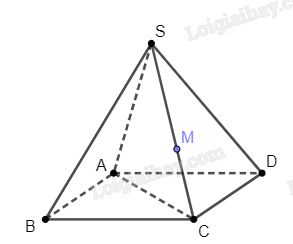
Theo hình vẽ, ta thấy SC nằm trong mặt (SAC).
Do M∈SC nên M nằm trên mặt phẳng (SAC).
Đáp án đúng là B.
A. AB
B. BD
C. CD
D. AC
Lời giải:
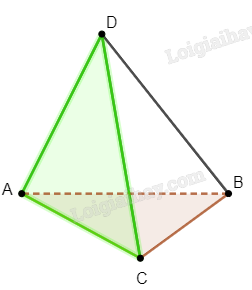
Xét hai mặt phẳng (ABC) và (CDA), ta nhận thấy hai mặt phẳng này có hai điểm chung là A và C, do đó giao tuyến của hai mặt phẳng này là AC.
Đáp án đúng là D.
Lời giải:
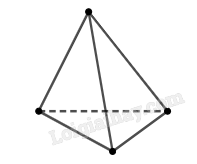
Do đồ vật trang trí có 4 mặt là các tam giác, nên nó có hình dạng một tứ diện.
Hình biểu diễn của nó như sau:
Lời giải:
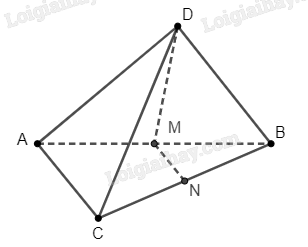
Do N là trung điểm của BC, nên 4 điểm B, N, C, D cùng nằm trong mặt phẳng.
Giả sử 4 điểm M, N, C, D cùng nằm trong một mặt phẳng.
Điều này có nghĩa là M∈(NCD).
Do bốn điểm B, N, C, D cùng nằm trong mặt phẳng, ta suy ra M∈(BCD).
Điểm M và điểm B cùng nằm trong mặt phẳng (BCD), nên BM⊂(BCD).
Mặt khác, do M là trung điểm của AB, nên A∈BM.
Suy ra A∈(BCD). Điều này là vô lí do ABCD là tứ diện nên bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng.
Lời giải:
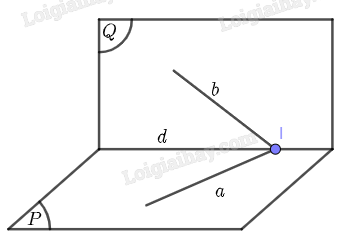
Gọi I là giao điểm của hai đường thẳng a và b. Suy ra {I∈aI∈b
Vì a⊂(P) và b⊂(Q), ta suy ra {I∈(P)I∈(Q), tức là I thuộc giao tuyến của hai mặt phẳng (P) và (Q). Mà (P)∩(Q)=d, suy ra I∈d.
Bài toán được chứng minh.
a) Xác định giao tuyến của mặt phẳng (BEF) với các mặt phẳng (ABC), (ACD), (BCD).
b) Xác định giao điểm K của đường thẳng AD với mặt phẳng (BEF).
c) Xác định giao tuyến của hai mặt phẳng (BEF) và (ABD).
Lời giải:
a)
Giao tuyến của (BEF) và (ABC):
Ta có B∈(BEF)∩(ABC).
Mặt khác, ta có {E∈(BEF)E∈AC⊂(ABC)⇒E∈(BEF)∩(ABC).
Như vậy giao tuyển của (BEF) và (ABC) là đường thẳng BE.
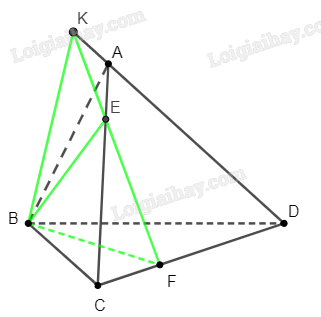
Giao tuyến của (BEF) và (ACD):
Ta có {F∈(BEF)F∈CD⊂(ACD)⇒F∈(BEF)∩(ACD).
Mặt khác, {E∈(BEF)E∈AC⊂(ACD)⇒E∈(BEF)∩(ACD).
Như vậy giao tuyển của (BEF) và (ACD) là đường thẳng EF.
Giao tuyến của (BEF) và (BCD):
Ta có B∈(BEF)∩(BCD)
Mặt khác, {F∈(BEF)F∈CD⊂(BCD)⇒F∈(BEF)∩(BCD)
Như vậy giao tuyển của (BEF) và (BCD) là đường thẳng BF.
b) Trên mặt phẳng (ACD), lấy K là giao điểm của AD và EF.
Ta có {K}=AD∩EF, mà EF⊂(BEF).
Suy ra {K}=AD∩(BEF), tức K là giao điểm của AD và (BEF).
c) Ta có B∈(BEF)∩(ABD).
Theo câu b, ta có K∈AD∩(BEF)⇒{K∈ADK∈(BEF)
Mà AD∈(ABD) nên ta suy ra {K∈(ABD)K∈(BEF)⇒K∈(ABD)∩(BEF).
Vậy giao tuyến của hai mặt phẳng (BEF) và (ABD) là đường thẳng BK.
a) Xác định giao điểm của đường thẳng NP với mặt phẳng (SAB).
b) Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SAB),(SAD),(SBC),(SCD).
Lời giải:
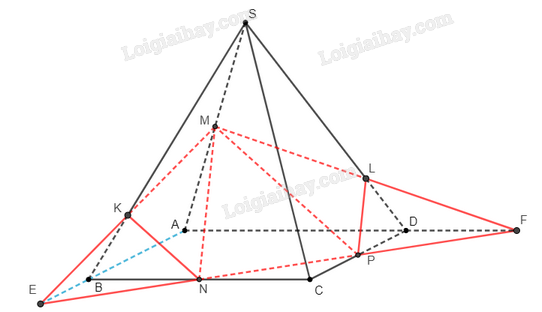
a) Xét mặt phẳng (ABCD), gọi E là giao điểm của AB và NP.
Ta có {E}=AB∩NP, mà NP⊂(MNP) nên {E}=(SAB)∩NP.
b)
Giao tuyến của (MNP) và (SAB):
Ta có {M∈SA⊂(SAB)M∈(MNP)⇒M∈(SAB)∩(MNP).
Mặt khác, theo câu a, ta có {E∈AB⊂(SAB)E∈NP⊂(MNP)⇒E∈(SAB)∩(MNP).
Từ đó, giao tuyến của hai mặt phẳng (SAB) và (MNP) là đường thẳng ME.
Giao tuyến của (MNP) và (SAD):
Trên mặt phẳng (ABCD), gọi F là giao điểm của AD và NP.
Vì F là giao điểm của AD và NP, ta suy ra {F∈ADF∈NP.
Do AD⊂(SAD), NP⊂(MNP) nên ta có {F∈(SAD)F∈(MNP)⇒F∈(SAD)∩(MNP).
Hơn nữa, ta cũng có {M∈SA⊂(SAD)M∈(MNP)⇒M∈(SAD)∩(MNP).
Vậy giao tuyến của hai mặt phẳng (SAD) và (MNP) là đường thẳng MF.
Giao tuyến của (MNP) và (SBC):
Ta có ME là giao tuyến của hai mặt phẳng (SAB) và (MNP)⇒ME⊂(SAB).
Trên mặt phẳng (SAB), gọi {K}=ME∩SB.
Suy ra {K∈ME⊂(MNP)K∈SB⊂(SBC)⇒K∈(MNP)∩(SBC).
Hơn nữa, ta có {N∈(MNP)N∈BC⊂(SBC)⇒N∈(MNP)∩(SBC).
Vậy giao tuyến của hai mặt phẳng (SBC) và (MNP) là đường thẳng NK.
Giao tuyến của (MNP) và (SCD):
Ta có MF là giao tuyến của hai mặt phẳng (SAD) và (MNP)⇒MF⊂(SAD).
Trên mặt phẳng (SAD), gọi {L}=MF∩SD.
Suy ra {L∈MF⊂(MNP)L∈SD⊂(SCD)⇒L∈(MNP)∩(SCD).
Hơn nữa, ta có {P∈(MNP)P∈CD⊂(SCD)⇒P∈(MNP)∩(SCD).
Vậy giao tuyến của hai mặt phẳng (SCD) và (MNP) là đường thẳng LP.
a) Xác định giao điểm I của đường thẳng MP với mặt phẳng (SBD).
b) Xác định giao điểm Q của đường thẳng SD với mặt phẳng (MNP).
Lời giải:
a) Trên mặt phẳng (ABCD), gọi {O}=AC∩BD.
Trên mặt phẳng (SAC), gọi {I}=MP∩SO.
Do SO⊂(SBD), ta suy ra {I}=MP∩(SBD).
Vậy I là giao điểm của MP và (SBD).
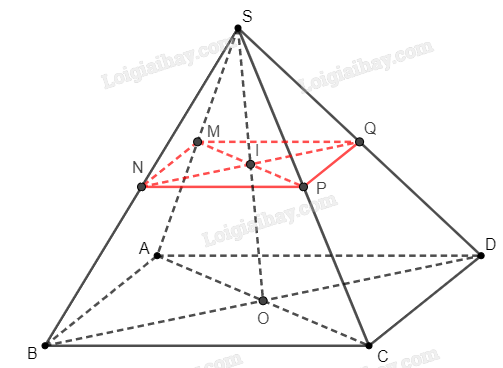
b) Trên mặt phẳng (SBD), gọi {Q}=NI∩SD.
Do NI⊂(MNP), ta suy ra {Q}=(MNP)∩SD.
Vậy Q là giao điểm của SD và (MNP).
a) Xác định các giao điểm M, N lần lượt của SA, SD với mặt phẳng (IBC).
b*) Chứng minh rằng các đường thẳng AD, BC và MN đồng quy.
Lời giải:
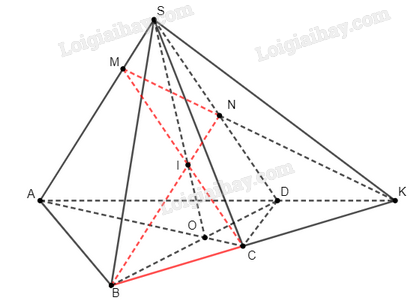
a)
Giao điểm M của SA và (IBC):
Ta nhận xét rằng I∈SO⊂(SAC)⇒CI⊂(SAC).
Trên mặt phẳng (SAC), gọi {M}=CI∩SA.
Do IC⊂(IBC), nên {M}=(IBC)∩SA.
Vậy M là giao điểm của (IBC) và SA.
Giao điểm N của SD và (IBC):
Ta nhận xét rằng I∈SO⊂(SBD)⇒BI⊂(SBD).
Trên mặt phẳng (SBD), gọi {N}=BI∩SD.
Do IB⊂(IBC), nên {N}=(IBC)∩SD.
Vậy N là giao điểm của (IBC) và SD.
b) Trên mặt phẳng (ABCD), gọi K là giao điểm của AD và BC.
Ta có {M∈SA⊂(SAD)M∈(IBC)⇒M∈(SAD)∩(IBC).
Mặt khác, {N∈SD⊂(SAD)N∈(IBC)⇒N∈(SAD)∩(IBC).
Vậy giao tuyến của (SAD) và (IBC) là đường thẳng MN.
Do AD∈(SAD), BC∈(IBC), {K}=AD∩BC, ta suy ra K nằm trên giao tuyến của (SAD) và (IBC), tức là K∈MN.
Vậy ba đường thẳng AD, BC, MN cắt nhau tại K.
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian




