Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD

Trả lời

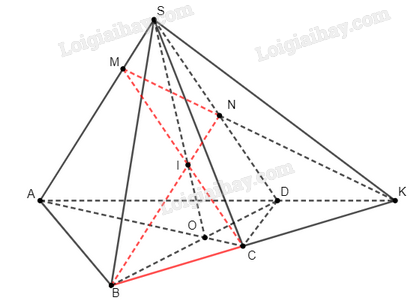
a)

Giao điểm $M$ của $SA$ và $\left(IBC\right)$:

Ta nhận xét rằng $I\in SO\subset \left(SAC\right)\Rightarrow CI\subset \left(SAC\right)$.

Trên mặt phẳng $\left(SAC\right)$, gọi $\left\{M\right\}=CI\cap SA$.

Do $IC\subset \left(IBC\right)$, nên $\left\{M\right\}=\left(IBC\right)\cap SA$.

Vậy $M$ là giao điểm của $\left(IBC\right)$ và $SA$.

Giao điểm $N$ của $SD$ và $\left(IBC\right)$:

Ta nhận xét rằng $I\in SO\subset \left(SBD\right)\Rightarrow BI\subset \left(SBD\right)$.

Trên mặt phẳng $\left(SBD\right)$, gọi $\left\{N\right\}=BI\cap SD$.

Do $IB\subset \left(IBC\right)$, nên $\left\{N\right\}=\left(IBC\right)\cap SD$.

Vậy $N$ là giao điểm của $\left(IBC\right)$ và $SD$.

b) Trên mặt phẳng $\left(ABCD\right)$, gọi $K$ là giao điểm của $AD$ và $BC$.

Ta có $\{\begin{array}{l}M\in SA\subset \left(SAD\right)\\ M\in \left(IBC\right)\end{array}\Rightarrow M\in \left(SAD\right)\cap \left(IBC\right)$.

Mặt khác, $\{\begin{array}{l}N\in SD\subset \left(SAD\right)\\ N\in \left(IBC\right)\end{array}\Rightarrow N\in \left(SAD\right)\cap \left(IBC\right)$.

Vậy giao tuyến của $\left(SAD\right)$ và $\left(IBC\right)$ là đường thẳng $MN$.

Do $AD\in \left(SAD\right)$, $BC\in \left(IBC\right)$, $\left\{K\right\}=AD\cap BC$, ta suy ra $K$ nằm trên giao tuyến của $\left(SAD\right)$ và $\left(IBC\right)$, tức là $K\in MN$.

Vậy ba đường thẳng $AD$, $BC$, $MN$ cắt nhau tại $K$.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song