Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, BC, CD

Bài 7 trang 95 SBT Toán 11: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N,P$ lần lượt là trung điểm của các cạnh $SA,BC,CD$.

a) Xác định giao điểm của đường thẳng $NP$ với mặt phẳng $\left(SAB\right)$.

b) Xác định giao tuyến của mặt phẳng $\left(MNP\right)$ với các mặt phẳng $\left(SAB\right),\left(SAD\right),\left(SBC\right),\left(SCD\right)$.

Trả lời

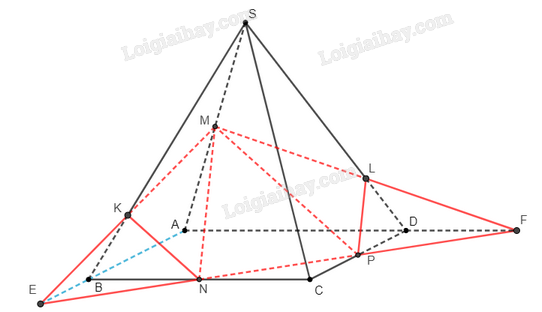
a) Xét mặt phẳng $\left(ABCD\right)$, gọi $E$ là giao điểm của $AB$ và $NP$.

Ta có $\left\{E\right\}=AB\cap NP$, mà $NP\subset \left(MNP\right)$ nên $\left\{E\right\}=\left(SAB\right)\cap NP$.

b)

Giao tuyến của $\left(MNP\right)$ và $\left(SAB\right)$:

Ta có $\{\begin{array}{l}M\in SA\subset \left(SAB\right)\\ M\in \left(MNP\right)\end{array}\Rightarrow M\in \left(SAB\right)\cap \left(MNP\right)$.

Mặt khác, theo câu a, ta có $\{\begin{array}{l}E\in AB\subset \left(SAB\right)\\ E\in NP\subset \left(MNP\right)\end{array}\Rightarrow E\in \left(SAB\right)\cap \left(MNP\right)$.

Từ đó, giao tuyến của hai mặt phẳng $\left(SAB\right)$ và $\left(MNP\right)$ là đường thẳng $ME$.

Giao tuyến của $\left(MNP\right)$ và $\left(SAD\right)$:

Trên mặt phẳng $\left(ABCD\right)$, gọi $F$ là giao điểm của $AD$ và $NP$.

Vì $F$ là giao điểm của $AD$ và $NP$, ta suy ra $\{\begin{array}{l}F\in AD\\ F\in NP\end{array}$.

Do $AD\subset \left(SAD\right)$, $NP\subset \left(MNP\right)$ nên ta có $\{\begin{array}{l}F\in \left(SAD\right)\\ F\in \left(MNP\right)\end{array}\Rightarrow F\in \left(SAD\right)\cap \left(MNP\right)$.

Hơn nữa, ta cũng có $\{\begin{array}{l}M\in SA\subset \left(SAD\right)\\ M\in \left(MNP\right)\end{array}\Rightarrow M\in \left(SAD\right)\cap \left(MNP\right)$.

Vậy giao tuyến của hai mặt phẳng $\left(SAD\right)$ và $\left(MNP\right)$ là đường thẳng $MF$.

Giao tuyến của $\left(MNP\right)$ và $\left(SBC\right)$:

Ta có $ME$ là giao tuyến của hai mặt phẳng $\left(SAB\right)$ và $\left(MNP\right)$$\Rightarrow ME\subset \left(SAB\right)$.

Trên mặt phẳng $\left(SAB\right)$, gọi $\left\{K\right\}=ME\cap SB$.

Suy ra $\{\begin{array}{l}K\in ME\subset \left(MNP\right)\\ K\in SB\subset \left(SBC\right)\end{array}\Rightarrow K\in \left(MNP\right)\cap \left(SBC\right)$.

Hơn nữa, ta có $\{\begin{array}{l}N\in \left(MNP\right)\\ N\in BC\subset \left(SBC\right)\end{array}\Rightarrow N\in \left(MNP\right)\cap \left(SBC\right)$.

Vậy giao tuyến của hai mặt phẳng $\left(SBC\right)$ và $\left(MNP\right)$ là đường thẳng $NK$.

Giao tuyến của $\left(MNP\right)$ và $\left(SCD\right)$:

Ta có $MF$ là giao tuyến của hai mặt phẳng $\left(SAD\right)$ và $\left(MNP\right)$$\Rightarrow MF\subset \left(SAD\right)$.

Trên mặt phẳng $\left(SAD\right)$, gọi $\left\{L\right\}=MF\cap SD$.

Suy ra $\{\begin{array}{l}L\in MF\subset \left(MNP\right)\\ L\in SD\subset \left(SCD\right)\end{array}\Rightarrow L\in \left(MNP\right)\cap \left(SCD\right)$.

Hơn nữa, ta có $\{\begin{array}{l}P\in \left(MNP\right)\\ P\in CD\subset \left(SCD\right)\end{array}\Rightarrow P\in \left(MNP\right)\cap \left(SCD\right)$.

Vậy giao tuyến của hai mặt phẳng $\left(SCD\right)$ và $\left(MNP\right)$ là đường thẳng $LP$.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song