Cho tứ diện ABCD. Trên các cạnh AC, CD lần lượt lấy các điểm E, F sao cho CE = 3EA, DF = 2FC

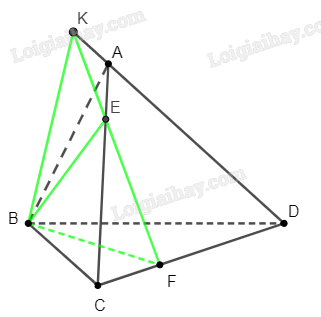
Bài 6 trang 95 SBT Toán 11: Cho tứ diện $ABCD$. Trên các cạnh $AC,CD$ lần lượt lấy các điểm $E,F$ sao cho $CE=3EA,DF=2FC$.

a)    Xác định giao tuyến của mặt phẳng $\left(BEF\right)$ với các mặt phẳng $\left(ABC\right)$, $\left(ACD\right)$, $\left(BCD\right)$.

b)    Xác định giao điểm $K$ của đường thẳng $AD$ với mặt phẳng $\left(BEF\right)$.

c)     Xác định giao tuyến của hai mặt phẳng $\left(BEF\right)$ và $\left(ABD\right)$.

Trả lời

a)

Giao tuyến của $\left(BEF\right)$ và $\left(ABC\right)$:

Ta có $B\in \left(BEF\right)\cap \left(ABC\right)$.

Mặt khác, ta có $\{\begin{array}{l}E\in \left(BEF\right)\\ E\in AC\subset \left(ABC\right)\end{array}\Rightarrow E\in \left(BEF\right)\cap \left(ABC\right)$.

Như vậy giao tuyển của $\left(BEF\right)$ và $\left(ABC\right)$ là đường thẳng $BE$.

Giao tuyến của $\left(BEF\right)$ và $\left(ACD\right)$:

Ta có $\{\begin{array}{l}F\in \left(BEF\right)\\ F\in CD\subset \left(ACD\right)\end{array}\Rightarrow F\in \left(BEF\right)\cap \left(ACD\right)$.

Mặt khác, $\{\begin{array}{l}E\in \left(BEF\right)\\ E\in AC\subset \left(ACD\right)\end{array}\Rightarrow E\in \left(BEF\right)\cap \left(ACD\right)$.

Như vậy giao tuyển của $\left(BEF\right)$ và $\left(ACD\right)$ là đường thẳng $EF$.

Giao tuyến của $\left(BEF\right)$ và $\left(BCD\right)$:

Ta có $B\in \left(BEF\right)\cap \left(BCD\right)$

Mặt khác, $\{\begin{array}{l}F\in \left(BEF\right)\\ F\in CD\subset \left(BCD\right)\end{array}\Rightarrow F\in \left(BEF\right)\cap \left(BCD\right)$

Như vậy giao tuyển của $\left(BEF\right)$ và $\left(BCD\right)$ là đường thẳng $BF$.

b) Trên mặt phẳng $\left(ACD\right)$, lấy $K$ là giao điểm của $AD$ và $EF$.

Ta có $\left\{K\right\}=AD\cap EF$,  mà $EF\subset \left(BEF\right)$.

Suy ra $\left\{K\right\}=AD\cap \left(BEF\right)$, tức $K$ là giao điểm của $AD$ và $\left(BEF\right)$.

c) Ta có $B\in \left(BEF\right)\cap \left(ABD\right)$.

Theo câu b, ta có $K\in AD\cap \left(BEF\right)\Rightarrow \{\begin{array}{l}K\in AD\\ K\in \left(BEF\right)\end{array}$

Mà $AD\in \left(ABD\right)$ nên ta suy ra $\{\begin{array}{l}K\in \left(ABD\right)\\ K\in \left(BEF\right)\end{array}\Rightarrow K\in \left(ABD\right)\cap \left(BEF\right)$.

Vậy giao tuyến của hai mặt phẳng $\left(BEF\right)$ và $\left(ABD\right)$ là đường thẳng $BK$.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 3: Đường thẳng và mặt phẳng song song

Bài 4: Hai mặt phẳng song song