Giải SBT Toán 11 Bài tập cuối chương 4 trang 117
A. Bốn điểm A, B, C, D đã cho đôi một khác nhau.
B. Không có ba điểm nào trong bốn điểm A, B, C, D là thẳng hàng.
C. Hai đường thẳng AC và BD song song với nhau.
D. Hai đường thẳng AC và BD không có điểm chung.
Lời giải:
Đáp án đúng là: C
Vì bốn điểm A, B, C, D không cùng thuộc một mặt phẳng nên hai đường thẳng AC và BD chéo nhau, do đó đáp án C sai.
A. 12.
B. 13.
C. 23.
D. 34.
Lời giải:
Đáp án đúng là: B
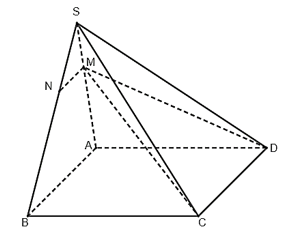
Vì ABCD là hình bình hành nên AB // CD.
Ta có M ∈ SA nên M ⊂ (SAB).
Hai mặt phẳng (SAB) và (MCD) có M là điểm chung và lần lượt chứa hai đường thẳng AB và CD song song với nhau nên giao tuyến của chúng là đường thẳng đi qua M và song song với AB.
Từ M, kẻ đường thẳng song song với AB, cắt SB tại N. Khi đó (SAB) ∩ (MCD) = MN.
Do vậy N là giao điểm của SB và mặt phẳng (MCD).
Ta có MA = 2MS ⇒SMSA=13.
Xét tam giác SAB có MN // AB, theo định lí Thalés ta có: SNSB=SMSA=13.
A. 12.
B. 1.
C. 2.
D. 3.
Lời giải:
Đáp án đúng là: C
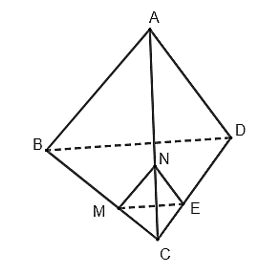
Trong mặt phẳng (BCD), từ M kẻ đường thẳng song song với BD cắt CD tại E.
Trong mặt phẳng (ABC), từ M kẻ đường thẳng song song với AB cắt AC tại N.
Từ đó suy ra (MNE) // (ABD) hay mặt phẳng (MNE) chính là mặt phẳng (P).
Ta có MB = 2MC ⇒BMMC=2.
Xét tam giác ABC có MN // AB, theo định lí Thalés ta có: ANNC=BMMC=2.
Lời giải:
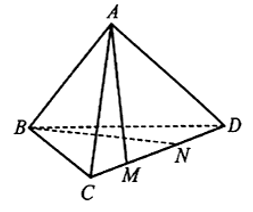
Giả sử hai đường thẳng AM và BN cắt nhau.
Khi đó, qua AM và BN có một mặt phẳng (P).
Do M, N thuộc (P) nên đường thẳng MN nằm trong (P) hay CD nằm trong (P).
Suy ra A, B, C, D cùng thuộc một mặt phẳng, mâu thuẫn với giả thiết.
Vậy AM và BN không cắt nhau.
Lời giải:

Do ba điểm A, B, C không thẳng hàng nên qua ba điểm A, B, C có một mặt phẳng, gọi là (ABC).
Vì M ∈ AB nên M ∈ (ABC).
Tương tự, ta có N và P đều thuộc (ABC).
Mà M, N, P đều thuộc mặt phẳng (P).
Suy ra M, N, P là ba điểm chung của hai mặt phẳng (ABC) và (P).
Do đó, M, N, P cùng thuộc giao tuyến của (ABC) và (P).
Vậy M, N, P thẳng hàng.
Bài 57 trang 118 SBT Toán 11: Cho hình chóp S.ABCD. Gọi M là trung điểm của cạnh SD.
a) Xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Xác định giao điểm của đường thẳng BM với mặt phẳng (SAC).
c) Xác định giao tuyến của mặt phẳng (MBC) với các mặt phẳng (SAB) và (SAD).
Lời giải:
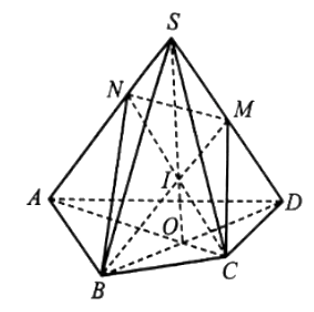
a) Hai mặt phẳng (SAC) và (SBD) có chung điểm S.
Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD. Khi đó, O là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD).
Vậy SO là giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Trong mặt phẳng (SBD), gọi I là giao điểm của BM và SO.
Vì I ∈ SO và SO ⊂ (SAC) nên I ∈ (SAC).
Vậy I là giao điểm của đường thẳng BM với mặt phẳng (SAC).
c) Trong mặt phẳng (SAC), gọi N là giao điểm của CI và SA.
Ta có N ∈ SA và SA ⊂ (SAB) nên N ∈ (SAB); N ∈ CI và CI ⊂ (MBC) nên N ∈ (MBC).
Do đó, N là một điểm chung của hai mặt phẳng (SAB) và (MBC).
Lại có hai mặt phẳng (SAB) và (MBC) có điểm chung B.
Do vậy, BN là giao tuyến của hai mặt phẳng (MBC) và (SAB).
Lại có N ∈ SA và SA ⊂ (SAD) nên N ∈ (SAD) nên N là điểm chung của hai mặt phẳng (MBC) và (SAD).
Vì M ∈ SD và SD ⊂ (SAD) nên M ∈ (SAD), mà M ∈ (MBC) nên M là một điểm chung của hai mặt phẳng (MBC) và (SAD).
Vậy giao tuyến của hai mặt phẳng (MBC) và (SAD) là đường thẳng MN.
Lời giải:
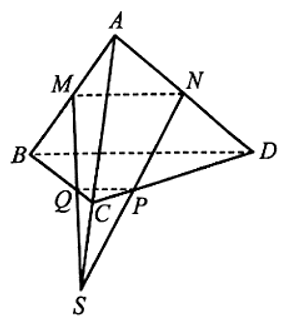
Giả sử M, N, P, Q cùng thuộc một mặt phẳng.
Xét tam giác ABC, do Q không là trung điểm của BC nên đường thẳng MQ cắt đường thẳng AC tại điểm S.
Khi đó, S ∈ (MNPQ) và S ∈ (ACD). Do vậy S là một điểm chung của hai mặt phẳng (ACD) và (MNPQ). (1)
Do N ∈ AD nên N ∈ (ACD) và P ∈ CD nên P ∈ (ACD), suy ra NP ⊂ (ACD).
Mà NP ⊂ (MNPQ) nên NP là giao tuyến của hai mặt phẳng (ACD) và (MNPQ). (2)
Từ (1) và (2) suy ra S ∈ NP.
Vậy ba đường thẳng MQ, NP và AC cùng đi qua điểm S.
Lời giải:
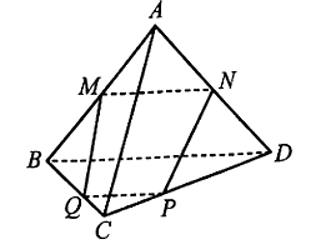
Giả sử M, N, P, Q cùng thuộc một mặt phẳng.
Vì M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác ABD, do đó MN // BD.
Do P ∈ CD nên P ∈ (BCD) và Q ∈ BC nên Q ∈ (BCD), suy ra PQ ⊂ (BCD).
Mà PQ ⊂ (MNPQ) nên PQ là giao tuyến của hai mặt phẳng (BCD) và (MNPQ).
Hai mặt phẳng (MNPQ) và (BCD) có MN // BD và PQ là giao tuyến.
Suy ra PQ // BD.
Lời giải:
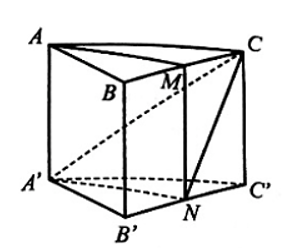
Vì M, N lần lượt là trung điểm của BC, B'C' nên MN là đường trung bình của hình thang BCC'B' (vì hình bình hành cũng là hình thang).
Suy ra MN // BB' và MN = BB'.
Mà AA' // BB' và AA' = BB' (do ABC.A'B'C' là hình lăng trụ).
Do đó, AA' // MN và AA' = MN nên AA'NM là hình bình hành.
Suy ra AM // A'N, mà A'N ⊂ (A'NC).
Vậy AM // (A'NC).
a) Chứng minh rằng SC // (MNP).
b) Xác định giao tuyến của mặt phẳng (MNP) với mặt phẳng (SCD) và giao điểm Q của đường thẳng SD với mặt phẳng (MNP).
c) Xác định giao điểm E của đường thẳng SA với mặt phẳng (MNP).
d) Tính tỉ số SESA.
Lời giải:
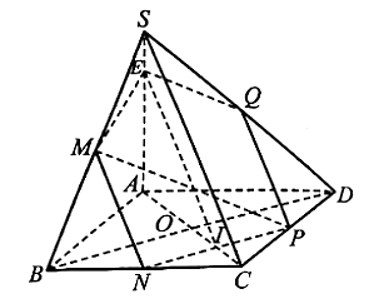
a) Vì M, N lần lượt là trung điểm của các cạnh SB, BC nên MN là đường trung bình của tam giác SBC, do đó MN // SC. Mà MN ⊂ (MNP).
Từ đó suy ra SC // (MNP).
b) Gọi Q là trung điểm của SD, mà P là trung điểm của CD nên PQ là đường trung bình của tam giác SCD nên SC // QP.
Hai mặt phẳng (MNP) và (SCD) có điểm P chung và MN // SC nên giao tuyến của hai mặt phẳng (MNP) và (SCD) là đường thẳng QP. Đồng thời, Q là giao điểm của đường thẳng SD với mặt phẳng (MNP).
c) Trong mặt phẳng (ABCD), gọi I là giao điểm của AC và NP.
Trong mặt phẳng (SAC), lấy E thuộc SA sao cho IE // SC.
Khi đó, ta có I ∈ (MNP) và IE // MN nên E ∈ (MNP).
Vậy E là giao điểm của SA với mặt phẳng (MNP).
d) Gọi O là giao điểm của AC và BD, suy ra O là trung điểm của AC và BD.
Ta có NP là đường trung bình của tam giác BCD nên NP // BD hay NI // BO.
Trong tam giác BOC có NI // BO và N là trung điểm của BC nên NI là đường trung bình của tam giác BOC, suy ra I là trung điểm của OC. Khi đó CICO=12. Suy ra CICA=14.
Xét tam giác SAC, ta có IE // SC nên SESA=CICA=14.
a) Chứng minh rằng ADC'B' là hình bình hành.
b) Chứng minh rằng BD // (AB'D'), MN // (AB'D').
c) Chứng minh rằng (MNP) // (AB'D') và BD // (MNP).
d*) Xác định giao tuyến của mặt phẳng (MNP) với các mặt của hình hộp.
e*) Lấy một đường thẳng cắt ba mặt phẳng (AB'D'), (MNP), (C'BD) lần lượt tại I, J, H. Tính tỉ số IJJH.
Lời giải:
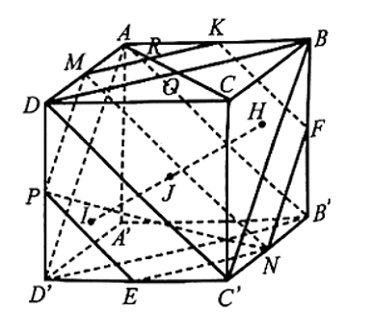
a) Vì ABCD và BCC'B' là các hình bình hành nên AD // BC, AD = BC và BC // B'C', BC = B'C'. Suy ra AD // B'C', AD = B'C'.
Vậy ADC'B' là hình bình hành.
b) Vì BB' // DD' và BB' = DD' nên BDD'B' là hình bình hành.
Do đó, BD // B'D'. Mà B'D' ⊂ (AB'D').
Suy ra BD // (AB'D').
Vì M, N lần lượt là trung điểm của AD, B'C' và AD // B'C', AD = B'C' nên AM // B'N và AM = B'N. Suy ra AMNB' là hình bình hành, do đó MN // AB'.
Mà AB' ⊂ (AB'D') nên MN // (AB'D').
c) Vì M, P lần lượt là trung điểm của AD, DD' nên MP là đường trung bình của tam giác ADD', suy ra MP // AD'. Mà AD' ⊂ (AB'D') nên MP // (AB'D').
Theo câu b ta có MN // (AB'D'). Từ đó suy ra (MNP) // (AB'D').
Vì BD // B'D' và B'D' ⊂ (AB'D') nên BD // (AB'D'), suy ra BD // (MNP).
d) Gọi E, F, K lần lượt là trung điểm của C'D', B'B, BA.
Khi đó, ta chứng minh được PE // MN, NF // MP, KF // MN nên các điểm E, F, K đều thuộc mặt phẳng (MNP).
Do đó giao tuyến của (MNP) với các mặt (ADD'A'), (DCC'D'), (A'B'C'D'), (BCC'B'), (ABB'A') và (ABCD) lần lượt là MP, PE, EN, NF, FK, KM.
e) Theo câu d, ta có mặt phẳng (MNP) trùng với mặt phẳng (MKFNEP).
Gọi R, O lần lượt là giao điểm của AC với MK, BD.
Khi đó, ta có ARRO=1 và đường thẳng AC cắt ba mặt phẳng (AB'D'), (MNP), (C'BD) lần lượt tại A, R, O. Theo giả thiết đường thẳng IJ cắt ba mặt phẳng (AB'D'), (MNP), (C'BD) lần lượt tại I, J, H. Áp dụng định lí Thalès trong không gian, ta có ARIJ=ROJH=AOIH.
Từ đó suy ra IJJH=ARRO=1.
Lời giải:
+ Hộp phấn có dạng hình hộp chữ nhật (cũng chính là hình lăng trụ), ta có hình biểu diễn nó như sau:
+ Khối rubik tam giác có dạng hình chóp, ta có hình biểu diễn của nó như sau:
Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song
Bài 4: Hai mặt phẳng song song
Bài 5: Hình lăng trụ và hình hộp
Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian




